Содержание
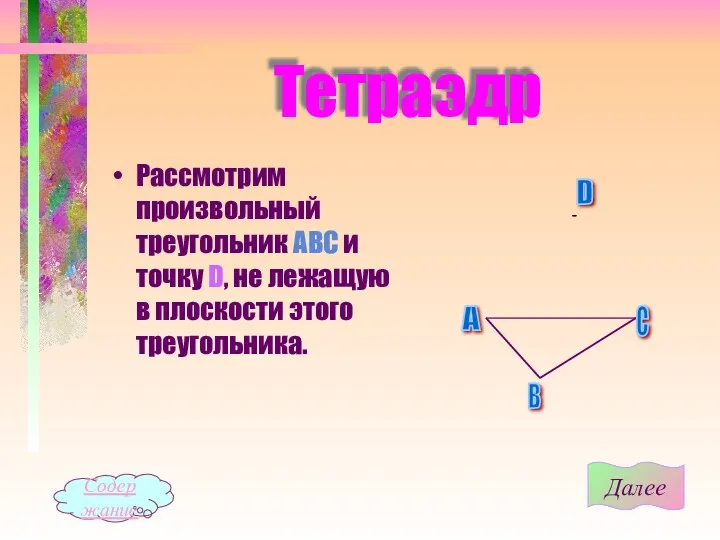
- 2. Тетраэдр Рассмотрим произвольный треугольник АВС и точку D, не лежащую в плоскости этого треугольника. Далее Содержание
- 3. Соединив точку D отрезками с вершинами треугольника АВС, получим треугольники DАВ, DВС и DСА. Содержание Далее
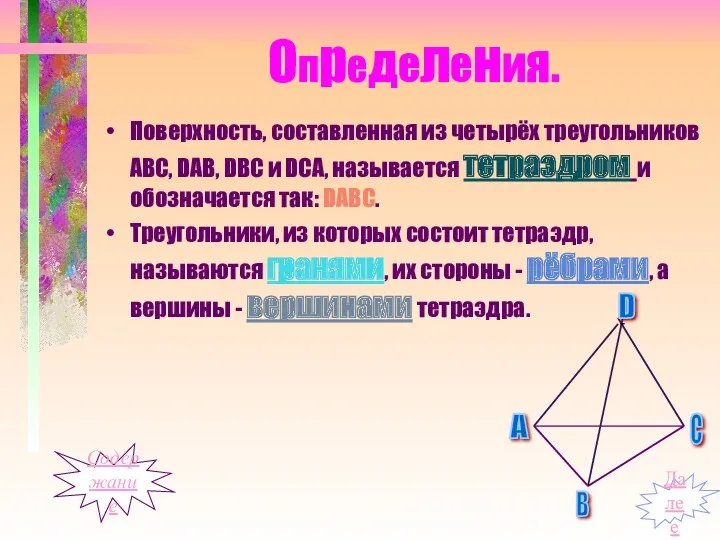
- 4. Определения. Поверхность, составленная из четырёх треугольников АВС, DАВ, DВС и DСА, называется тетраэдром и обозначается так:
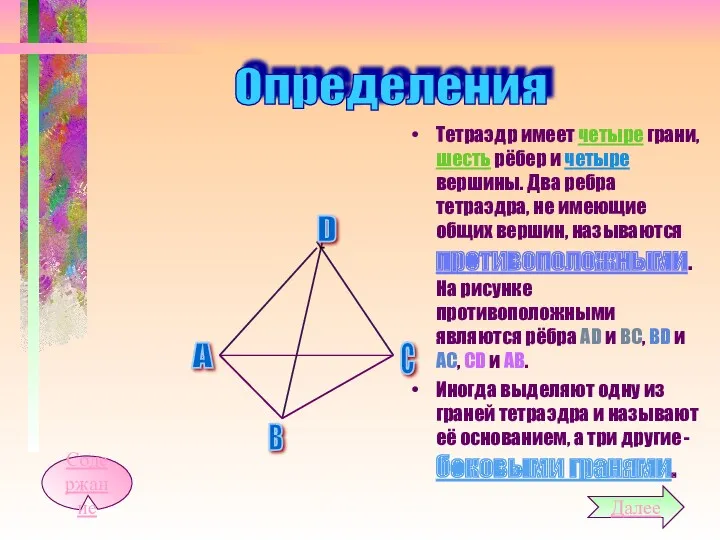
- 5. Тетраэдр имеет четыре грани, шесть рёбер и четыре вершины. Два ребра тетраэдра, не имеющие общих вершин,
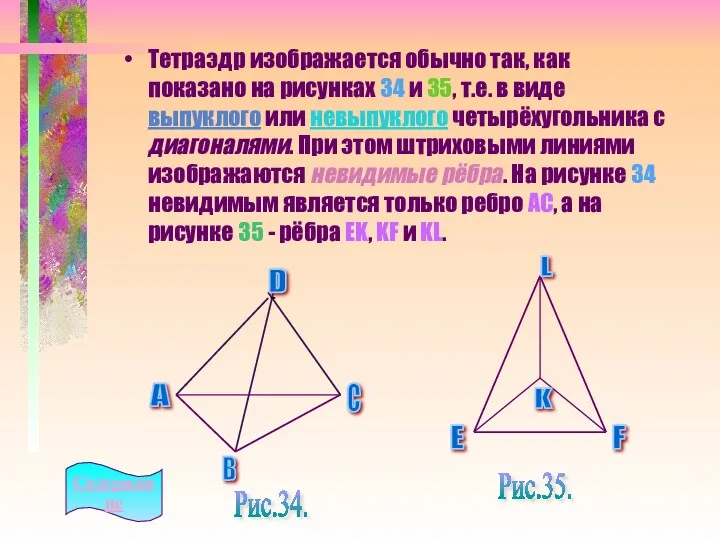
- 6. Тетраэдр изображается обычно так, как показано на рисунках 34 и 35, т.е. в виде выпуклого или
- 7. Рассмотрим два равных параллелограмма АВСD и А1В1С1D1, расположенных в параллельных плоскостях так, что отрезки АА1, ВВ1,
- 8. Тетраэдр Параллелепипед Задачи на построение сечений Выход Содержание
- 9. Четырёхугольники АВВ1А1, ВСС1В1, СDD1C1, DAA1D1 также являются параллелограммами, т.к. каждый из них имеет попарно параллельные противоположные
- 10. Поверхность, составленная из двух равных параллелограммов ABCD и A1B1C1D1 и четырёх параллелограммов, называется параллелепипедом и обозначается
- 11. Параллелепипед имеет шесть граней, двенадцать рёбер и восемь вершин. Две грани параллелепипеда, имеющие общее ребро, называются
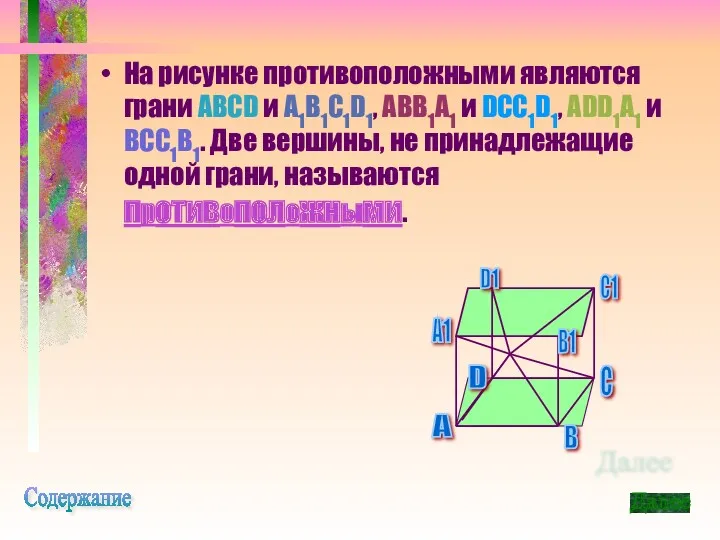
- 12. На рисунке противоположными являются грани ABCD и A1B1C1D1, ABB1A1 и DCC1D1, ADD1A1 и BCC1B1. Две вершины,
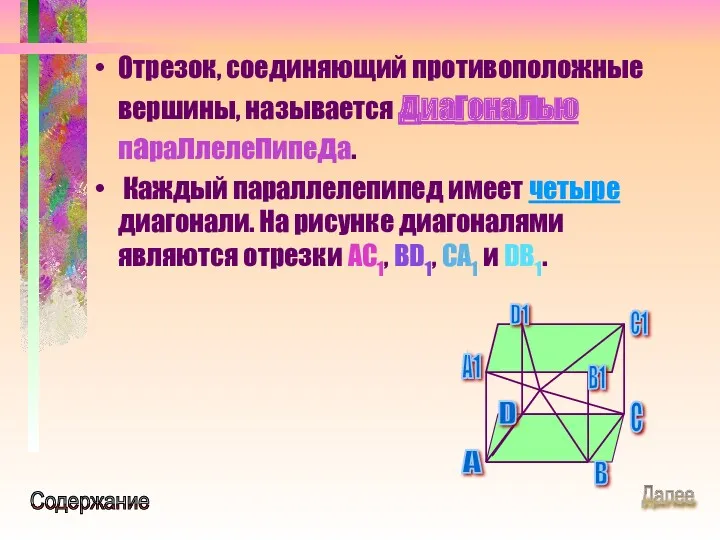
- 13. Отрезок, соединяющий противоположные вершины, называется диагональю параллелепипеда. Каждый параллелепипед имеет четыре диагонали. На рисунке диагоналями являются
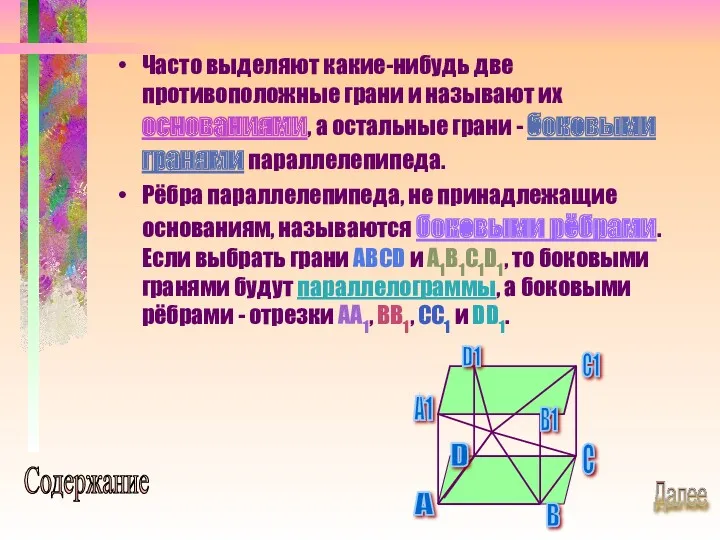
- 14. Часто выделяют какие-нибудь две противоположные грани и называют их основаниями, а остальные грани - боковыми гранями
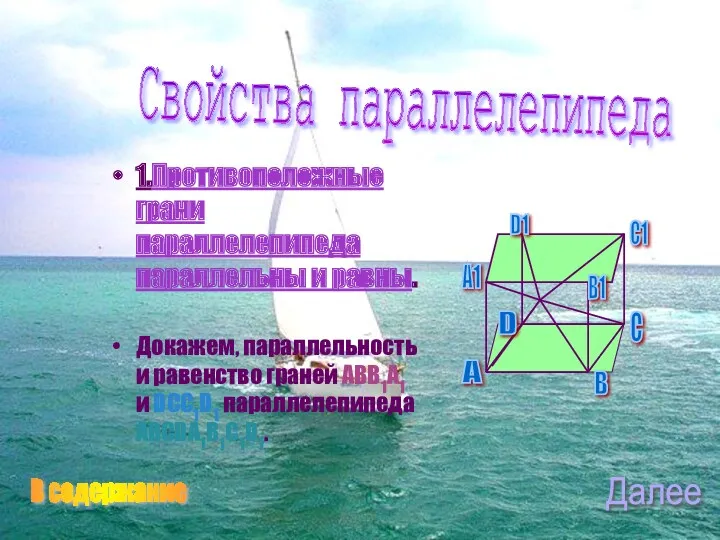
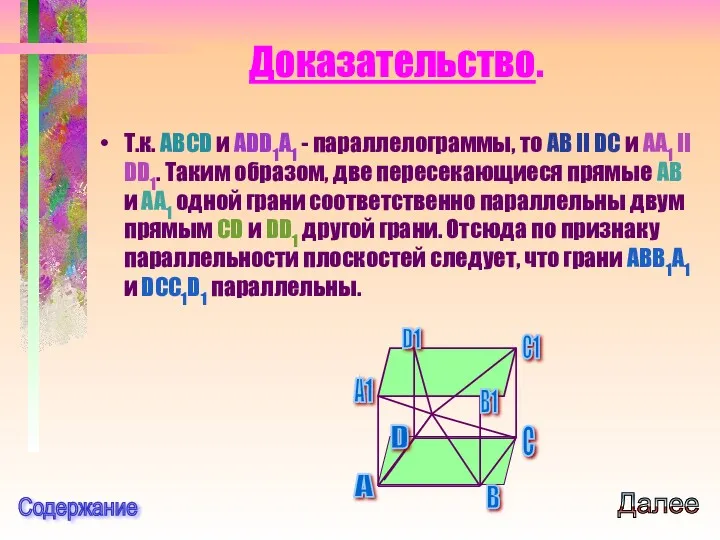
- 15. 1.Противоположные грани параллелепипеда параллельны и равны. Докажем, параллельность и равенство граней ABB1A1 и DCC1D1 параллелепипеда ABCDA1B1C1D1.
- 16. Доказательство. Т.к. ABCD и ADD1A1 - параллелограммы, то AB II DC и AA1 II DD1. Таким
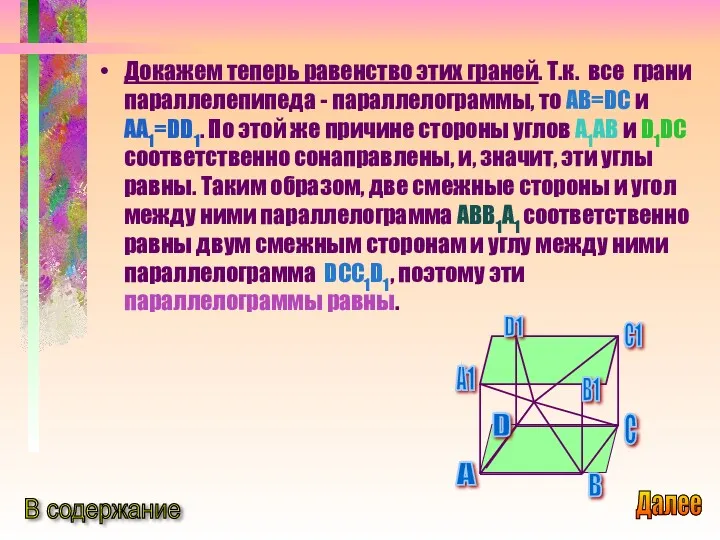
- 17. Докажем теперь равенство этих граней. Т.к. все грани параллелепипеда - параллелограммы, то AB=DC и AA1=DD1. По
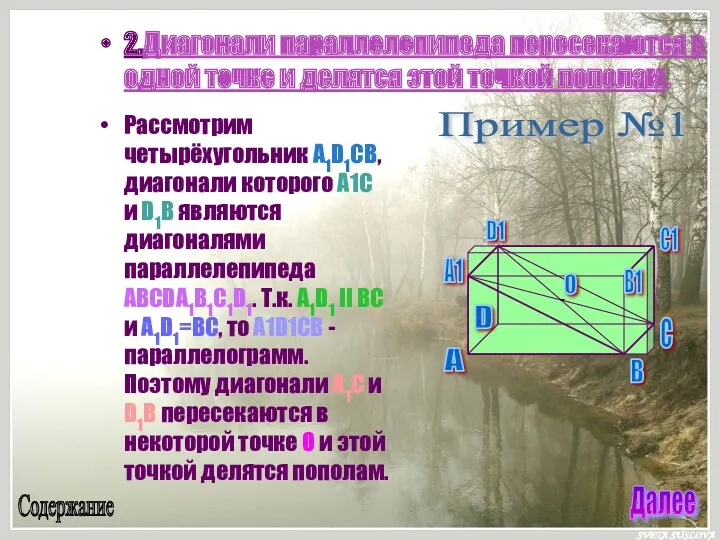
- 18. 2.Диагонали параллелепипеда пересекаются в одной точке и делятся этой точкой пополам. Рассмотрим четырёхугольник A1D1CB, диагонали которого
- 19. Рассмотрим четырёхугольник AD1C1B. Он также является параллелограммом, и, следовательно, его диагонали AC1 и D1B пересекаются и
- 20. Рассматривая четырёхугольник A1B1CD, точно так же устанавливаем, что и четвёртая диагональ DB1 параллелепипеда проходит через точку
- 21. Секущей плоскостью тетраэдра называется любая плоскость, по обе стороны от которой имеются точки данного тетраэдра (параллелепипеда).
- 22. Т.к. тетраэдр имеет четыре грани, то его сечениями могут быть только треугольники и четырёхугольники. Далее Содержание
- 23. Параллелепипед имеет шесть граней. Его сечениями могут быть треугольники, четырёхугольники (рис.39,а), пятиугольники (рис.39,б) и шестиугольники (рис.39,в).
- 24. На рисунке 39,б секущая плоскость пересекает две противоположные грани ( левую и правую) по отрезкам AB
- 25. По той же причине на рисунке 39,в AB II ED, AF II CD, BC II EF.
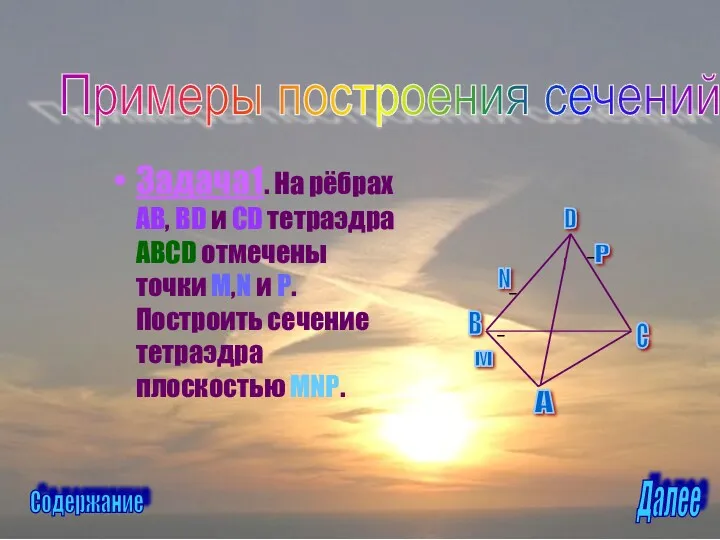
- 26. Задача1. На рёбрах AB, BD и CD тетраэдра ABCD отмечены точки M,N и P. Построить сечение
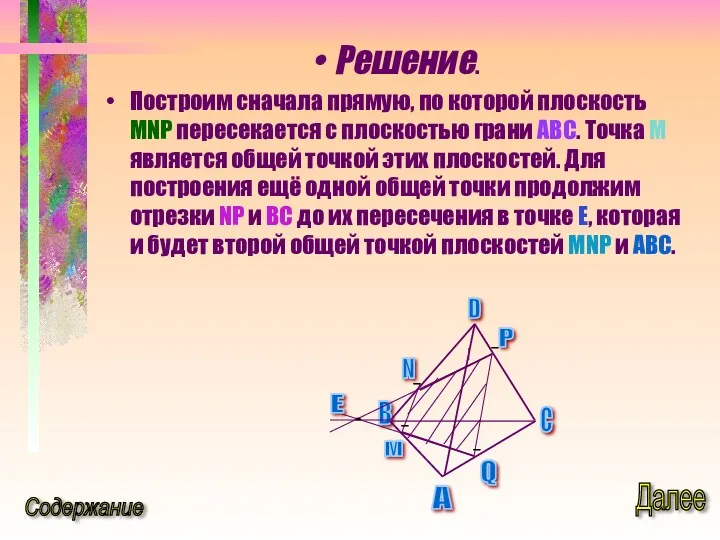
- 27. Решение. Построим сначала прямую, по которой плоскость MNP пересекается с плоскостью грани ABC. Точка М является
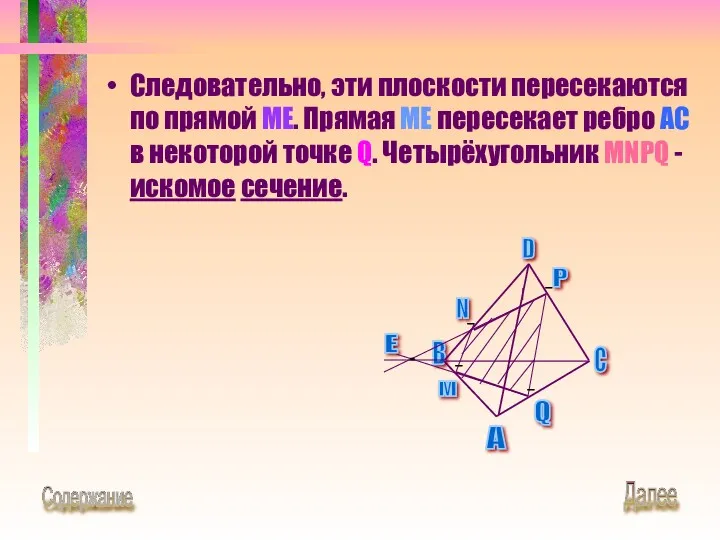
- 28. Следовательно, эти плоскости пересекаются по прямой ME. Прямая ME пересекает ребро AC в некоторой точке Q.
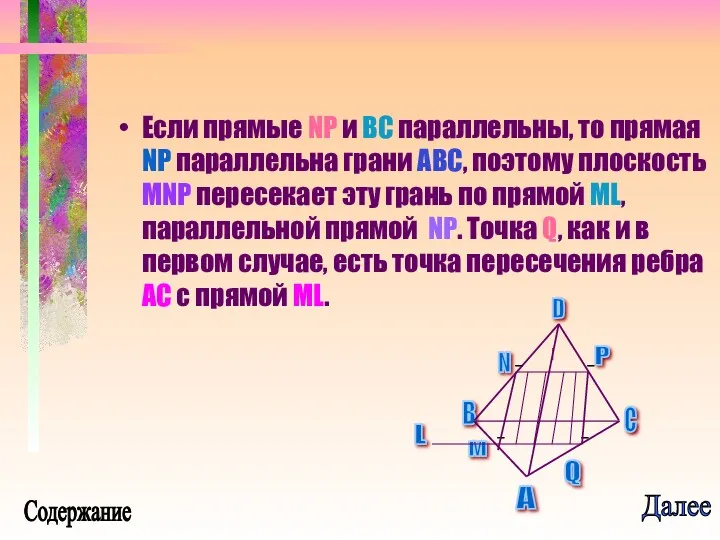
- 29. Если прямые NP и BC параллельны, то прямая NP параллельна грани ABC, поэтому плоскость MNP пересекает
- 30. Точка М лежит на боковой грани ADB тетраэдра DABC. Построить сечение тетраэдра плоскостью, проходящей через точку
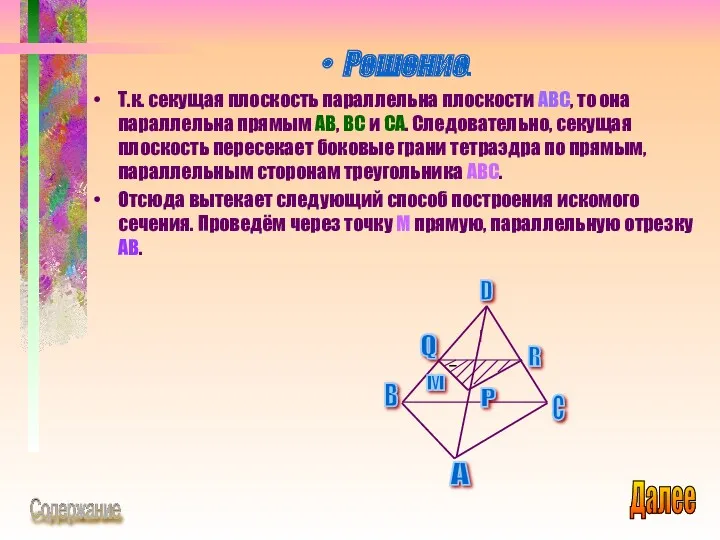
- 31. Решение. Т.к. секущая плоскость параллельна плоскости ABC, то она параллельна прямым AB, BC и CA. Следовательно,
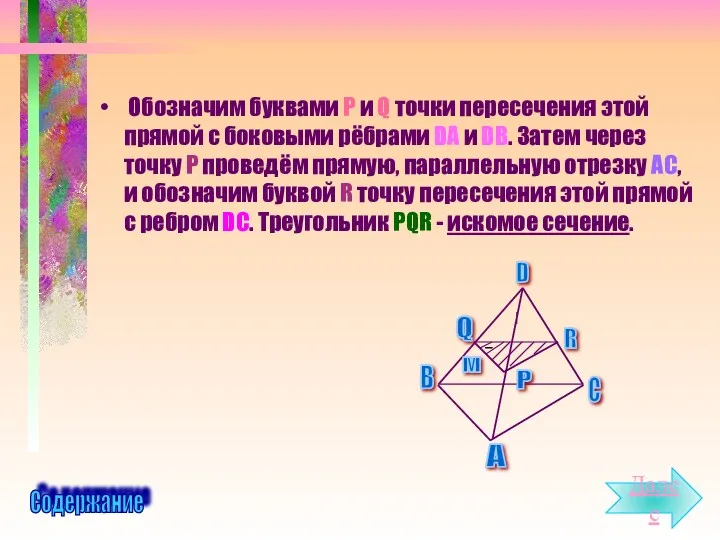
- 32. Обозначим буквами P и Q точки пересечения этой прямой с боковыми рёбрами DA и DB. Затем
- 33. На рёбрах параллелепипеда даны три точки A, B и C. Построить сечение параллелепипеда плоскостью ABC. Содержание
- 34. Решение. Построение искомого сечения зависит от того, на каких рёбрах параллелепипеда лежат точки A, B и
- 35. Если три данные точки A, B и C расположены так, как показано на рисунке, то сначала
- 36. Более трудный случай, когда данные точки A, B C расположены так, как показано на рисунке. В
- 38. Скачать презентацию


















 Начертательная геометрия. Пересечение поверхности плоскостью общего положения. (Лекция 7)
Начертательная геометрия. Пересечение поверхности плоскостью общего положения. (Лекция 7) Omówienie sprawdzianu
Omówienie sprawdzianu Уравнение множественной регрессии
Уравнение множественной регрессии Алгебра логики. Контрольная работа
Алгебра логики. Контрольная работа Измерение - нахождение значения физической величины опытным путем с помощью специальных технических средств
Измерение - нахождение значения физической величины опытным путем с помощью специальных технических средств Готовимся к ГИА
Готовимся к ГИА Плоскость. Уравнения плоскости
Плоскость. Уравнения плоскости Геометрический турнир
Геометрический турнир Треугольник и его виды
Треугольник и его виды Тесты для интерактивной доски по УМК Школа России
Тесты для интерактивной доски по УМК Школа России Математика вокруг нас. Конкурс смекалки
Математика вокруг нас. Конкурс смекалки Центральные и вписанные углы
Центральные и вписанные углы Нахождение числа по его дроби
Нахождение числа по его дроби Решение задач с помощью квадратных уравнений (по материалам Бородинского сражения)
Решение задач с помощью квадратных уравнений (по материалам Бородинского сражения) Уравнение окружности. Урок геометрии в 9 классе
Уравнение окружности. Урок геометрии в 9 классе Закономерности случайной вариации. Закон нормального распределения. Закон Гауса-Лапласа. (Лекция 3)
Закономерности случайной вариации. Закон нормального распределения. Закон Гауса-Лапласа. (Лекция 3) Формирование УУД на уроках математики
Формирование УУД на уроках математики Статистическая обработка данных. Повторение
Статистическая обработка данных. Повторение Методы и модели линейного программирования. Лекция 4
Методы и модели линейного программирования. Лекция 4 Чисельні методи (ЧМ)
Чисельні методи (ЧМ) Делимость натуральных чисел
Делимость натуральных чисел Определение показательной функции
Определение показательной функции Презентация к уроку математики 2 кл
Презентация к уроку математики 2 кл Симметрия в природе
Симметрия в природе Формулы приведения, формулы сложения. Формулы удвоения. Формулы половинного угла
Формулы приведения, формулы сложения. Формулы удвоения. Формулы половинного угла Информатика в задачах теплоэнергетики
Информатика в задачах теплоэнергетики Презентация к уроку математики Решение задач с помощью уравнения
Презентация к уроку математики Решение задач с помощью уравнения Медиа-сопровождение к уроку математики Число 9. Цифра 9
Медиа-сопровождение к уроку математики Число 9. Цифра 9