Содержание
- 2. Властивість 1. Значення визначника не змінюється при транспонуванні. Приклад 1. Наслідок. У визначнику рядки та стовпці
- 3. Властивість 3. Визначник, стовпець якого складається з нулів, дорівнює нулеві. Приклад 3 Властивість 4. Визначник, що
- 4. Властивість 5. Визначник, що має два пропорційні стовпці, дорівнює нулю. Приклад 5 Властивість 6. Визначник зросте
- 5. Властивість 7. Значення визначника не зміниться, якщо до елементів якогось стовпця додати (відняти) відповідні елементи іншого
- 6. Властивість 8. Якщо у визначнику елементи i-го рядка є сумою двох доданків, то він дорівнює сумі
- 7. Для обчислення визначників порядку використовують алгебраїчні доповнення Правило обчислення визначника n- го порядку. Мінори та алгебраїчні
- 8. Правило обчислення визначника n- го порядку. Приклад 9 Знайти алгебраїчні доповнення елементів a21 та a33 визначника
- 9. Приклад 10 Правило обчислення визначника n- го порядку. Записати алгебраічне доповненя елемента a23 визначника Розв’язок А23
- 10. Правило. Розклад визначника за елементами рядка (стовпця). (теорема Лапласа (23.03.1747-5.03.1827)). Визначник n-го порядку дорівнює сумі добутків
- 11. Обчислення визначника порядку n≥3 . Приклад 11
- 12. Обернена матриця. Матрицю А-1 називають оберненою до матриці А, якщо виконуються рівності А× А-1 = А-1×А
- 13. Обернена матриця. Знайти матрицю, обернену до матриці Приклад 12 1) Обчислюємо значення визначника матриці А Розв’язок
- 14. 3) Записуємо обернену до А матрицю Приклад 12 (продовження)
- 15. Системи лінійних рівнянь Систему алгебраїчних рівнянь називають лінійною, якщо вона може бути записана у вигляді де
- 16. Системи лінійних рівнянь Розв’язком системи називають множину дійсних чисел с1, с2, …, сn, підстановка яких у
- 17. Системи лінійних рівнянь Знаходження єдиного розв’язку Системи n лінійних рівнянь з n невідомими . С. Л.
- 18. Системи n лінійних рівнянь з n невідомими Метод Крамера. Цей визначник отримано шляхом послідовної заміни j-го
- 19. Приклад 13 Розв’язати систему лінійних рівнянь за формулами Крамера: Розв’язок ∆ ≠ 0, можемо застосувати правило
- 20. Приклад 13 (продовження) За формулами Крамера: Відповідь:
- 21. Системи n лінійних рівнянь з n невідомими Метод оберненої матриці. то С.Л. Р. , згідно з
- 22. Приклад 14 Розв’язати C.Л.Р. методом оберненої матриці Запишемо систему рівнянь у вигляді матричного рівняння Розв’язок де
- 23. Приклад 14 (продовження) Знаходимо алгебраїчні доповнення:
- 24. Приклад 14 (продовження) Запишемо обернену матрицю до матриці А
- 26. Скачать презентацию
 Рішення рівнянь
Рішення рівнянь Второй признак равенства треугольников. Решение задач
Второй признак равенства треугольников. Решение задач Моделирование химико-технологических процессов
Моделирование химико-технологических процессов Площадь многоугольника
Площадь многоугольника ВПМ. Математичне програмування та дослідження операцій. Оптимізаційні задачі управління запасами. (Лекція 5)
ВПМ. Математичне програмування та дослідження операцій. Оптимізаційні задачі управління запасами. (Лекція 5) Математическое моделирование в профессинальном образовании. Модели и моделирование. Тематика контрольных работ
Математическое моделирование в профессинальном образовании. Модели и моделирование. Тематика контрольных работ Мир чисел
Мир чисел Вписанная и описанная окружность. ОГЭ (задание № 16)
Вписанная и описанная окружность. ОГЭ (задание № 16) Фотоотчет о неделе математики
Фотоотчет о неделе математики Работа по учебнику Г.К. Муравина, О.В. Муравиной Математика 5 для общеобразовательных учреждений
Работа по учебнику Г.К. Муравина, О.В. Муравиной Математика 5 для общеобразовательных учреждений Параллельные прямые. 7 класс
Параллельные прямые. 7 класс Линейное уравнение с одной переменной
Линейное уравнение с одной переменной Великие математики древности
Великие математики древности Робота з малюнками й текстами. Розв'язування завдань для розвитку кмітливості. Урок №138
Робота з малюнками й текстами. Розв'язування завдань для розвитку кмітливості. Урок №138 Умножение и деление обыкновенной дроби на натуральное число
Умножение и деление обыкновенной дроби на натуральное число УРОК МАТЕМАТИКИ во 2 в классе ТЕМА: СЧЁТ ДЕСЯТКАМИ
УРОК МАТЕМАТИКИ во 2 в классе ТЕМА: СЧЁТ ДЕСЯТКАМИ 100 логических задач. 2 класс
100 логических задач. 2 класс Основное свойство дроби. Урок № 3. 8 класс
Основное свойство дроби. Урок № 3. 8 класс Дифференциальное исчисление функции одной переменной
Дифференциальное исчисление функции одной переменной Математический ринг
Математический ринг Особенности математического развития детей 4-5 лет
Особенности математического развития детей 4-5 лет Аксиомы стереометрии и их следствия. 10 класс
Аксиомы стереометрии и их следствия. 10 класс Площадь трапеции
Площадь трапеции Деление десятичной дроби на десятичную дробь. 5 класс
Деление десятичной дроби на десятичную дробь. 5 класс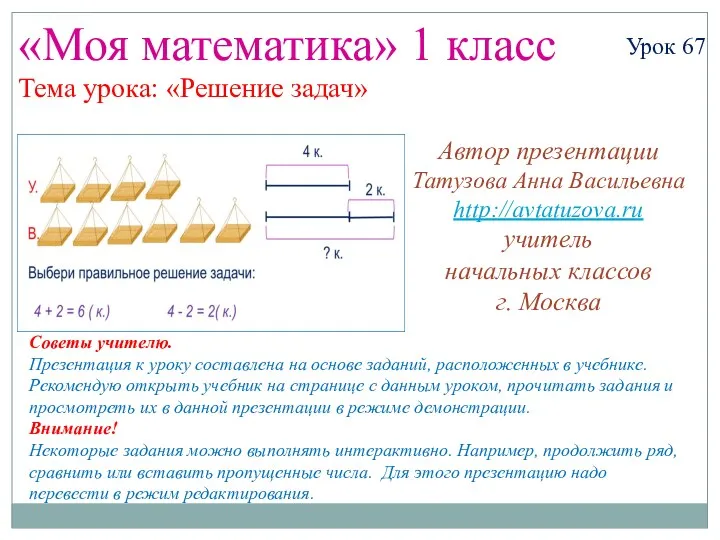 Математика. 1 класс. Урок 67. Решение задач - Презентация
Математика. 1 класс. Урок 67. Решение задач - Презентация Бинарным отношением между элементами
Бинарным отношением между элементами Урок математики
Урок математики Особенности представлений дошкольников о времени. Формирование представлений о временных понятиях.
Особенности представлений дошкольников о времени. Формирование представлений о временных понятиях.