Содержание
- 2. 1. Понятие временного ряда и его составляющих. Основная идея анализа ранее рассмо-тренных моделей заключается в том,
- 3. В реальности результирующая перемен-ная складывается под влиянием большого числа факторов, многие из которых не под-даются непосредственному
- 4. В этом случае мы имеем дело с другим видом статистических данных – временными рядами в отличие
- 5. Отдельные наблюдения этого показателя называются уровнями ряда и обозначаются символами , где число уровней ряда (число
- 6. факторы, формирующие основную тенденцию ряда (трендовая компонента); факторы, определяющие циклические колебания ряда (циклическая компонента); случайные факторы
- 7. В большинстве случаев фактический уровень временного ряда можно представить как сумму или как произведение трендовой, циклической
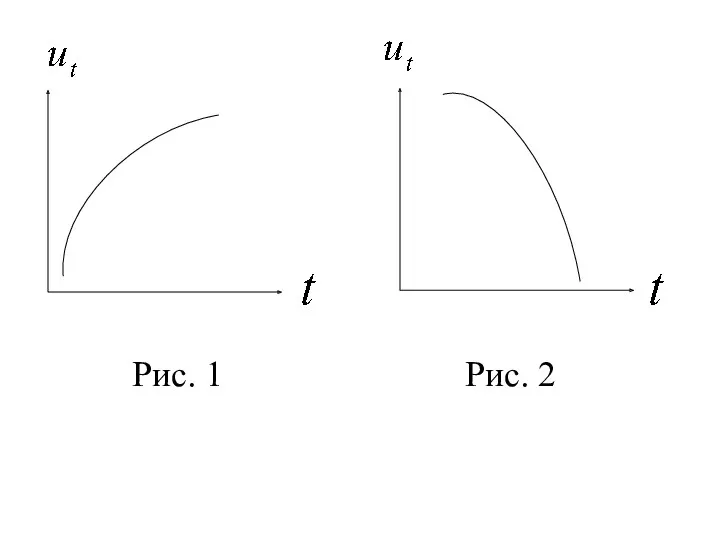
- 8. аддитивная модель ; мультипликативная модель В этих уравнениях: тренд, описывающий влияние долговременных факторов, т.е. длительную, "вековую"
- 9. Рис. 1 Рис. 2
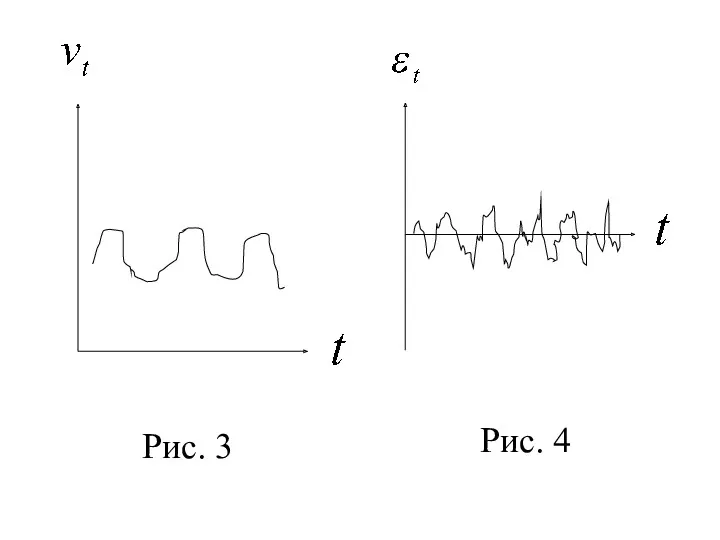
- 10. циклическая компонента, отража-ющая повторяемость экономических процес-сов. Циклические колебания могут носить сезонный характер, и связаны они с
- 11. Рис. 3 Рис. 4
- 12. случайная компонента, отражающая влияние не поддающихся регистрации случа-йных факторов (рис. 4). 2. Стационарные временные ряды. Для
- 13. Поиск адекватной модели ряда обычно начинают в рамках класса стационарных временных рядов. Ряд называется строго стационар-ным,
- 14. Ряд называется слабо стационарным (стационарным в широком смысле), если для него выполняются следующие соотношения: 1. .
- 15. Другими словами ряд слабо стационарен, если математическое ожидание, дисперсия и автоковариация ряда не зависят от времени
- 16. Автоковариация имеет те же недостатки, что и ковариация: с трудом поддаётся непо-средственной интерпретации и зависит от
- 17. Число периодов , по которым рассчи-тывается коэффициент автокорреляции, на-зывается лагом. Если , то имеем коэффициент автокорреляции
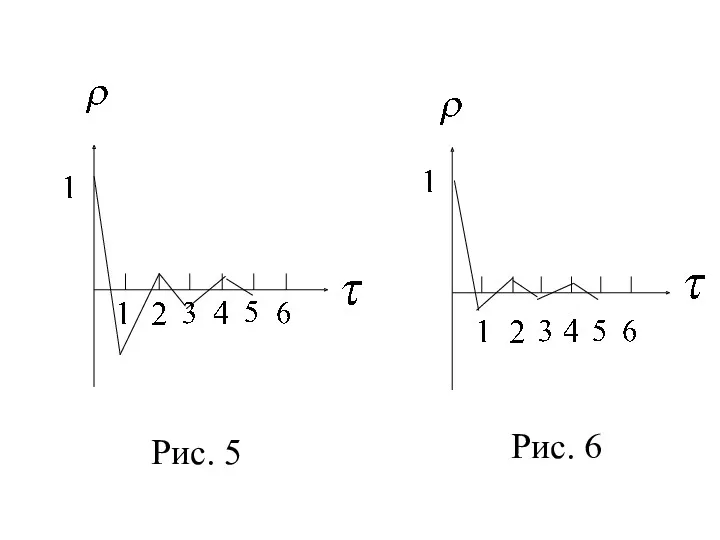
- 18. Отметим две особенности . Во-первых, он изменяется в пределах Для некоторых временных рядов, имеющих сильную нелинейную
- 19. Во-вторых, по знаку нельзя делать вывод о возрастающей или убывающей тенденции уровней ряда. Бывает так, что
- 20. Рис. 5 Рис. 6
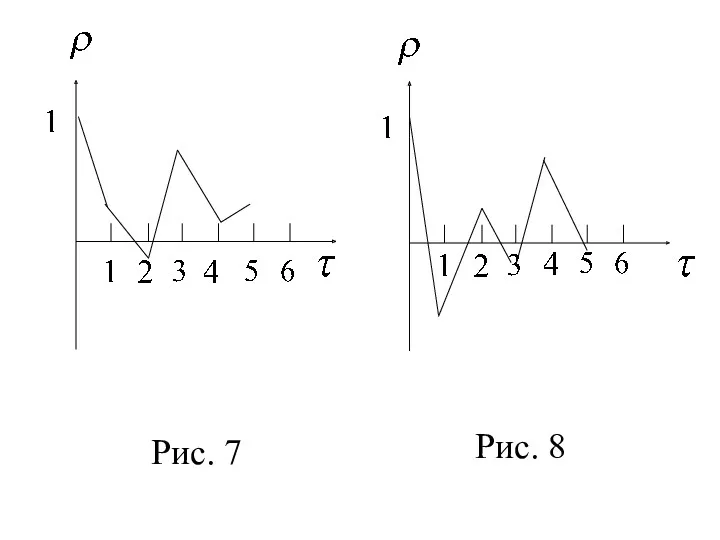
- 21. Рис. 7 Рис. 8
- 22. Анализ автокорреляционной функции и её графика помогает выявить структуру ряда. Если чередуются затухающие положи-тельные и отрицательные
- 23. Если наиболее высоким оказался коэффици-ент автокорреляции го порядка, то ряд содержит циклические колебания с пери-одичностью в
- 24. Статистическими оценками числовых характеристик слабо стационарного времен-ного ряда являются: выборочное среднее ; выборочная дисперсия
- 25. выборочный коэффициент автокор-реляции ( 1,2,3,…) Функцию переменной называют выборочной автокорреляционной функцией.
- 26. Наряду с рассматривают частные коэффициенты автокорреляции , которые характеризуют тесноту линейной связи уровней ряда и при
- 27. 3. Выравнивание временных рядов. Если при анализе структуры временного ряда обнаружена только тенденция и отсут-ствуют циклические
- 28. Для выявления основной тенденции в уровнях ряда, т.е. выравнивания ряда, ис-пользуются различные методы: механическое (алгоритмическое) выравнивание;
- 29. Если интервал содержит нечётное число уровней ряда, то среднее значе-ние ряда находится по формуле Чаще всего
- 30. Если выбранный интервал содержит чётное число уровней ряда, то вначале нахо-дятся скользящие средние для промежуточных уровней
- 31. Существуют и другие методы механического выравнивания ряда: метод взвешенных скользящих средних, метод экспоненциаль-ного сглаживания (метод Брауна),
- 32. Для этого можно использовать различ-ные виды функций: линейный тренд ; гиперболический тренд ; степенной тренд и
- 33. Параметры каждого из перечисленных трендов можно определять обычным МНК, используя в качестве независимой перемен-ной время ,
- 34. 4. Моделирование ряда при наличии циклических колебаний. Существует несколько подходов при моделировании рядов с циклическими коле-баниями.
- 35. Если амплитуда сезонных колебаний со временем не меняется, то применяют адди-тивную модель . В противном случае
- 36. в случае аддитивной модели сумма всех сезонных компонент за год должна быть равна нулю; для мультипликативной
- 37. 2. Расчет значений сезонной компоненты. Оценки сезонной компоненты находятся как разность между фактическими уровнями ряда и
- 38. В аддитивной модели сумма значений сезонной компоненты по всем сезонам должна быть равна нулю. Если это
- 39. Затем рассчитываются скорректированные значения сезонной компоненты как разность между ее средней оценкой и корректирующим коэффициентом :
- 40. Из каждого уровня исходного ряда вычитается скорректированное значение сезонной компоненты , в результате получается ряд, содержащий
- 41. 5. Расчет суммы значений трендовой и сезонной компонент К значениям выровненных уровней ряда прибавляются значения скорректированной
- 43. Скачать презентацию




































 Многомерная линейная регрессия
Многомерная линейная регрессия Урок математики по теме Свойства сложения, 2 класс
Урок математики по теме Свойства сложения, 2 класс Тройные интегралы
Тройные интегралы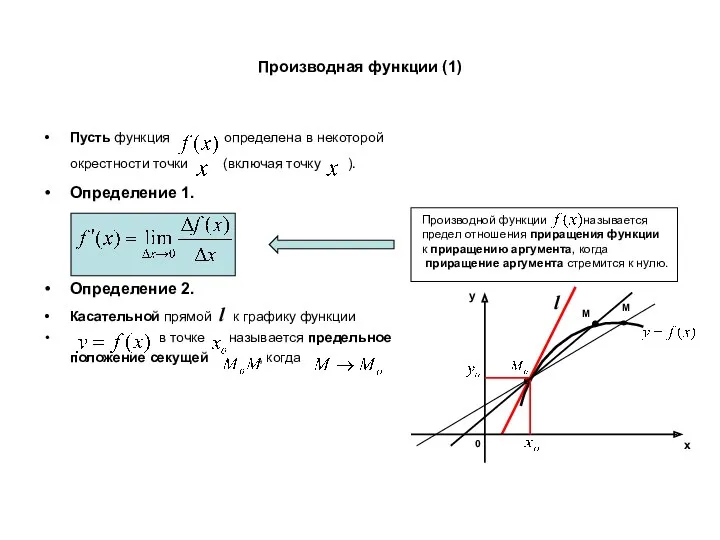 Производная функции
Производная функции Правило решения квадратных уравнений. Историческая справка
Правило решения квадратных уравнений. Историческая справка Отношения эквивалентности и порядка
Отношения эквивалентности и порядка Применение ленты Мёбиуса
Применение ленты Мёбиуса Проект по математике в 4 классе Мир в движении
Проект по математике в 4 классе Мир в движении Цилиндр. Определение цилиндра, развёртка цилиндра, формулы для вычисления
Цилиндр. Определение цилиндра, развёртка цилиндра, формулы для вычисления Давайте, посчитаем!
Давайте, посчитаем! Логикалық операциялар (дизъюнкция, конъюнкция, инверсия)
Логикалық операциялар (дизъюнкция, конъюнкция, инверсия) Методы оптимизации
Методы оптимизации Синус, косинус и тангенс острого угла прямоугольного треугольника
Синус, косинус и тангенс острого угла прямоугольного треугольника Электронный тренажёр по математике.
Электронный тренажёр по математике. Векторы. Сложение векторов
Векторы. Сложение векторов Умножение и деление обыкновенных дробей
Умножение и деление обыкновенных дробей проверка деления с остатком
проверка деления с остатком Параллельные прямые
Параллельные прямые Понятие формы. Многообразие форм окружающего мира
Понятие формы. Многообразие форм окружающего мира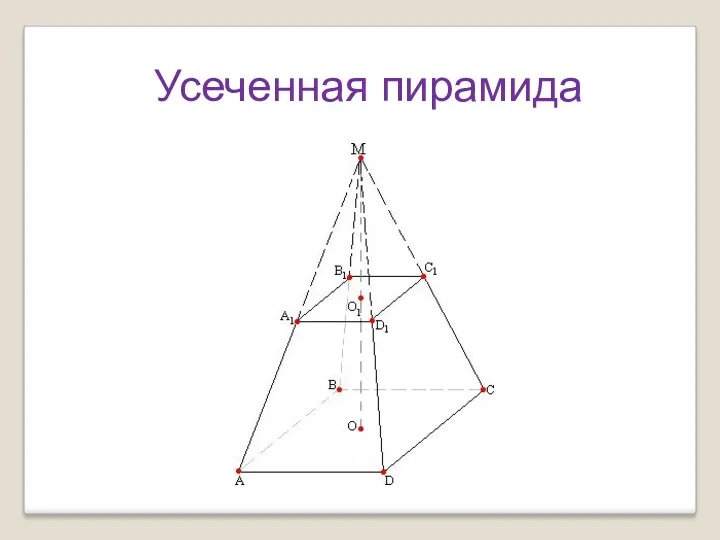 Усеченная пирамида
Усеченная пирамида Система линейных алгебраических уравнений (СЛАУ)
Система линейных алгебраических уравнений (СЛАУ) Деление дробей
Деление дробей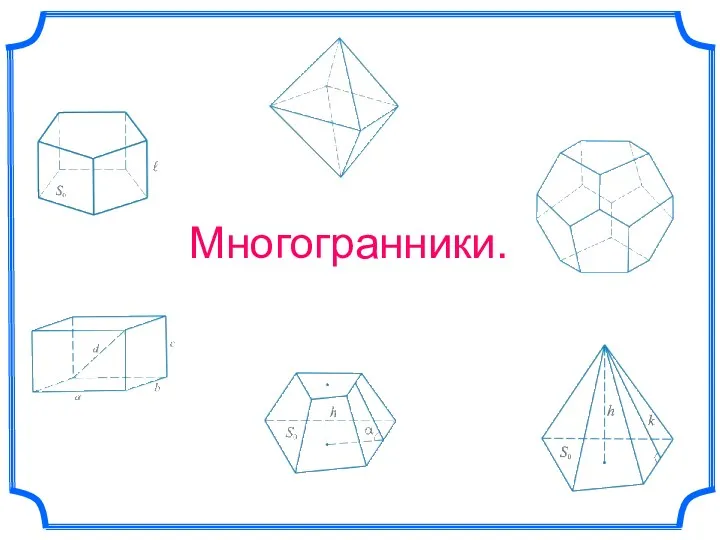 Многогранники. Выпуклые и невыпуклые многогранники
Многогранники. Выпуклые и невыпуклые многогранники Принципы симметрии
Принципы симметрии Теория вероятностей. Статистические методы обработки информации
Теория вероятностей. Статистические методы обработки информации Распознавание и называние геометрических тел: куб, шар, пирамида, цилиндр
Распознавание и называние геометрических тел: куб, шар, пирамида, цилиндр Решение уравнений. 6 класс
Решение уравнений. 6 класс Взаимное расположение графиков линейных функций
Взаимное расположение графиков линейных функций