Содержание
- 2. Коли кожному елементу x множини Х (х∈Х) ставиться у відповідність визначений елемент y множини Y (y∈Y),
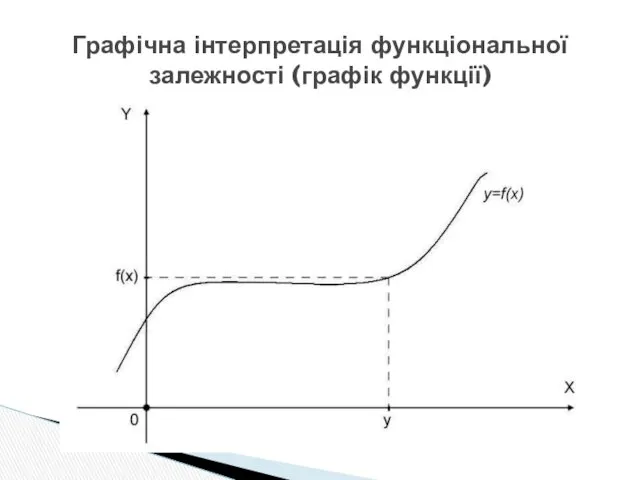
- 3. Графічна інтерпретація функціональної залежності (графік функції)
- 4. x – незалежна змінна (аргумент); X – множина визначення (існування) функції, позначається D(y); y – залежна
- 5. Функція може задаватися наступними способами: таблично (задається таблиця, в якій значенням x відповідають значення y); Приклад.
- 6. Функція може задаватися наступними способами: словесно (наприклад, функція Діріхлє: f(x)=1, якщо x – раціональне число, f(x)=0,
- 7. Можливі наступні варіанти аналітичного задання функції: а) явне задавання функції співвідношенням y=f(x); б) неявне задавання функції
- 8. в) параметричне задавання функції системою співвідношень: де t – параметр, y вважається значенням функції, що відповідає
- 9. 1. Парність та непарність. Парною називається функція y=f(x), така що для ∀x∈D(x), число (-x) також належить
- 10. 2. Монотонність. Зростаючою (спадною) називається функція, для якої на проміжку X більшому значенню аргументу відповідає більше
- 11. y=x2 для всіх х [0;∞] y=ctgx функція зростає спадає для всіх x Приклади строго монотонних функцій
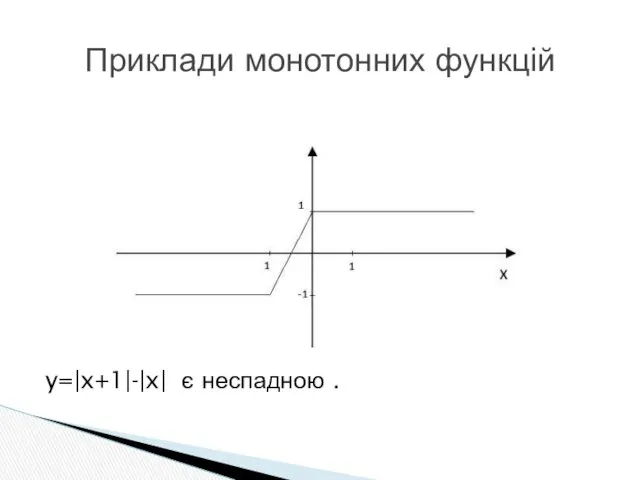
- 12. y=|x+1|-|x| є неспадною . Приклади монотонних функцій
- 13. 3. Обмеженість. Обмеженою на множині Х називається функція, для якої існує таке число М, що |f(x)|≤M
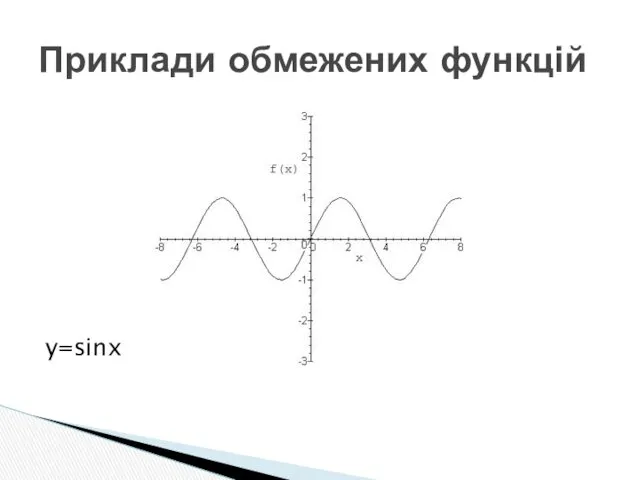
- 14. y=sinx Приклади обмежених функцій
- 15. 4. Періодичність. Періодичною називається функція, для якої існує таке число T≠0, що для довільного x∈D(x) виконується
- 16. Якщо значенню y∈E(y) ставиться у відповідність єдине x таке, що f(x)=y то отриману функцію називають оберненою
- 17. Степенева y=xa; Показникова y=ax; Логарифмічна y=logax; Гіперболічна y=a/x; Експоненційна y=ea/x; Многочлени Pn(x)=a0xn+a1xn-1+...+an ступеню n Примітка: перші
- 18. Кажуть, що задано числову послідовність, якщо кожному натуральному числу поставлене у відповідність певне дійсне число. Таким
- 19. Число a називають границею послідовності і записують , якщо для довільного числа ε>0 знайдеться такий номер
- 20. Якщо послідовність має границю, вона називається збіжною, інакше – розбіжною. Властивості збіжних послідовностей: 1) Якщо існує
- 23. Приклади
- 24. Типи невизначеностей при знаходженні границь
- 25. має місце невизначеність типу Якщо чисельник і знаменник поділити на n то звідси матимемо Приклад розкриття
- 26. має місце невизначеність типу Послідовність розбивають на дві частини. Для другої частини послідовності запишемо: Звідси маємо:
- 27. Число А називається границею функції y=f(x) при х →∞, якщо для ∀ε > 0 (наскільки завгодно
- 30. Властивості функцій, що мають границю, відповідають властивостям збіжних послідовностей. 1) Якщо функція f(x) має границю при
- 31. , оскільки х+2=3+(х-1), х-1 в цьому випадку є нескінченно малою Приклад
- 32. 4) Функція f(x) тоді і тільки тоді має границею число A, якщо для довільної послідовності чисел
- 33. 6) Границя алгебраїчної суми функцій дорівнює алгебраїчній сумі границь: Наприклад: 7) Границя добутку дорівнює добутку границь:
- 34. 8) Границя частки дорівнює частці границь: Наприклад: 9) Якщо , , то границя складеної функції Наприклад:
- 35. 10) Якщо в деякому околі точки х0 (або при достатньо великих х) виконується нерівність f(x)
- 36. Для нескінченно малих величин характерні наступні властивості: а) Алгебраїчна сума скінченної кількості нескінченно малих величин є
- 37. Першою примітною границею називається границя Її наслідками є границі: Примітні (важливі) границі
- 38. Приклади
- 39. Другою примітною границею називається границя: Наслідки такої границі
- 40. Приклад
- 41. Нескінченно малі величини називаються еквівалентними (α∼β), якщо або одного порядку малості, якщо . Якщо то α(х)називається
- 42. У випадку, коли маємо добуток, або частку нескінченно малих величин, то при знаходженні границь кожна з
- 43. З першої та другої примітних границь випливають наступні еквівалентності:
- 44. Для нескінченно великих функцій корисно використовувати еквівалентність: Рn(х) = а0хn+а1хn-1 +... + аn ~ а0хn при
- 45. Неперервною в точці х=х0 є функція y=f(x), якщо вона: а) визначена в деякому околі цієї точки;
- 46. 1) неперервність функції означає неперервність її графіка, тобто можливість зобразити його не відриваючи олівця від паперу;
- 47. Якщо функція не є неперервною в точці х0, то точка х0 називається точкою розриву функції. Розрізняють
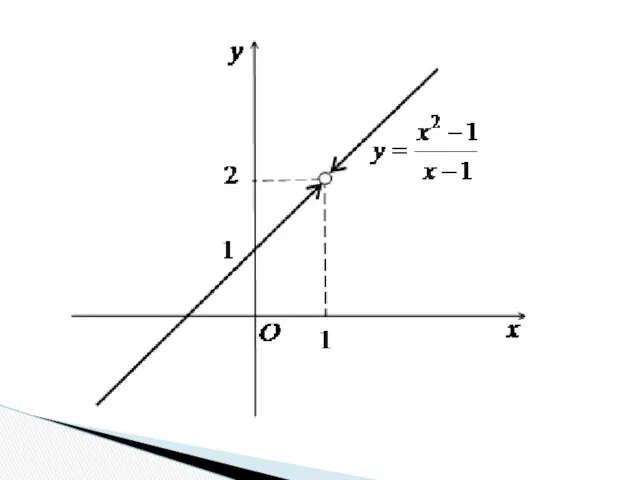
- 48. Приклад. Дослідити на розрив функцію . Розв’язання. Оскільки f(1) не існує, то x=1 - точка розриву
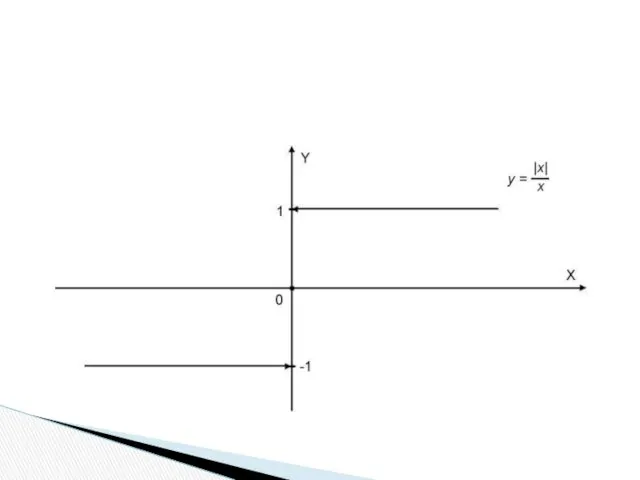
- 50. Функція має в точці x = 0 розрив першого роду («стрибок»), оскільки а значення самої функції
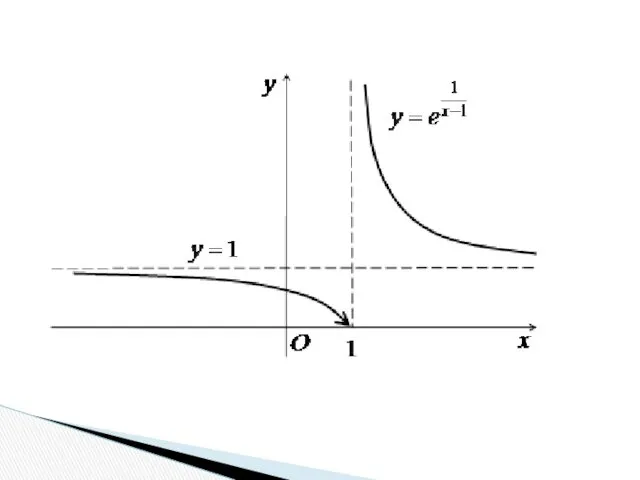
- 51. Дослідити на розрив функцію Розв’язання. Оскільки f(1) не існує, то x=1 - точка розриву функції. Обчислимо
- 53. Функції , неперервні в точці, мають наступні властивості: 1) Якщо функції f(x) та g(x) неперервні в
- 54. Всі елементарні функції неперервні в усіх точках своїх областей визначення.
- 55. Функції, неперервні на проміжку [a; b], мають наступні властивості: 1) Якщо функція y=f(x) неперервна на проміжку,
- 56. Формулою бінома Ньютона називають рівність: де, a, b – дійсні числа. n=1, 2, 3,... - натуральне
- 57. Справедливі такі співвідношення
- 58. Приклад 1. Знайти границі послідовностей. 1.1) 1.2) Приклади вирішення задач
- 59. Розв’язок задачі 1.1. Для розкриття заданої невизначеності типу {∞/∞} виносимо в чисельнику та знаменнику вищу ступінь
- 60. Розв'язання буде простішим, якщо врахувати, що
- 61. Розв’язок задачі 1.2.
- 62. Приклад 1. Приклади по розкриттю невизначеностей
- 63. Розв’язок прикладу 1.а. Підстановка граничного значення х = 1 призводить до невизначеності типу {0/0}. Розкладемо чисельник
- 65. Розв’язок прикладу 1.в. Позбудемось ірраціональності в чисельнику, помноживши чисельник і знаменник на Далі в чисельнику скористаємось
- 66. Розв’язок прикладу 1.г. Домножимо чисельник і знаменник на вирази, спряжені до чисельника і знаменника. Скориставшись відповідними
- 67. Розв’язок прикладу 1.г.
- 68. Приклад 2. Знайти границі заданих функцій.
- 69. Розв’язок прикладу 2.а.
- 70. Розв’язок прикладу 2.б.
- 71. Розв’язок прикладу 2.в.
- 72. Розв’язок прикладу 2.г.
- 74. Скачать презентацию








![y=x2 для всіх х [0;∞] y=ctgx функція зростає спадає для всіх x Приклади строго монотонних функцій](/_ipx/f_webp&q_80&fit_contain&s_1440x1080/imagesDir/jpg/88751/slide-10.jpg)






































![Функції, неперервні на проміжку [a; b], мають наступні властивості: 1)](/_ipx/f_webp&q_80&fit_contain&s_1440x1080/imagesDir/jpg/88751/slide-54.jpg)








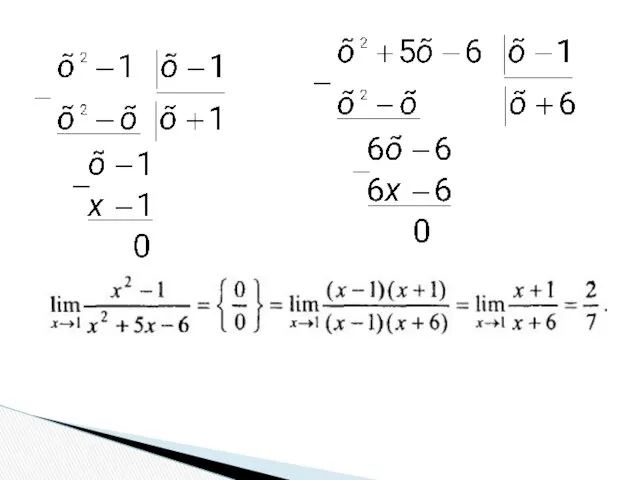








 Символы математической логики
Символы математической логики Деление с остатком
Деление с остатком Деление рациональных дробей. Урок алгебры в 8 классе
Деление рациональных дробей. Урок алгебры в 8 классе Площадь прямоугольника. К конспекту урока по математике. 5 класс
Площадь прямоугольника. К конспекту урока по математике. 5 класс Пропорции
Пропорции Элементы комбинаторики. Перестановки
Элементы комбинаторики. Перестановки Прямая призма. Решение задач
Прямая призма. Решение задач Правильные многогранники
Правильные многогранники Системы линейных уравнений
Системы линейных уравнений Физикалық дамуды бағалау үшін регрессия және корреляцияны қолдану
Физикалық дамуды бағалау үшін регрессия және корреляцияны қолдану Окружность в планиметрических задачах повышенного уровня ОГЭ и ЕГЭ
Окружность в планиметрических задачах повышенного уровня ОГЭ и ЕГЭ Математика вокруг нас
Математика вокруг нас Углы. Виды углов
Углы. Виды углов Квадратный корень из дроби
Квадратный корень из дроби Метрология и теория измерений. Метрологические характеристики средств измерений. (Лекция 7)
Метрология и теория измерений. Метрологические характеристики средств измерений. (Лекция 7) Игра для урока математики
Игра для урока математики Конкретный смысл действия умножения. Устный счёт
Конкретный смысл действия умножения. Устный счёт Интегрированный урок: математика + биология. Простые и сложные листья
Интегрированный урок: математика + биология. Простые и сложные листья Джон Непер
Джон Непер Расстояние между точками координатной прямой
Расстояние между точками координатной прямой Презентация Путешествие в страну дробей
Презентация Путешествие в страну дробей Тест. Задания В1, ЕГЭ по математике
Тест. Задания В1, ЕГЭ по математике Делимость чисел
Делимость чисел Письменные приемы вычеслений 4 класс (Рудницкая В.Н.)
Письменные приемы вычеслений 4 класс (Рудницкая В.Н.)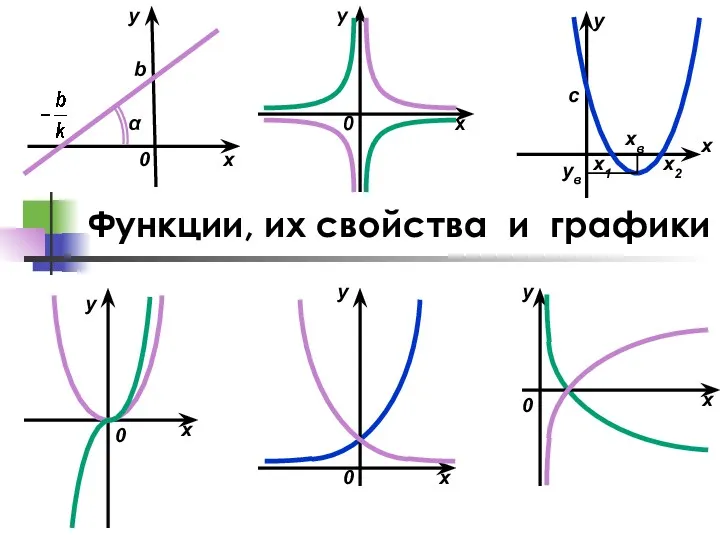 Функции, их свойства и графики
Функции, их свойства и графики Прямоугольник. Ось симметрии фигуры
Прямоугольник. Ось симметрии фигуры Нумерація чисел першої сотні. Нумераційна таблиця. Знаходження невідомого доданка. Урок №106
Нумерація чисел першої сотні. Нумераційна таблиця. Знаходження невідомого доданка. Урок №106 Умножение и деление обыкновенной дроби на натуральное число
Умножение и деление обыкновенной дроби на натуральное число