Содержание
- 2. Воспользуемся формулой где m – любое действительное число. В нашем случае: бинома Ньютона:
- 4. Видно, что с ростом n увеличивается число положительных слагаемых, которых всего будет n+1, и растет величина
- 5. Теперь каждую дробь в правой части заменяем большей дробью с двойкой в знаменателе: Получаем:
- 6. Сумма есть сумма n-1 членов геометрической прогрессии, где первый член и знаменатель По формуле суммы членов
- 7. Т.к. Sn-1 Действительно, данная последовательность является ограниченной.
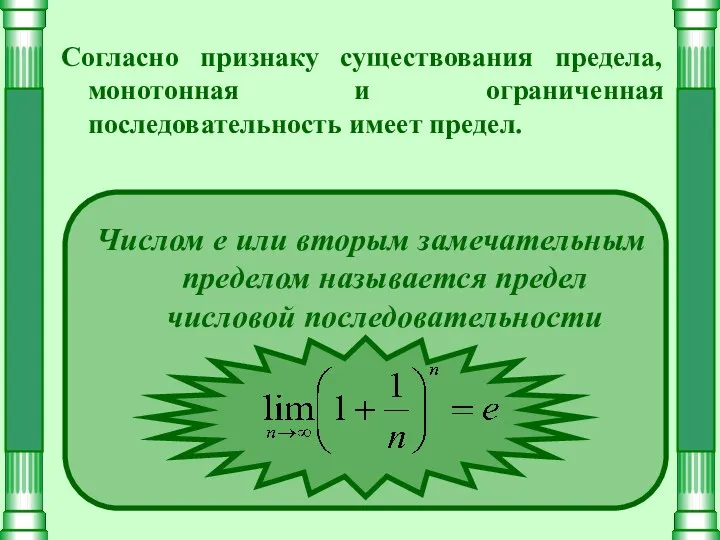
- 8. Согласно признаку существования предела, монотонная и ограниченная последовательность имеет предел. Числом е или вторым замечательным пределом
- 9. е – число Эйлера е=2,718281… Можно показать, что функция при где х пробегает все значения, а
- 10. Второй замечательный предел
- 11. Пусть , тогда Второй замечательный предел
- 12. Примеры. 1 Вычислить
- 13. Решение:
- 14. 2 Вычислить
- 15. Решение:
- 16. 3 В качестве еще одного примера рассмотрим задачу о непрерывном начислении процентов. Первоначальный вклад в банк
- 17. То есть На практике часто применяются сложные проценты. В этом случае размер вклада ежегодно будет увеличиваться
- 18. Если начислять проценты не один, а n раз в году, то при ежегодном приросте Р %,
- 19. Будем полагать, что проценты по вкладу начисляются каждое полугодие (n=2), ежеквартально (n=4), ежемесячно (n=12), каждый день
- 21. Скачать презентацию

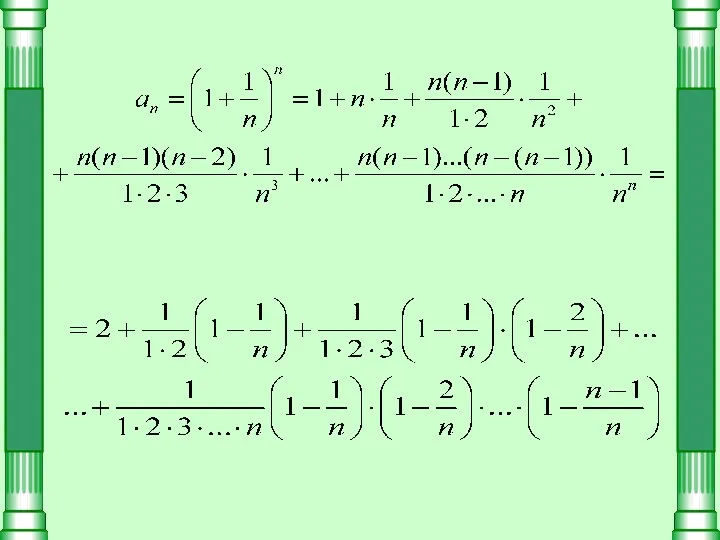



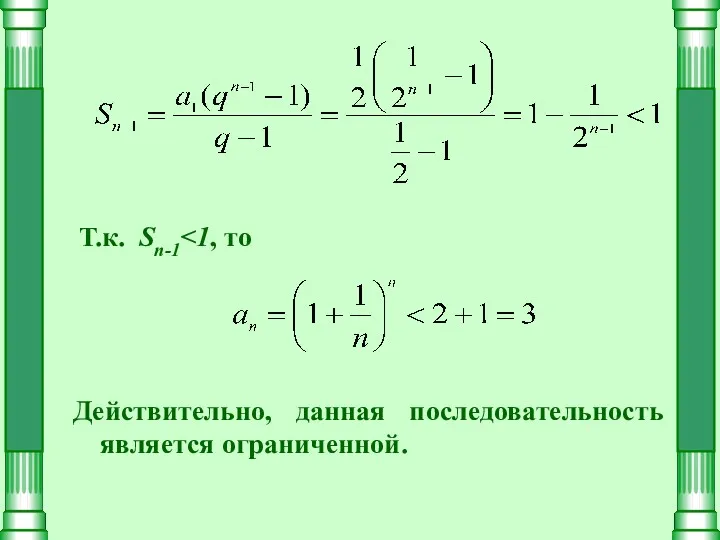











 Вычитание удобным способом
Вычитание удобным способом Признаки деления на 3, на 9
Признаки деления на 3, на 9 Физкультминутка(презентация)
Физкультминутка(презентация) Транспортная задача
Транспортная задача Некоторые свойства прямоугольного треугольника. Урок 47
Некоторые свойства прямоугольного треугольника. Урок 47 Равные треугольники. Высота, биссектриса, медиана. 7 класс
Равные треугольники. Высота, биссектриса, медиана. 7 класс Формулы сокращенного умножения
Формулы сокращенного умножения устный счет
устный счет Сумматор
Сумматор Презентация Ох, уж эта математика
Презентация Ох, уж эта математика Свойства функции. 10 класс
Свойства функции. 10 класс Геометрический смысл производной. Подготовка к ЕГЭ
Геометрический смысл производной. Подготовка к ЕГЭ Сложение и вычитание в пределах 20
Сложение и вычитание в пределах 20 Счастливый случай. Игра
Счастливый случай. Игра Инновационный опыт
Инновационный опыт Задачи на нахождение значений параметра
Задачи на нахождение значений параметра Урок Чему я научился: умножать и делить во 2 классе. Обобщающий урок по математике, УМК Перспектива.
Урок Чему я научился: умножать и делить во 2 классе. Обобщающий урок по математике, УМК Перспектива. Прямоугольная система координат на плоскости. 6 класс
Прямоугольная система координат на плоскости. 6 класс Ряд натуральных чисел
Ряд натуральных чисел Многогранники и их виды
Многогранники и их виды Понятие движения в геометрии
Понятие движения в геометрии Системы двух уравнений с двумя неизвестными. 7 класс
Системы двух уравнений с двумя неизвестными. 7 класс Треугольники. Виды треугольников. Основные свойства треугольников
Треугольники. Виды треугольников. Основные свойства треугольников Decimals
Decimals Взаимно простые числа. Признак делимости на произведение
Взаимно простые числа. Признак делимости на произведение Сложение и вычитание векторов
Сложение и вычитание векторов устный счёт в виде теста 2 класс Табличное умножение
устный счёт в виде теста 2 класс Табличное умножение Перпендикулярные прямые. Решение задач
Перпендикулярные прямые. Решение задач