Содержание
- 2. Функцией называется правило, по которому каждому элементу X некоторого множества K соответствует единственный элемент Y другого
- 3. Окрестностью точки x0 на числовой прямой называется любой интервал (a;b), содержащий эту точку. Внешность любого интервала
- 4. Односторонние пределы. Любой интервал (a-δ,a) называется левой окрестностью точки a. Любой интервал (a, a+δ) называется правой
- 5. Свойства бесконечно малых и бесконечно больших функций. Свойства бесконечно малой функции Сумма конечного числа бесконечно малой
- 6. Теоремы о связи бесконечно малой и бесконечно большой функций. Если α(x) – бесконечно малая при x→a,
- 7. Теоремы о пределах Теорема 1. Если f(x)=C=const, то Теорема 2. Теорема 3. ,если B≠0. Теорема 4.
- 8. Теорема 6. Если , то Теорема 7. (О сжатой переменной). Если функция удовлетворяет неравенству φ(x)≤f(x)≤Ф(x) и
- 9. Теорема 1. α(x) – бесконечно малая при x→a. Теорема 2.Можно показать, что решения , где α(x)
- 10. , если a=e, то . Теорема 4. , если a=e, то Теорема 3.
- 11. Сравнение бесконечно малых величин. Две бесконечно малые α(x) и β(x) при x→a называются эквивалентными при x→a,
- 12. Говорят, что при x→a порядок бесконечно малой β(x) выше порядка бесконечно малой α(x) при x→a (
- 13. Непрерывность функции. Приращение функции. Непрерывные функции.
- 14. Приращением некоторой переменной величины называется разность между новым значением этой величины и её прежним значением, т.е.
- 15. Теоремы о непрерывных функциях. 1.Основные элементарные функции непрерывны в области определения. 2.Сумма конечного числа непрерывных функций
- 16. Классификация точек разрыва. Точка, в которой нарушается непрерывность функции, называется точкой разрыва этой функции. Функция разрывна
- 17. Производная функции
- 18. Понятие производной функции в точке х0 Производной функции в точке х0 называется , если этот предел
- 19. Производная сложной функции. Пусть и . Тогда Теорема:Если функция имеет производную в точке х, а функция
- 20. 1) , где 2) 3) 4) 5) 6) , где n – натуральное число , где
- 21. Производная функции, заданной неявно. Функция вида называется функцией заданной неявно, т. е. y не выражено (х
- 22. Теорема Лагранжа о конечном приращении функции. Пусть функция непрерывна на отрезке и дифференцируема в интервале .
- 23. Необходимый и достаточный признак монотонности функции. Интервал, на котором функция возрастает или убывает, называется интервалом монотонности
- 24. Необходимое условие существования экстремума функции. Если дифференцируемая в точке c функция имеет в этой точке экстремум,
- 25. Вертикальные и невертикальные асимптоты графика функции. Асимптотой графика функции текущей точки графика функции стремится к нулю
- 27. Скачать презентацию






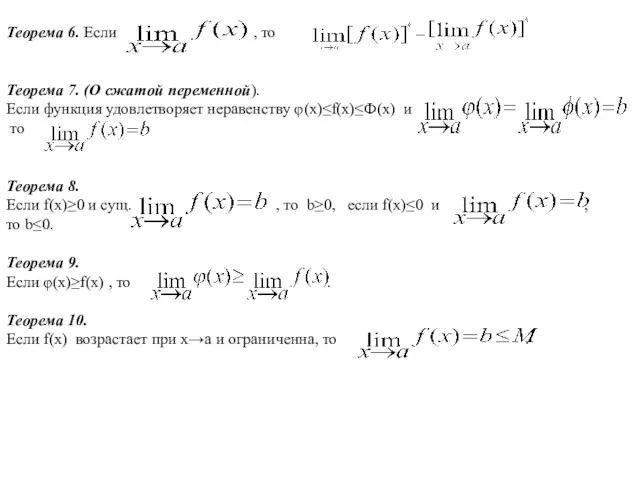

















 Фракталы в музыке
Фракталы в музыке время,скорость, расстояние
время,скорость, расстояние Разработка и проведение дидактических игр на материале заданий ОГЭ по математике
Разработка и проведение дидактических игр на материале заданий ОГЭ по математике Марковские системы массового обслуживания
Марковские системы массового обслуживания Векторная алгебра. Векторы на плоскости и в пространстве
Векторная алгебра. Векторы на плоскости и в пространстве Корень n-й степени
Корень n-й степени Параллельные плоскости и их свойства
Параллельные плоскости и их свойства Повторення вивченого. Додаткові вправи. Урок №136
Повторення вивченого. Додаткові вправи. Урок №136 Системы уравнений второй степени
Системы уравнений второй степени Квадрат түбірі бар өрнектерді түрлендіру
Квадрат түбірі бар өрнектерді түрлендіру Урок-путешествие: Галактика- математика.
Урок-путешествие: Галактика- математика. Производная в технике, физике и химии
Производная в технике, физике и химии Прямоугольные треугольники и некоторые их свойства
Прямоугольные треугольники и некоторые их свойства Величина угла. Измерение углов
Величина угла. Измерение углов Обработка результатов измерений
Обработка результатов измерений Фаррахов Динар, 7 в, (необычные способы вычислений )
Фаррахов Динар, 7 в, (необычные способы вычислений ) Царстве математики. 6 класс
Царстве математики. 6 класс Узагальнення і систематизація вивченого. Урок №131. Математика
Узагальнення і систематизація вивченого. Урок №131. Математика Разработка урока математики во 2 классе с использованием ИКТ
Разработка урока математики во 2 классе с использованием ИКТ Решение уравнений. Раскройте скобки
Решение уравнений. Раскройте скобки Сложение и умножение вероятностей
Сложение и умножение вероятностей Урок математики в 1 класс по теме Сложение с нулем дидактическая система Л.В.Занкова
Урок математики в 1 класс по теме Сложение с нулем дидактическая система Л.В.Занкова Мультимедийный урок математики по теме Периметр многоугольника
Мультимедийный урок математики по теме Периметр многоугольника Математическая статистика
Математическая статистика Блеф клуб. Математическая игра для учащихся 7-х классов
Блеф клуб. Математическая игра для учащихся 7-х классов Программа элективного курса. Тема: “Мир, математика, математики”
Программа элективного курса. Тема: “Мир, математика, математики” Решение задач на составление уравнений
Решение задач на составление уравнений Приемы сравнения чисел
Приемы сравнения чисел