Выбор нескольких элементов презентация

Пример 1.
В чемпионате участвовали 7 команд. Каждая команда играла один матч с каждой. Сколько всего было встреч?
Решение :
Рассмотрим таблицу результатов встреч размером 7x7.
Так как никакая команда не играет сама с собой, то клетки по диагонали надо закрасить. Тогда в подсчете числа встреч будет участвовать ровно
72 - 7 = 7(7 - 1) = 42 клетки.

В результате закрашивания таблица разделилась на две половинки, в них результаты встреч команд дублируются. Поэтому если мы разделим оставшиеся 42 клетки на две равные половины, то получим число всех проведенных игр.
Важно при этом то, что порядок выбора не имеет значения, т. е. если выбраны две команды, то какая из них первая, а какая вторая – не важно.

Теорема о выборках двух элементов
Если множество состоит из п элементов, то у него имеется подмножеств, состоящих из двух элементов.
Иными словами, если множество состоит из п элементов и требуется выбрать из них два элемента без учета их порядка, то такой выбор можно произвести способами.

Пример 2
В классе 27 учеников. К доске нужно вызвать двоих. Сколькими способами это можно сделать, если: а) первый ученик должен решить задачу по алгебре, а второй – по геометрии; б) они должны быстро стереть с доски?
Решение:
Для стирания с доски порядок вызова учеников не важен. А вот в первом случае порядок существенен. Тут применимо правило умножения. Учитель сначала вызывает решать алгебраическую задачу одного из 27 учеников, а затем независимым образом вызывает одного из оставшихся 26 учеников решать задачу по геометрии. Получается 27 • 26 = 702 способа вызова.
Если во втором случае начать считать, как и в первом, то любую пару учеников мы посчитаем дважды. Например, сначала Коля, потом Катя, или сначала Катя, потом Коля. Значит, количество вызовов без учета порядка будет ровно в два раза меньше, чем количество вызовов с учетом порядка.
Ответ: а) 702; 6) 351.

Всегда количество выборок двух элементов без учета порядка будет ровно в два раза меньше, чем количество выборок с учетом порядка. На рисунке представлена соответствующая схема.
Число всех выборок из n данных без учета порядка обозначается и называется числом сочетаний из n элементов по 2.

Где - количество комбинаций из n элементов по m.

Пример 3.
В классе 27 учеников, из которых нужно выбрать троих. Сколькими способами это можно сделать, если: а) первый ученик должен решить задачу, второй – сходить за мелом, третий – пойти дежурить в столовую;
б) им следует спеть хором?
а) (важен порядок вызова учеников)
б)
(порядок не важен)
Ответ. а)17550; б) 2925

Пример 4.
«Проказница Мартышка, Осел, Козел и косолапый Мишка затеяли сыграть квартет». Мишке поручили принести со склада 8 каких-нибудь попавшихся под лапы музыкальных инструментов из имеющихся 13 инструментов. Сколько способов выбора есть у Мишки?

Биномиальные коэффициенты
В математике биномиальные коэффициенты — это коэффициенты в разложении бинома Ньютона по степеням x. Коэффициент при обозначается или и читается «биномиальный коэффициент из n по k» (или «це из n по k»):
причём n здесь может быть как целым, так и произвольным действительным числом. Для неотрицательных целых n все коэффициенты с индексами k>n в этом ряду являются нулевыми, и поэтому данное разложение представляет собой конечную сумму

Значение биномиального коэффициента определено для всех действительных чисел n и целых чисел k по формулам:
где обозначает факториал числа m.
Факториа́л числа n — произведение всех натуральных чисел от 1 до n включительно:

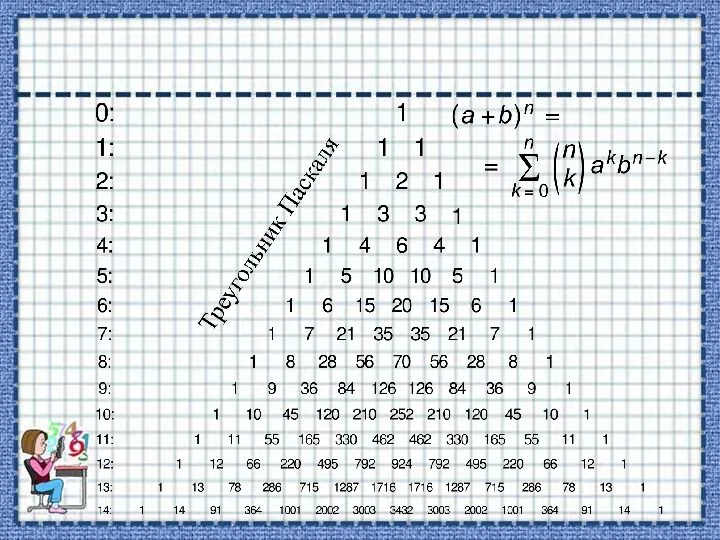
Для неотрицательных целых n и k также справедливы формулы:
Треугольник Паскаля
Треугольник Паскаля — бесконечная таблица биномиальных коэффициентов, имеющая треугольную форму. В этом треугольнике на вершине и по бокам стоят единицы. Каждое число равно сумме двух расположенных над ним чисел. Строки треугольника симметричны относительно вертикальной оси. Назван в честь Блеза Паскаля. Числа, составляющие треугольник Паскаля, возникают естественным образом в алгебре, комбинаторике, теории вероятностей, математическом анализе, теории чисел.

Числа треугольника симметричны (равны) относительно вертикальной оси.
В строке с номером n:
первое и последнее числа равны 1.
второе и предпоследнее числа равны n.
третье число равно треугольному числу , что также равно сумме номеров предшествующих строк.
четвёртое число является тетраэдрическим.
m-е число (при нумерации с 0) равно биномиальному коэффициенту

Правило записи треугольника легко запомнить. Каждое число в треугольнике паскаля равно сумме двух чисел, стоящих над ними в предыдущей строке. Давайте распишем несколько строк:

Вспомним некоторые формулы сокращенного умножения
– формула квадрата суммы. Рассмотрим, как вывести эту формулу.
раскрываем скобки, перемножая почленно:
Аналогично, для куба суммы

Выпишем для наглядности все наши формулы:
Проведем небольшой анализ полученных формул.
Обратить внимание: показатель степени в левой части равен сумме показателей степеней в правой части для любого слагаемого.
Для четвертой степени, очевидно, что слева показатель равен 4. В правой части показатель степени при первом слагаемом равен для а четырем, для b нулю и в сумме равен 4.
Для второго слагаемого сумма показателей равна 3+1=4, для следующего - 2+2=4и так до самого конца сумма показателей равна 4.

Эти два замечательных свойства, замеченных выше, позволяют вычислять сумму двух одночленов в n-ой степени:
Попробуем доказать формулу:
Рассмотрим слагаемое, стоящее на месте под номером k+1. По написанной выше формуле получаем, вот такое слагаемое:
Нам нужно доказать, что коэффициент при данном одночлене как раз и равен
Для того, чтобы двучлен возвести в n-ую степень нам нужно этот двучлен умножить на себя n раз, то есть:

Чтобы получить требуемое слагаемое надо выбрать k штук множителей для b. Тогда получается n−k множителей для а. В каком порядке будем выбирать данные множители не важно. Эта задача есть ни что иное как: число сочетаний из n элементов по k без повторений или
Наша формула доказана.
Полученная нами формула называется "Бином Ньютона".
Коэффициенты, стоящие перед слагаемыми, это биномиальные коэффициенты.