Содержание
- 2. Таким образом, Заменив нецентрированную величину X на центрированную получим Пример. Определим вероятность, что случайная величина примет
- 3. Теорема Чебышева. (12.2) Доказательство. Рассмотрим величину Определим числовые характеристики Y (см. (11.5), (11.7)):
- 4. Запишем неравенство Чебышева для величины Y: . Переходя к противоположному событию т.е. Y сходится по вероятности
- 5. где m - число опытов в которых произошло событие А; n - число проведенных опытов. Пусть
- 6. Центральная предельная теорема (12.4) Доказательство. Согласно свойству (7.16) характеристическая функция суммы равна произведению характеристических функций слагаемых:
- 7. Разложим функцию в окрестности точки t= 0 в ряд Маклорена с тремя членами: (12.6) где производные
- 8. Найдем характеристическую функцию случайной величины Z. Из свойства (7.14) характеристической функции имеем: (12.8) Подставив (12.5) и
- 9. Тогда Теорема. (12.10)
- 10. Пример 1. (12.11) Пример 2. (12.12)
- 12. Скачать презентацию








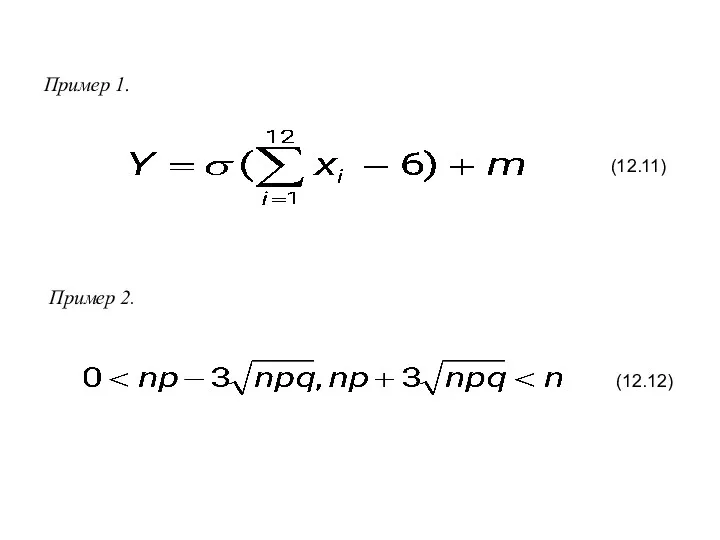
 Многомерная линейная регрессия
Многомерная линейная регрессия Урок математики по теме Свойства сложения, 2 класс
Урок математики по теме Свойства сложения, 2 класс Тройные интегралы
Тройные интегралы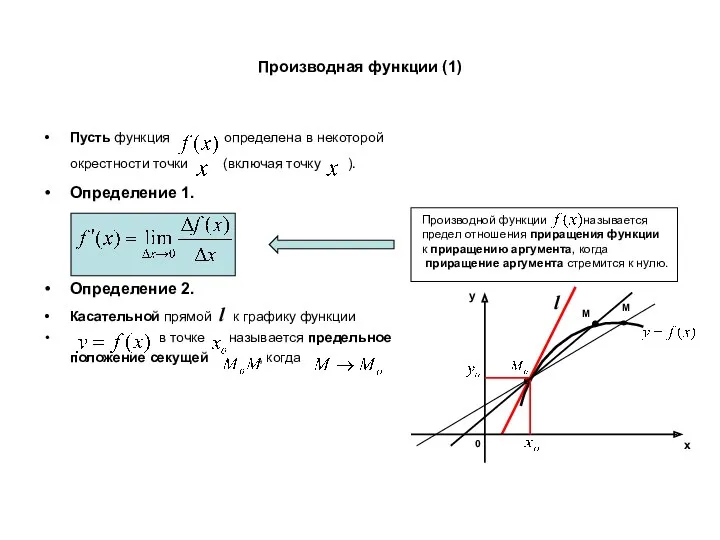 Производная функции
Производная функции Правило решения квадратных уравнений. Историческая справка
Правило решения квадратных уравнений. Историческая справка Отношения эквивалентности и порядка
Отношения эквивалентности и порядка Применение ленты Мёбиуса
Применение ленты Мёбиуса Проект по математике в 4 классе Мир в движении
Проект по математике в 4 классе Мир в движении Цилиндр. Определение цилиндра, развёртка цилиндра, формулы для вычисления
Цилиндр. Определение цилиндра, развёртка цилиндра, формулы для вычисления Давайте, посчитаем!
Давайте, посчитаем! Логикалық операциялар (дизъюнкция, конъюнкция, инверсия)
Логикалық операциялар (дизъюнкция, конъюнкция, инверсия) Методы оптимизации
Методы оптимизации Синус, косинус и тангенс острого угла прямоугольного треугольника
Синус, косинус и тангенс острого угла прямоугольного треугольника Электронный тренажёр по математике.
Электронный тренажёр по математике. Векторы. Сложение векторов
Векторы. Сложение векторов Умножение и деление обыкновенных дробей
Умножение и деление обыкновенных дробей проверка деления с остатком
проверка деления с остатком Параллельные прямые
Параллельные прямые Понятие формы. Многообразие форм окружающего мира
Понятие формы. Многообразие форм окружающего мира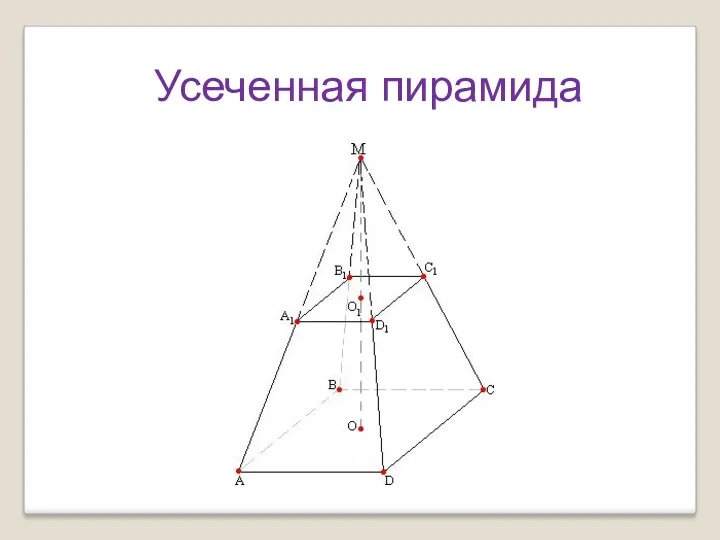 Усеченная пирамида
Усеченная пирамида Система линейных алгебраических уравнений (СЛАУ)
Система линейных алгебраических уравнений (СЛАУ) Деление дробей
Деление дробей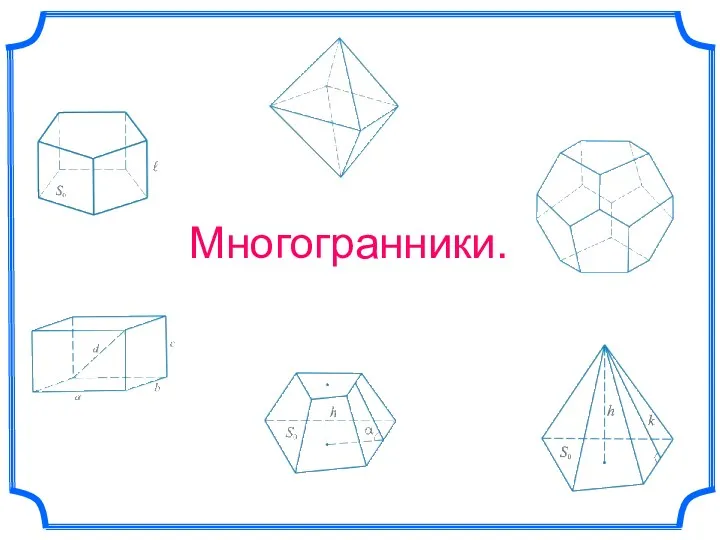 Многогранники. Выпуклые и невыпуклые многогранники
Многогранники. Выпуклые и невыпуклые многогранники Принципы симметрии
Принципы симметрии Теория вероятностей. Статистические методы обработки информации
Теория вероятностей. Статистические методы обработки информации Распознавание и называние геометрических тел: куб, шар, пирамида, цилиндр
Распознавание и называние геометрических тел: куб, шар, пирамида, цилиндр Решение уравнений. 6 класс
Решение уравнений. 6 класс Взаимное расположение графиков линейных функций
Взаимное расположение графиков линейных функций