Содержание
- 2. Алгоритм поиска оптимальных параметров бурения Построение математических моделей, отражающих влияние параметров на «отклики бурения» по методу
- 3. Факторный эксперимент считается полным, если в нем учтены все возможные комбинации на двух или трех уровнях.
- 4. осевая нагрузка – Рос; частота вращения – ω. В качестве факторов принимаются: Для проведения работы необходимо
- 5. X=A+B*Pоc +C* ω+D* Pос ω, где X- исследуемый параметр, A,B,C,D- коэффициенты уравнения, характеризующие степень влияния факторов
- 6. где z1,z2,z3,z4 – усредненные значения откликов, полученные экспериментально при проведении опытов Расчет коэффициентов
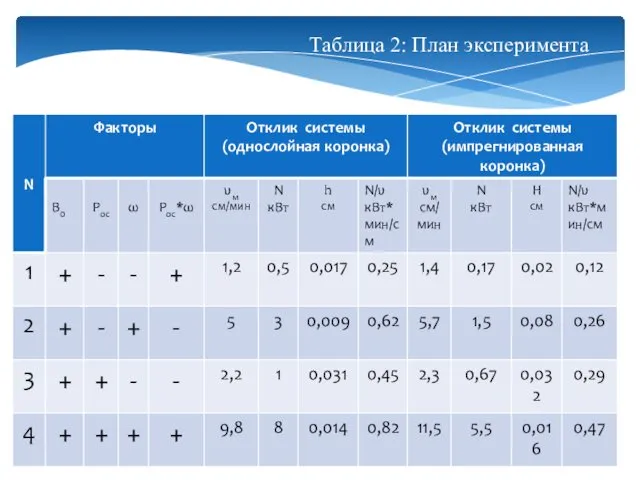
- 7. Таблица 2: План эксперимента
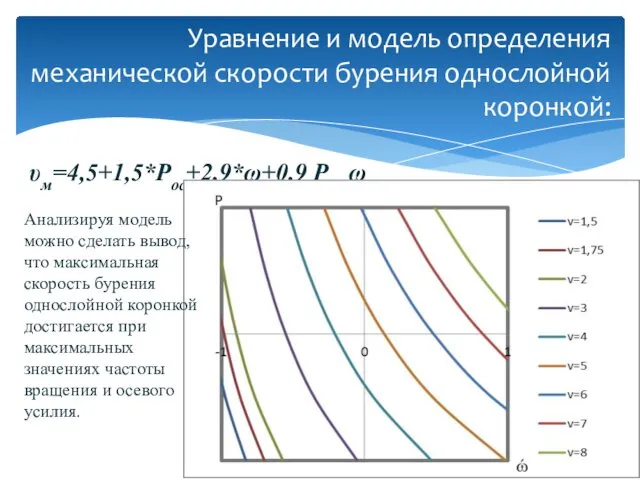
- 8. υм=4,5+1,5*Pос+2,9*ω+0,9 Pос ω Уравнение и модель определения механической скорости бурения однослойной коронкой: Анализируя модель можно сделать
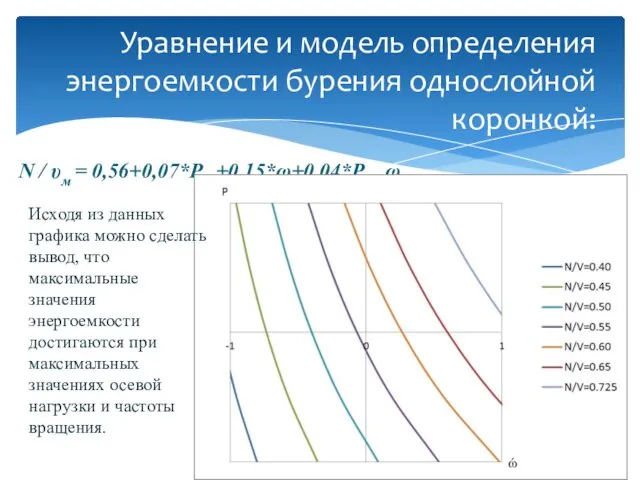
- 9. N / υм = 0,56+0,07*Pос+0,15*ω+0,04*Pос ω Уравнение и модель определения энергоемкости бурения однослойной коронкой: Исходя из
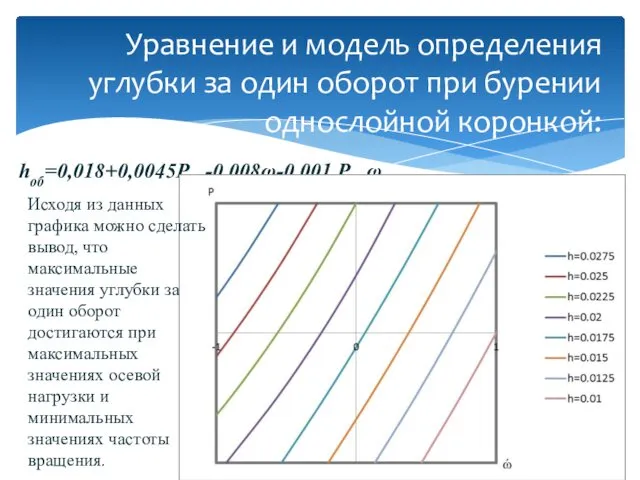
- 10. hоб=0,018+0,0045Pос -0,008ω-0,001 Pос ω Уравнение и модель определения углубки за один оборот при бурении однослойной коронкой:
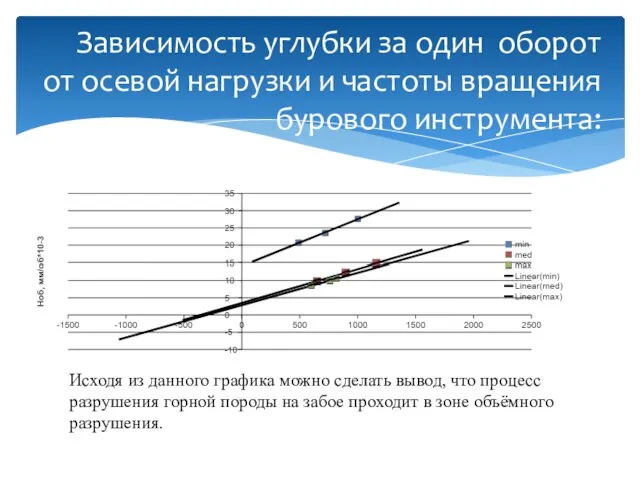
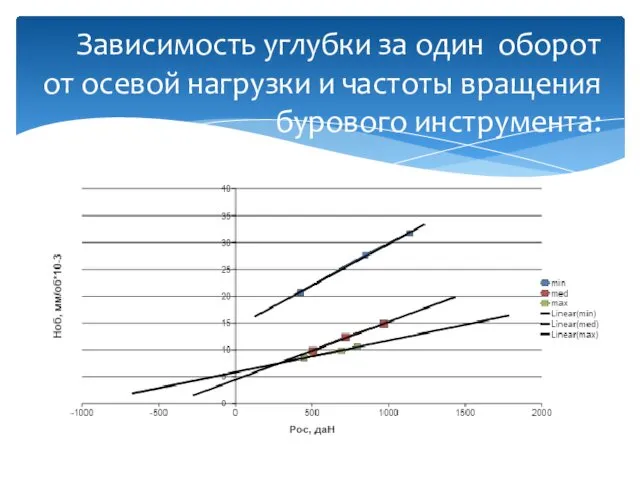
- 11. Зависимость углубки за один оборот от осевой нагрузки и частоты вращения бурового инструмента: Исходя из данного
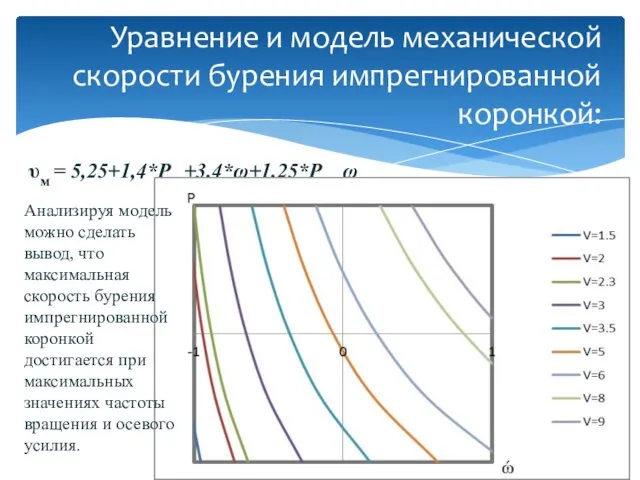
- 13. Уравнение и модель механической скорости бурения импрегнированной коронкой: υм = 5,25+1,4*Pос+3,4*ω+1,25*Pос ω Анализируя модель можно сделать
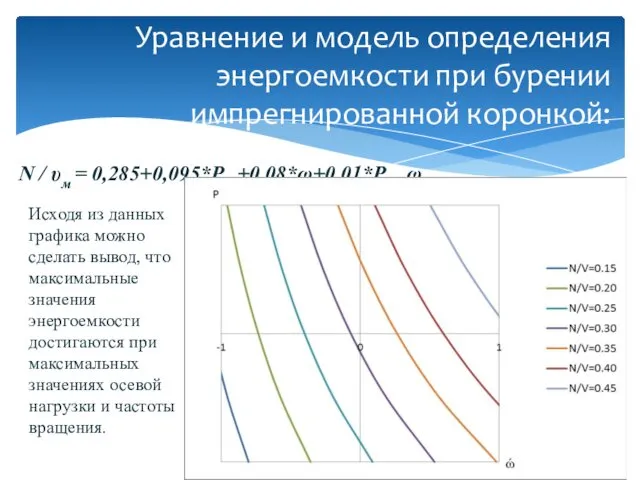
- 14. N / υм = 0,285+0,095*Pос+0,08*ω+0,01*Pос ω Уравнение и модель определения энергоемкости при бурении импрегнированной коронкой: Исходя
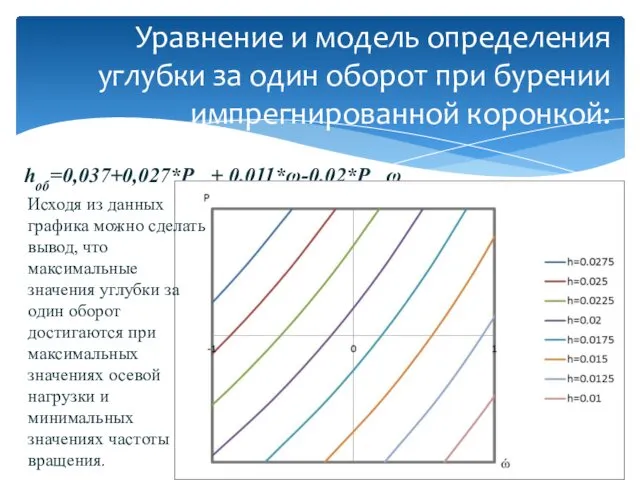
- 15. hоб=0,037+0,027*Pос + 0,011*ω-0,02*Pос ω Уравнение и модель определения углубки за один оборот при бурении импрегнированной коронкой:
- 16. Зависимость углубки за один оборот от осевой нагрузки и частоты вращения бурового инструмента:
- 18. Скачать презентацию






 Распространенные названия некоторых неорганических веществ
Распространенные названия некоторых неорганических веществ Под Андреевским флагом
Под Андреевским флагом Система каротажа при бурении. Занятие 9
Система каротажа при бурении. Занятие 9 Факторный анализ
Факторный анализ Регуляция клеточного цикла и биологическая роль митоза и мейоза
Регуляция клеточного цикла и биологическая роль митоза и мейоза физминутка для малышей Ножки и ладошки
физминутка для малышей Ножки и ладошки Первая медицинская помощь при травмах опорно-двигательного аппарата
Первая медицинская помощь при травмах опорно-двигательного аппарата Виртуальная реальность
Виртуальная реальность Бобовые. Мотыльковые
Бобовые. Мотыльковые Уголовная ответственность и состав преступления
Уголовная ответственность и состав преступления Увлекательная викторина для начальной школы В царстве растений.
Увлекательная викторина для начальной школы В царстве растений. Автоматизация звука Ш. Презентация Искатель.
Автоматизация звука Ш. Презентация Искатель. Akihoto Facades 3
Akihoto Facades 3 Пост. Великопостная молитва Св. Ефрема Сирина
Пост. Великопостная молитва Св. Ефрема Сирина Церкви Новосибирской области. Диск
Церкви Новосибирской области. Диск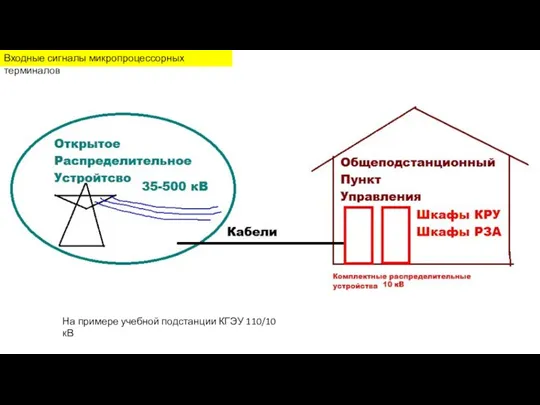 Входные сигналы микропроцессорных терминалов
Входные сигналы микропроцессорных терминалов Геометрия для малышей Итоговое занятия Уроки тетушки совы
Геометрия для малышей Итоговое занятия Уроки тетушки совы Базовые принципы Фон Неймана
Базовые принципы Фон Неймана Покажи свое настроение. Задача для лисенка
Покажи свое настроение. Задача для лисенка Полупроводниковые материалы и их свойства
Полупроводниковые материалы и их свойства Туберкулез. Первичное инфицирование
Туберкулез. Первичное инфицирование Общая психиатрия. Организация психиатрической помощи в РФ
Общая психиатрия. Организация психиатрической помощи в РФ Микропроцессорные системы
Микропроцессорные системы Мученичество. Часть 2
Мученичество. Часть 2 Расчёт показателей непоршневого вытеснения нефти водой с оценкой возможности их регулирования изменением
Расчёт показателей непоршневого вытеснения нефти водой с оценкой возможности их регулирования изменением Лабораторная работа №7 Тема: Устройство нивелиров
Лабораторная работа №7 Тема: Устройство нивелиров Тренажёр Работаем над техникой чтения
Тренажёр Работаем над техникой чтения Европейский Север
Европейский Север