Содержание
- 2. Численное дифференцирование и интегрирование функций 5.1. Постановка вопроса Найти производные указанных порядков от функции f(x), заданной
- 3. 5.2. Приближенное дифференцирование на основе первой интерполяционной формулы Ньютона Пусть функция y(x) задана в равноотстоящих точках
- 4. Перемножая биномы получим Учтем Далее, поскольку В результате: получим Аналогично можно получить формулы и для производных
- 5. 5.3. Приближенное дифференцирование для равноотстоящих точек (узлов), выраженных через значения функций в этих точках на основе
- 6. Полагая получим Тогда, для полинома Лагранжа имеем Учитывая то, что Получаем
- 7. Погрешность вычисления первой производной: Для Rn получим Тогда, Если число узлов нечетно и производная берется в
- 8. 5.4. Приближенное интегрирование функций. Общие замечания Если функция f(x) непрерывна на отрезке [a,b] и известна ее
- 9. Пусть функция y = f(x) задана на отрезке [a,b]. С помощью точек x0, x1…, xn разобьем
- 10. 5.7. Метод трапеций В этом методе используется линейная интерполяция функции y=f(x) в промежутках между узлами. (i=1,
- 11. 5.8. Уточненные значения интегралов Погрешность численного метода в общем случае равна Главный член погрешности интеграла (I1),
- 12. 5.9. Метод парабол (метод Симпсона) Разобьем отрезок интегрирования [a,b] на четное число n равных частей с
- 13. Просуммировав все отрезки, получим: Значение S принимается в качестве определенного интеграла. Окончательное выражение для формулы Симпсона
- 14. 5.10. Формула Ньютона-Кортеса Пусть для данной функции y=f(x) необходимо вычислить определенный интеграл. где Ai – некоторые
- 15. где постоянные коэффициента Hi называются коэффициентами Кортеса : Окончательный вид квадратурной формулы Ньютона-Кортеса: где Коэффициенты Кортеса
- 16. Остаточный член формулы Ньютона-Котеса: где E(n/2) – целая часть дроби n/2. Таким образом, нечетное число ординат
- 17. 5.11. Квадратурная формула Гаусса Полиномы Лежандра Важные свойства полиномов: где Qk –любой полином степени k Полином
- 18. Рассмотрим функцию f(t), заданную на отрезке [-1, 1]. при k четном, Учитывая соотношение при k нечетном
- 19. Так как степени этих полиномов не превышают 2n-1, то на основании системы (2) для них должна
- 20. Подстановка в эту формулу f(t) дает : В силу ортогональности полиномов Лежандра или Это равенство будет
- 21. 5.12. Дифференцирование и интегрирование в пакете MathCad
- 22. 6. Численное решение дифференциальных уравнений 6.1. Основные понятия Дифференциальные уравнения делятся на: обыкновенные (содержащие одну переменную),
- 23. Линейными дифференциальными уравнениями называются уравнения, линейные относительно искомой функции и её производных. Решением дифференциального уравнения всякая
- 24. Для выделения некоторого частного решения линейного дифференциального уравнения первого порядка достаточно задать координаты некоторой точки (x0,y0)
- 25. 6.2.1. Метод Эйлера Решить дифференциальное уравнение dy/dx=f(x,y) численным методом , значит для заданной последовательности аргументов x0,
- 26. 6.2.1. Метод Рунге-Кутта Этот метод является методом повышенной точности. Как и в методе Эйлера yi= yi-1+Δyi-1,
- 27. 6.2.2. Метод Рунге-Кутта в пакете MathCad
- 28. 6.3. Приближенные методы решения краевой задачи для линейного обыкновенного дифференциального уравнения Рассмотрим уравнение вида Краевая задача
- 29. 6.4.1. Метод коллокаций В этом методе выбираются n точек xi, принадлежащих отрезку [a,b], называемых точками коллокации
- 30. 6.4.4. Метод стрельбы Рассмотрим краевую задачу для уравнения второго порядка, разрешенного относительно второй производной. Сущность метода
- 32. Скачать презентацию







![Пусть функция y = f(x) задана на отрезке [a,b]. С](/_ipx/f_webp&q_80&fit_contain&s_1440x1080/imagesDir/jpg/63339/slide-8.jpg)


![5.9. Метод парабол (метод Симпсона) Разобьем отрезок интегрирования [a,b] на](/_ipx/f_webp&q_80&fit_contain&s_1440x1080/imagesDir/jpg/63339/slide-11.jpg)





![Рассмотрим функцию f(t), заданную на отрезке [-1, 1]. при k](/_ipx/f_webp&q_80&fit_contain&s_1440x1080/imagesDir/jpg/63339/slide-17.jpg)












 Украшение предметов домашней утвари в технике декупаж
Украшение предметов домашней утвари в технике декупаж Теории происхождения жизни на Земле
Теории происхождения жизни на Земле Реконструкция технологического процесса погрузочно-разгрузочных работ с комплексной переработкой пиловочного сырья
Реконструкция технологического процесса погрузочно-разгрузочных работ с комплексной переработкой пиловочного сырья Способы поверхностного упрочнения
Способы поверхностного упрочнения Альтернативные источники энергии
Альтернативные источники энергии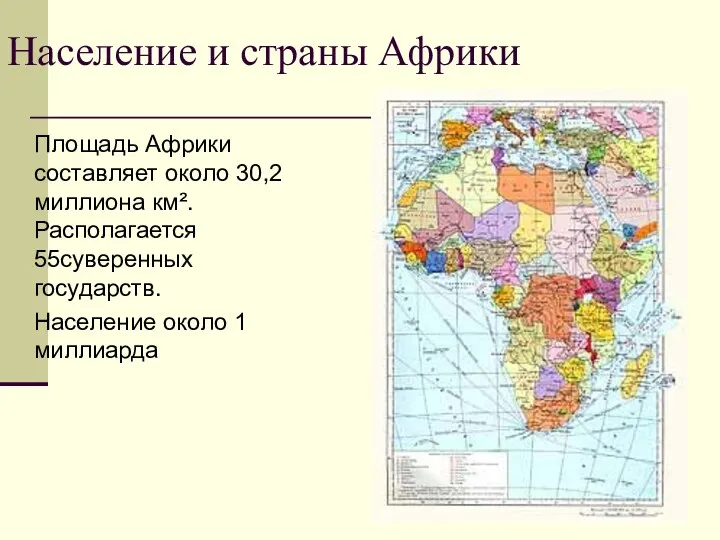 7 класс: Население и государства Африки
7 класс: Население и государства Африки Словo Жыцця. Красавiк 2016. “Тое, што вы зрабілі аднаму з гэтых братоў Маіх меншых, вы Мне зрабілі” (Мц 25,40)
Словo Жыцця. Красавiк 2016. “Тое, што вы зрабілі аднаму з гэтых братоў Маіх меншых, вы Мне зрабілі” (Мц 25,40) Радуга, федеральная аптечная сеть
Радуга, федеральная аптечная сеть Хәсән Туфан
Хәсән Туфан Дифференциация звуков К - Г
Дифференциация звуков К - Г Происхождение жизни на Земле
Происхождение жизни на Земле Казахская кухня
Казахская кухня Функции таможенных органов согласно таможенному кодексу РФ
Функции таможенных органов согласно таможенному кодексу РФ Кіномистецтво
Кіномистецтво Создание условий для двигательной активности в детском саду. Консультация для воспитателей.
Создание условий для двигательной активности в детском саду. Консультация для воспитателей. 20181013_rasteniya_ao
20181013_rasteniya_ao Полезные и вредные привычки
Полезные и вредные привычки Презентация Мои любимые сказки
Презентация Мои любимые сказки Социально значимый проект Мой любимый уголок станицы
Социально значимый проект Мой любимый уголок станицы Технология асинхронного режима передачи. (Лекция 6)
Технология асинхронного режима передачи. (Лекция 6) Классный уголок
Классный уголок Теплоснабжение многоквартирных домов
Теплоснабжение многоквартирных домов Мягкая игрушка. Мишка
Мягкая игрушка. Мишка Вырубка лесов в Нижегородской области
Вырубка лесов в Нижегородской области Пелагіаль (лекція 4)
Пелагіаль (лекція 4) Сталинград-город герой
Сталинград-город герой Классификация электрических машин
Классификация электрических машин Japan_Country rules_Babich A_PZ-2004
Japan_Country rules_Babich A_PZ-2004