Содержание
- 2. Декартовы прямоугольные координаты на плоскости и в пространстве. Система координат Определение 1. Прямая, служащая для изображения
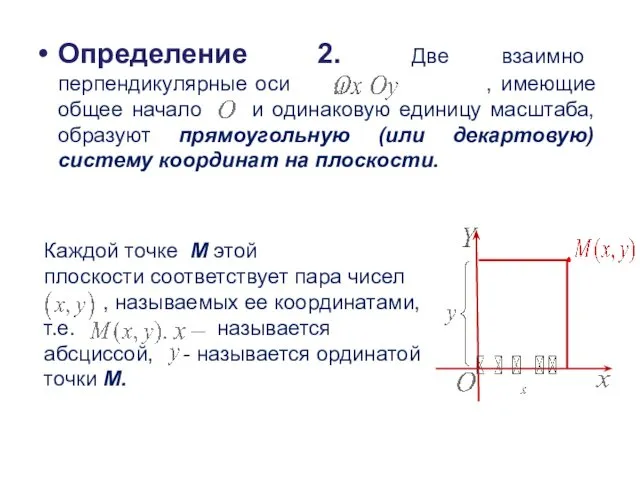
- 3. Определение 2. Две взаимно перпендикулярные оси , имеющие общее начало и одинаковую единицу масштаба, образуют прямоугольную
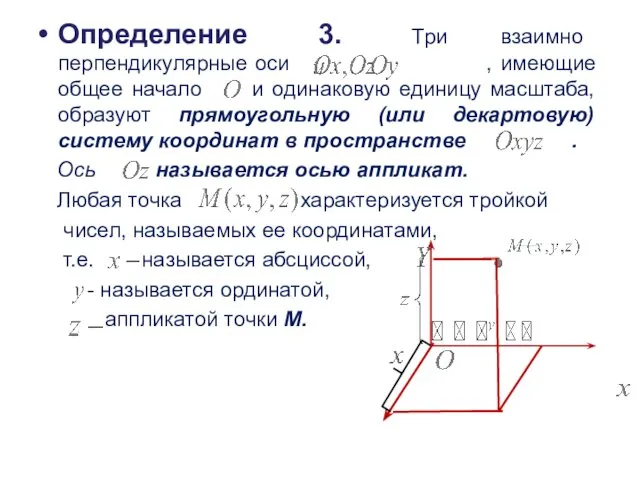
- 4. Определение 3. Три взаимно перпендикулярные оси , имеющие общее начало и одинаковую единицу масштаба, образуют прямоугольную
- 5. О П Р Е Д Е Л Е Н И Я 1. Вектором называется направленный отрезок
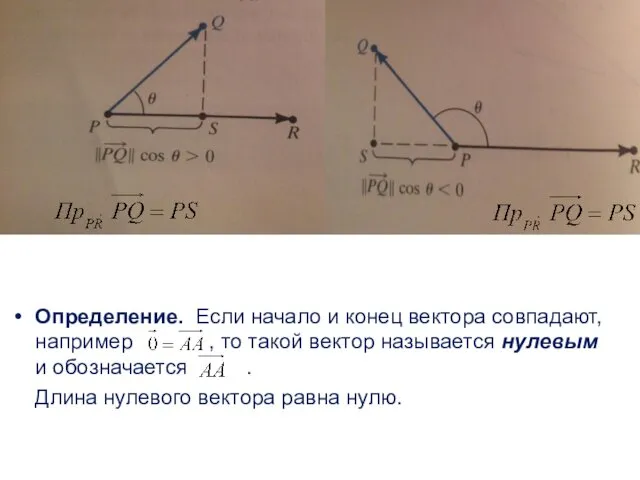
- 6. Определение. Если начало и конец вектора совпадают, например , то такой вектор называется нулевым и обозначается
- 7. 5. Направляющими углами вектора называются углы между ним и координатными осями: 6. Косинусы направляющих углов называются
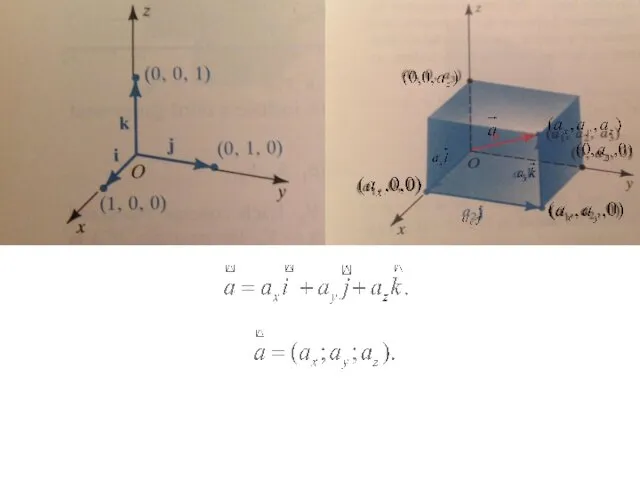
- 9. Вектор также обозначается З а м е ч а н и е 2. Для любого вектора
- 10. З а м е ч а н и е 5. Длина вектора через координаты определяется по
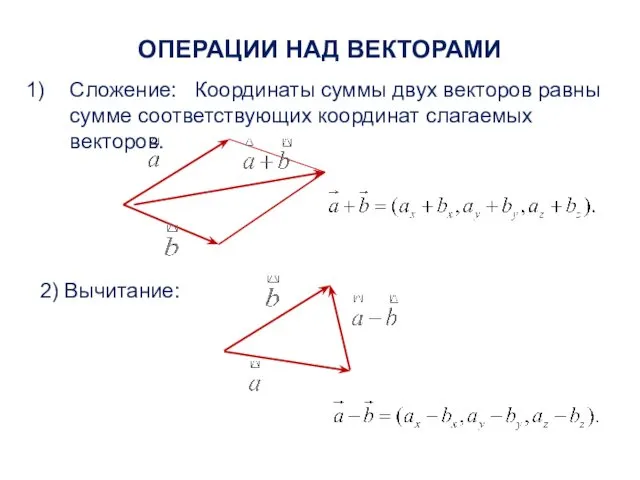
- 11. ОПЕРАЦИИ НАД ВЕКТОРАМИ Сложение: Координаты суммы двух векторов равны сумме соответствующих координат слагаемых векторов. 2) Вычитание:
- 12. 3) Умножение вектора на скаляр 4) Скалярное произведение двух векторов. О п р е д е
- 13. Свойства скалярного произведения 1. 2. 3. 4. 5. угол между двумя векторами
- 14. Пример Даны векторы : Найти:
- 15. Решение. По определению Найдем длины векторов и . По формуле найдем Скалярный квадрат равен квадрату модуля
- 17. Скачать презентацию









 Охота на сома методом квока
Охота на сома методом квока 20190502_kompleksnyy_podhod_k_organizatsii_logopedicheskih_korrektsionno-razvivayushchih_zanyatiy
20190502_kompleksnyy_podhod_k_organizatsii_logopedicheskih_korrektsionno-razvivayushchih_zanyatiy Основные системы налогообложения, порядок их применения
Основные системы налогообложения, порядок их применения Канада. Характеристика региона
Канада. Характеристика региона Синтоизм
Синтоизм Экология и здоровье человека
Экология и здоровье человека Дид игра С какого дерева листок
Дид игра С какого дерева листок Линейные уравнения
Линейные уравнения Высокоточные системы навигации. Лекция №1.2
Высокоточные системы навигации. Лекция №1.2 Первое знакомство с задачами - для родителей
Первое знакомство с задачами - для родителей Антарктида.
Антарктида. Презентация Круг
Презентация Круг Пневматические сеялки Salford
Пневматические сеялки Salford Мифы выбора профессии
Мифы выбора профессии Частотные преобразователи
Частотные преобразователи Школа-студия киномастерства Марсы
Школа-студия киномастерства Марсы Лидеры. Девиз один - не уступать. Стартуем, чтобы побеждать
Лидеры. Девиз один - не уступать. Стартуем, чтобы побеждать Классный час. 4 Б класс.Итоги 1 четверти.2012 -2013 уч.год.
Классный час. 4 Б класс.Итоги 1 четверти.2012 -2013 уч.год. Урок развития речи в 6 классе
Урок развития речи в 6 классе Information Systems
Information Systems Скребковые конвейеры
Скребковые конвейеры Фонтанная эксплуатация скважин
Фонтанная эксплуатация скважин Приложение 1 к уроку по теме Озёра. Презентация. часть 3
Приложение 1 к уроку по теме Озёра. Презентация. часть 3 Дошкольное образование. Музейная педагогика. Мини-музей Югра.
Дошкольное образование. Музейная педагогика. Мини-музей Югра. Компоненты электроники
Компоненты электроники Логопедическое занятие Дифференциация звуков с-з в слогах и словах
Логопедическое занятие Дифференциация звуков с-з в слогах и словах Гипотоническая болезнь. Коллапс
Гипотоническая болезнь. Коллапс Көкірек ортаның және өкпенің іріңді аурулары
Көкірек ортаның және өкпенің іріңді аурулары