Содержание
- 2. 5. ДИФФЕРЕНЦИРОВАНИЕ ФУНКЦИИ ОДНОГО АРГУМЕНТА 5.1 Определение производной 5.2 Геометрический смысл производной 5.3 Связь между непрерывностью
- 3. 5.1 ОПРЕДЕЛЕНИЕ ПРОИЗВОДНОЙ Пусть функция y = f(x) определена в некотором интервале (a; b). Аргументу x
- 4. 5.1 ОПРЕДЕЛЕНИЕ ПРОИЗВОДНОЙ Итак, по определению: Функция y = f(x) , имеющая производную в каждой точке
- 5. 5.2 ГЕОМЕТРИЧЕСКИЙ СМЫСЛ ПРОИЗВОДНОЙ Возьмем на непрерывной кривой L две точки М и М1: х f(x
- 6. 5.2 ГЕОМЕТРИЧЕСКИЙ СМЫСЛ ПРОИЗВОДНОЙ Производная f ′(x) равна угловому коэффициенту касательной к графику функции y =
- 7. 5.3 СВЯЗЬ МЕЖДУ НЕПРЕРЫВНОСТЬЮ И ДИФФЕРЕНЦИРУЕМОСТЬЮ ФУНКЦИИ Если функция y = f(x) дифференцируема в некоторой точке,
- 8. 5.4 ПРОИЗВОДНЫЕ ОСНОВНЫХ ЭЛЕМЕНТАРНЫХ ФУНКЦИЙ Таблица производных (без вывода)
- 9. 5.4 ПРОИЗВОДНЫЕ ОСНОВНЫХ ЭЛЕМЕНТАРНЫХ ФУНКЦИЙ Таблица производных (без вывода)
- 10. 5.5 ПРАВИЛА ДИФФЕРЕНЦИРОВАНИЯ Пусть u(x) , v(x) и w(x) – дифференцируемые в некотором интервале (a; b)
- 11. 5.6 ПРОИЗВОДНАЯ СЛОЖНОЙ ФУНКЦИИ Пусть даны функции y = f(u) и u = φ(x) , тогда
- 12. 5.6 ПРОИЗВОДНАЯ СЛОЖНОЙ ФУНКЦИИ Вычислить производную функции
- 13. 5.7 ПРОИЗВОДНАЯ ОБРАТНОЙ ФУНКЦИИ Пусть задана дифференцируемая функция y = f(x) и f ′(x) ≠ 0
- 14. 5.8 ПРОИЗВОДНАЯ НЕЯВНО ЗАДАННОЙ ФУНКЦИИ Если функция задана уравнением y = f(х) , разрешенным относительно y,
- 15. 5.9 ЛОГАРИФМИЧЕСКОЕ ДИФФЕРЕНЦИРОВАНИЕ Такую операцию называют логарифмическим дифференцированием. В ряде случаев для нахождения производной целесообразно заданную
- 16. 5.9 ЛОГАРИФМИЧЕСКОЕ ДИФФЕРЕНЦИРОВАНИЕ Для применения логарифмического дифференцирования необходимо вспомнить свойства логарифмов: Найти производные следующих функций:
- 17. 5.10 ПРОИЗВОДНАЯ ФУНКЦИИ, ЗАДАННОЙ ПАРАМЕТРИЧЕСКИ Выведем формулу для нахождения производной этой функции: Пусть функция y =
- 18. 5.10 ПРОИЗВОДНАЯ ФУНКЦИИ, ЗАДАННОЙ ПАРАМЕТРИЧЕСКИ Вычислить производные следующих функций, заданных параметрически:
- 20. Скачать презентацию

















 Предельные углеводороды. Химические свойства. 10 класс
Предельные углеводороды. Химические свойства. 10 класс Создание 3D модели видеокарты NVIDIA GEFORCE GTS 450. Устройство и принцип её работы
Создание 3D модели видеокарты NVIDIA GEFORCE GTS 450. Устройство и принцип её работы Гофрированный картон
Гофрированный картон Засади конституційного ладу
Засади конституційного ладу Первая группа раннего возраста
Первая группа раннего возраста Ребусы
Ребусы Культура древнего Китая
Культура древнего Китая Экологиялық аймақта тұратын науқастарда аллергиялық ринит кезінде антигистаминді препарат (лоратадин) тиімділігін бағалау
Экологиялық аймақта тұратын науқастарда аллергиялық ринит кезінде антигистаминді препарат (лоратадин) тиімділігін бағалау Виды сварных соединений и швов
Виды сварных соединений и швов Притча о трещине в кувшине
Притча о трещине в кувшине Презентация Какие растения самые важные
Презентация Какие растения самые важные Государственная тайна
Государственная тайна Концепция развития автомобильной отрасли в России
Концепция развития автомобильной отрасли в России Компетентностный подход в работе с персоналом. Компетенции работников образовательного учреждения и бизнес-компетенции
Компетентностный подход в работе с персоналом. Компетенции работников образовательного учреждения и бизнес-компетенции И. Токмакова Мы играли в хохотушки, Я. Тайц Волк, Г. Кружков РРРы!
И. Токмакова Мы играли в хохотушки, Я. Тайц Волк, Г. Кружков РРРы! Ознакомление детей дошкольного возраста с декоративно-прикладным искусством
Ознакомление детей дошкольного возраста с декоративно-прикладным искусством Определение основных параметров криволинейного остряка
Определение основных параметров криволинейного остряка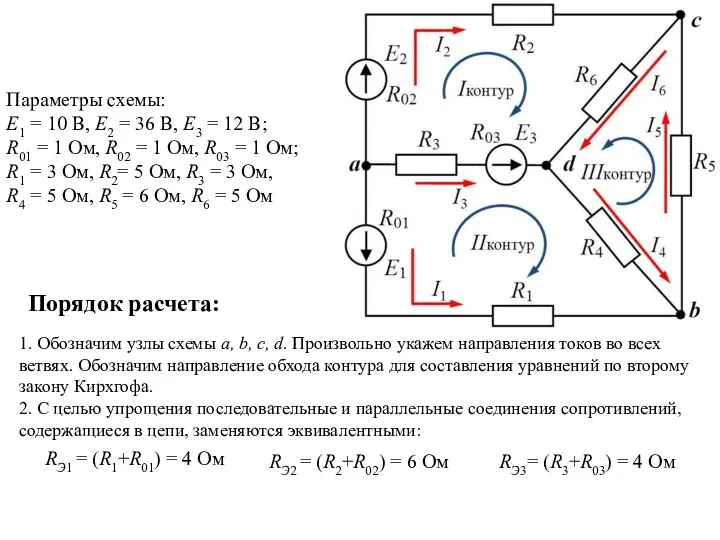 Расчет цепи постоянного тока
Расчет цепи постоянного тока Семья как субьект педагогического взаимодействия
Семья как субьект педагогического взаимодействия Бюджет государства и семьи
Бюджет государства и семьи Совершенствование размольного отделения Ново-Альжанского мукомольного завода в г. Актобе с увеличением производительности
Совершенствование размольного отделения Ново-Альжанского мукомольного завода в г. Актобе с увеличением производительности Презентация Бабочки из пластиковых бутылок.
Презентация Бабочки из пластиковых бутылок. Технология изготовления балки для эстакад
Технология изготовления балки для эстакад Химический состав клетки
Химический состав клетки Chinese Cuisine
Chinese Cuisine Одноелектронні прилади та пристрої
Одноелектронні прилади та пристрої Кислотные дожди
Кислотные дожди Портфолио для начальных классов Ну погоди
Портфолио для начальных классов Ну погоди