Элементы математической логики презентация

Историческая справка:
Математическая логика – раздел математики, изучающий математические доказательства и вопросы оснований математики.
Логика как наука сформировалась в 4 в. до н.э. Ее создал греческий ученый Аристотель.
Слово «логика» происходит от греческого "логос", что с одной стороны означает "слово" или "изложение", а с другой мышление.

В 17 в. немецкий ученый Лейбниц задумал создать новую науку, которая была бы «искусством исчисления истины». В этой логике, по мысли Лейбница, каждому высказыванию соответствовал бы символ, а рассуждения имели бы вид вычислений.
Эта идея Лейбница, не встретив понимания современников, не получила распространения и развития.

Только в середине 19 в. ирландский математик Джордж Буль воплотил идею Лейбница. В 1854 году им была написана работа "Исследование законов мышления", которая заложила основы алгебры логики, в которой действуют законы, схожие с законами обычной алгебры, но буквами обозначаются не числа, а высказывания.

На языке булевой алгебры можно описать рассуждения и "вычислить" их результаты. Однако ею охватываются далеко не все рассуждения, а лишь определенный тип их, поэтому алгебру Буля считают исчислением высказываний.

АЛГЕБРА ВЫСКАЗЫВАНИЙ
Основными понятиями логики высказываний являются высказывания и логические связки (операции над высказываниями).
В логике предикатов используются еще предикаты и кванторы.

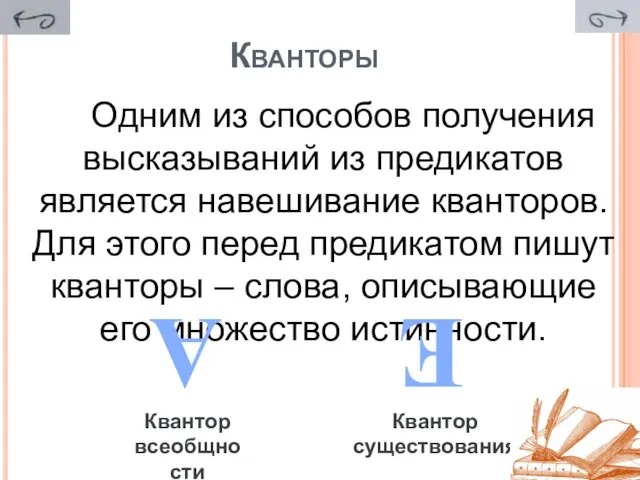
Кванторы
Одним из способов получения высказываний из предикатов является навешивание кванторов. Для этого перед предикатом пишут кванторы – слова, описывающие его множество истинности.
А
Е
Квантор
существования
Квантор всеобщности

квантор существования « ∃»
Квантор существования — это символ, обозначающий единственное существование и читается как «существует» или «для некоторого».
Из предиката {Ученик X Лицея города Тюмени сдал ЕГЭ по математике более чем на 70 баллов } получаются высказывание:
{Найдется такой ученик Лицея города Тюмени, который сдаст ЕГЭ по математике более чем на 70 баллов}

квантор всеобщности «∀»
Квантор всеобщности — это символ, обозначающий всеобщность и читается как «для любого» или «для всех».
Из предиката {Ученик X Лицея сдал ЕГЭ по математике более чем на 70 баллов } получаются высказывание:
{Все ученики Лицея сдали ЕГЭ по математике более чем на 70 баллов}

Высказывания и не только в нашей жизни…

МЫШЛЕНИЕ осуществляется через:
Понятия
Высказывания
Умозаключения

ВЫСКАЗЫВАНИЕ
формулировка своего понимания окружающего мира (повествовательное предложение в котором что-либо утверждается или отрицается)
(Пример: Париж – столица Франции)

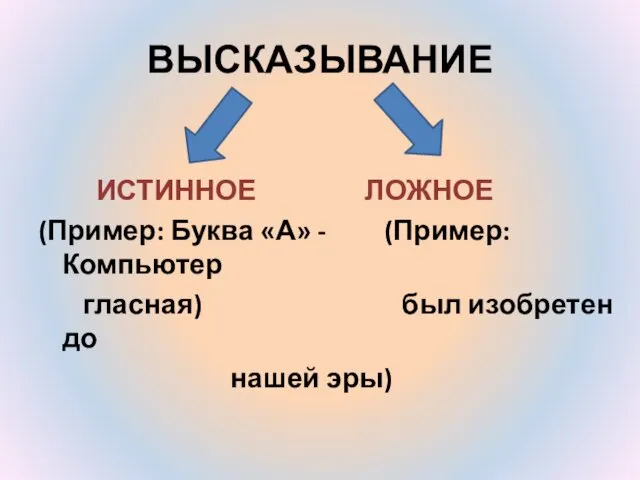
ВЫСКАЗЫВАНИЕ
ИСТИННОЕ ЛОЖНОЕ
(Пример: Буква «А» - (Пример: Компьютер
гласная) был изобретен до
нашей эры)

УМОЗАКЛЮЧЕНИЕ
форма мышления, с помощью которой из одного или нескольких суждений может быть получено новое суждение
(знание или вывод)
(Пример: любая теорема)

Вопросительные, повелительные и бессмысленные предложения не являются логическими высказываниями.
По аналогии с элементарной алгеброй, где любое число является константой, высказывание является логической константой, величина которой равна 1 или 0.

Пример:
предложение « 2x = 4» не является высказыванием. Для того чтобы имело смысл говорить об его истинности или ложности, необходимы некоторые дополнительные сведения. Конечно, достаточно знать, какое именно число обозначено буквой x.
Каждому значению переменной x будет соответствовать либо истинное, либо ложное высказывание; например, при х=2 высказывание истинно, при остальных ложно.

Операции над высказываниями
В логике над высказываниями производятся следующие основные операции (логические связки): отрицание, конъюнкция, дизъюнкция, импликация, эквиваленция, неравнозначность. Они рассматриваются как средство вычисления логического значения сложного высказывания по логическим значениям составляющих его простых высказываний.

Отрицание (логическая связка «не»)
Отрицанием (инверсией) высказывания A называется высказывание, которое истинно, если высказывание A ложно, и ложно, когда A истинно.
Отрицание является логической операцией, выполняемой над одним аргументом.
Таблица истинности:

Логическое умножение (конъюнкция)
Конъюнкция двух высказываний A и B — это сложное логическое высказывание, которое истинно только в случае истинности всех составляющих высказываний, в противном случае оно ложно. Обозначения: A & B, A ∧ B . Читается: « A и B».

Логическое сложение (дизъюнкция)
Дизъюнкция двух высказываний A и B — это сложное логическое высказывание, которое ложно только в случае ложности всех составляющих высказываний, в противном случае оно истинно.
Высказывание считается истинным, когда истинно хотя бы одно из составляющих высказываний.
Обозначается: A ∨ B , A + B. Читается: « A или B».

Логическое следование (импликация)
В математических доказательствах часто пользуются сложными высказываниями, образованными с помощью слов «если…, то…». Здесь высказывание, расположенное после слова «если», называется основанием (посылкой), а высказывание, расположенное после слова «то», называется следствием или заключением.
Импликацией двух высказываний A и B называется высказывание, обозначаемое символом A →B (A ⊃ B), которое ложно тогда и только тогда, когда A истинно, а B ложно.
Читается: «если A, то B» (« A влечет B», «из A следует B»).

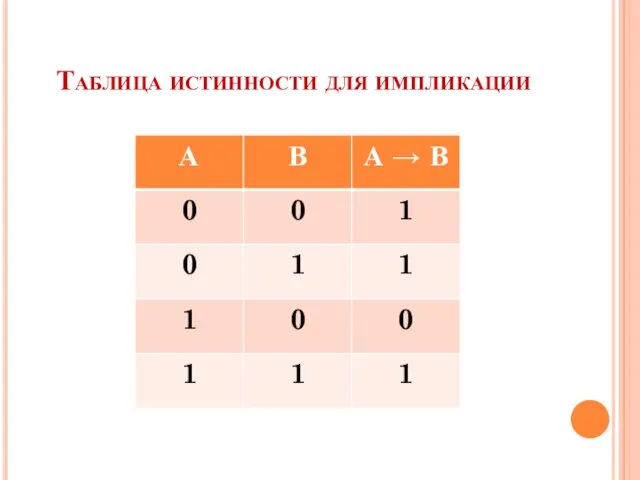
Таблица истинности для импликации

Пример:
Определение импликации вынуждает считать истинными такие предложения, как:
«Если 2×2=4, то Москва столица России».
Это связано с тем, что определениями логических операций смысл составляющих высказываний не учитывается, они рассматриваются как объекты, обладающие единственным свойством — быть истинными, либо ложными.

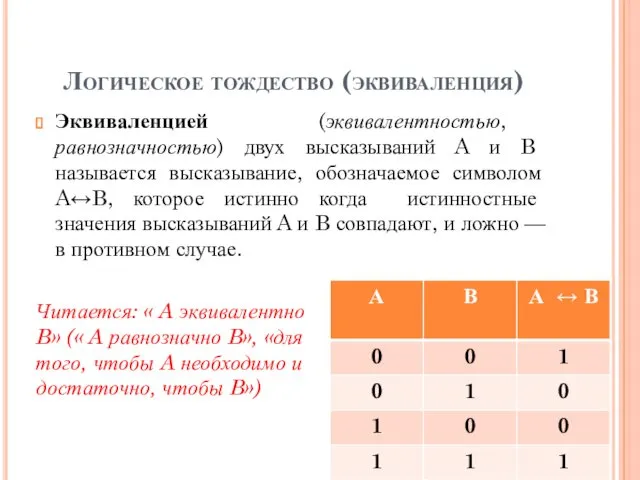
Логическое тождество (эквиваленция)
Эквиваленцией (эквивалентностью, равнозначностью) двух высказываний A и B называется высказывание, обозначаемое символом A↔B, которое истинно когда истинностные значения высказываний A и B совпадают, и ложно — в противном случае.
Читается: « A эквивалентно B» (« A равнозначно B», «для того, чтобы A необходимо и достаточно, чтобы B»)

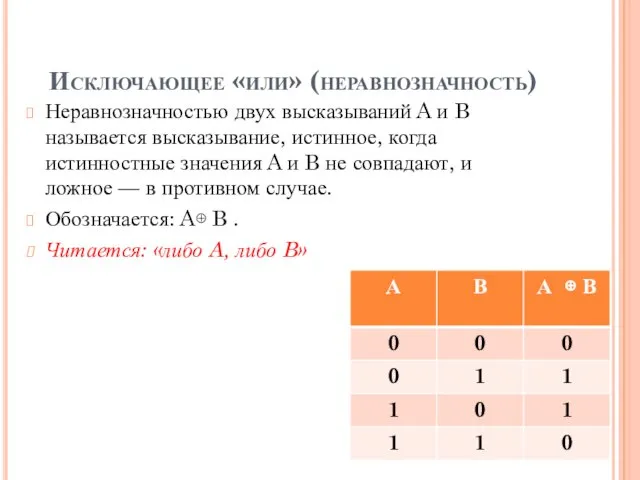
Исключающее «или» (неравнозначность)
Неравнозначностью двух высказываний A и B называется высказывание, истинное, когда истинностные значения A и B не совпадают, и ложное — в противном случае.
Обозначается: A⊕ B .
Читается: «либо A, либо B»

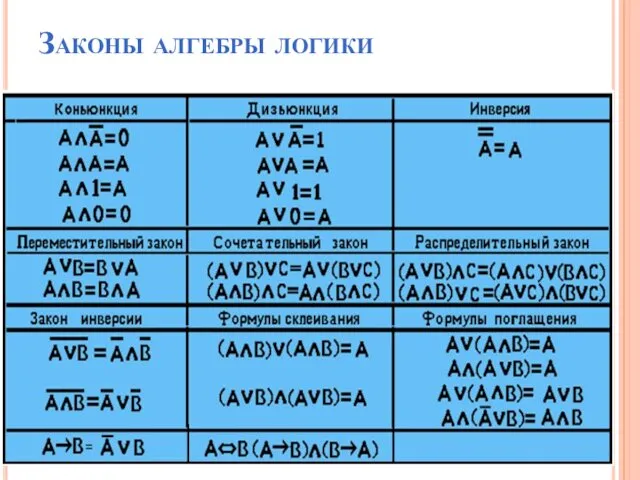
Законы алгебры логики

Для предикатов характерны те же действия, что и для высказываний, а именно: Конъюнкция
Дизъюнкция
Импликация
Эквиваленция и др.
ПРЕДИКАТЫ

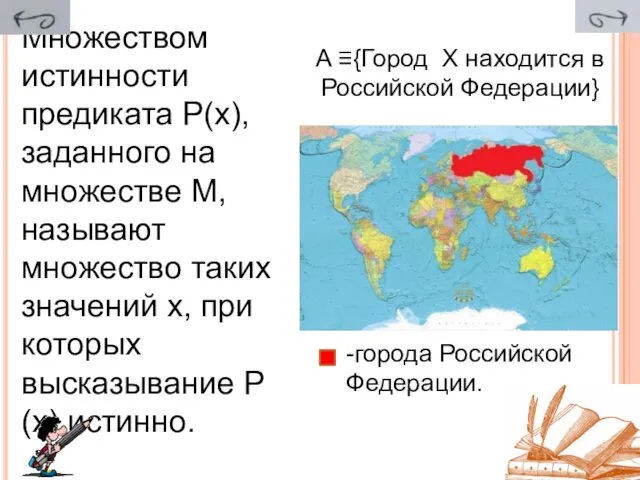
Множеством истинности предиката Р(х), заданного на множестве М, называют множество таких значений х, при которых высказывание Р(х) истинно.
-города Российской Федерации.
A ≡{Город Х находится в Российской Федерации}

Решение задач

Задача №1
Для какого числа X истинно высказывание:
((x<4)→(x<3))^((x<3)→(x<1))
1)1 2)2 3)3 4)4
Решение:
Подставляем в выражение предложенные варианты ответа и определяем, истинно выражение или ложно:
1) x=1: ((1<4)→(1<3))^((1<3)→(1<1))=(1→1)^(1→0)
Сначала вычислим выражение в скобках:
(1→1)^(1→0)=1^0=0 (не подходит)
Аналогично подставляем другие варианты ответа, вычисляем:
2) x=2: ((2<4)→(2<3))^((2<3)→(2<1))=(1→1)^(1→0)=1^0=0 (не подходит)
3) x=3: ((3<4)→(3<3))^((3<3)→(3<1))=(1→0)^(0→0)=0^1=0 (не подходит)
4) x=4: ((4<4)→(4<3))^((4<3)→(4<1))=(0→0)^(0→0)=1^1=1 (подходит)
Ответ: 4.
задания

Задача №2
Для какого имени ложно высказывание:
(первая буква гласная ^последняя буква согласная)→ ¬(третья буква согласная)?
Дмитрий 2) Антон 3) Екатерина 4) Анатолий
Решение:
Подставляем в выражение предложенные варианты ответа и определяем, истинно выражение или ложно:
Дмитрий: (0 ^ 1)→ ¬(0)=0→1 = 1 (не подходит)
Антон: (1 ^ 1)→ ¬(1)=1→0 = 0 (подходит)
Екатерина: (1 ^ 0)→ ¬(0)=0→1 = 1 ( не подходит)
Анатолий: (1 ^ 1)→ ¬(0)=1→1 = 1 ( не подходит)
Ответ: 2.
задания

Задача №3
Построить таблицу истинности для следующей функции:
F(X,Y,Z)=(x→y)·z + ¬y
Решение:
1) Нарисуем таблицу на K строк, где K=2n, n - количество
высказываний в функции
N=3, k=8 строк
2) Запишем в таблице все варианты X,Y,Z и вычисляем выражение по
действиям:
задания

Задача №4
Каково наименьшее натуральное число X, при котором
истинно высказывание
Решение: Импликация ложна, когда первое выражение истинно, а второе ложно(см. таблицы истинности). Во всех остальных случаях импликация истинна. Первое выражение ложно для всех натуральных x>10 и истинно для всех натуральных x<11. Второе выражение истинно для всех натуральных x>9 и ложно для всех натуральных x<10. Следовательно, данная импликация истинна для всех натуральных x>9. Наименьшее число, соответствующее этому условию x=10.
Ответ: 10.
задания

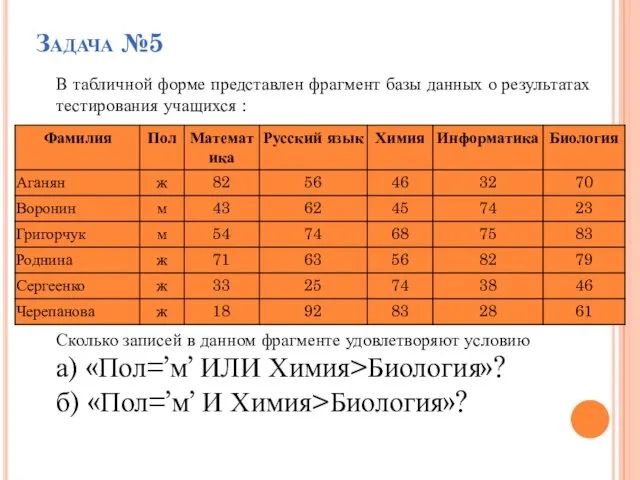
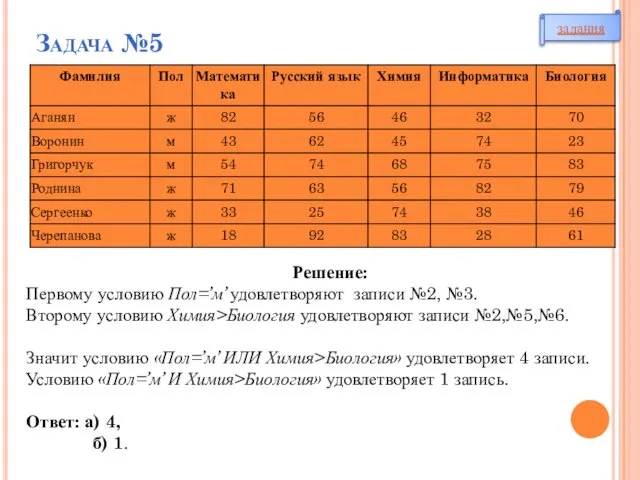
Задача №5
В табличной форме представлен фрагмент базы данных о результатах тестирования учащихся :
Сколько записей в данном фрагменте удовлетворяют условию
а) «Пол=’м’ ИЛИ Химия>Биология»?
б) «Пол=’м’ И Химия>Биология»?

Задача №5
Решение:
Первому условию Пол=’м’ удовлетворяют записи №2, №3.
Второму условию Химия>Биология удовлетворяют записи №2,№5,№6.
Значит условию «Пол=’м’ ИЛИ Химия>Биология» удовлетворяет 4 записи.
Условию «Пол=’м’ И Химия>Биология» удовлетворяет 1 запись.
Ответ: а) 4,
б) 1.
задания

Задания
1) Для какого числа X истинно высказывание:
1)1 2)3 3)4 4)2
2) Для какого числа X истинно высказывание:
1)1 2)2 3)3 4)4
3) Для какого числа X истинно высказывание:
1)1 2)2 3)3 4)4
4) Для какого числа X истинно высказывание:
1)1 2)2 3)3 4)4
5) Для какого числа X истинно высказывание:
1)1 2)2 3)3 4)4