Содержание
- 2. Архитектура Храм Ченнакесава, Сопанатапура (Индия) 1268
- 3. Изобразительное искусство Сальвадор Дали, Лицо войны, 1940
- 4. Течение жидкостей
- 5. Живая природа
- 6. Публикации
- 7. Еще публикации А. Д. Морозов, Введение в теорию фракталов, Москва-Ижевск, 2002 Andrzey Katunin, A concise introduction
- 8. Признаки фрактальных множеств Тонкая структура на всех масштабах; Нерегулярное (негладкое) строение; Самоподобие (точное, приближенное, статистическое); Дробная
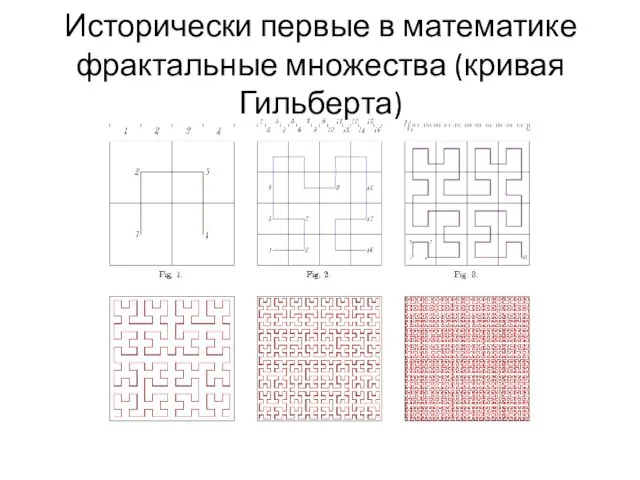
- 9. Исторически первые в математике фрактальные множества (кривая Гильберта)
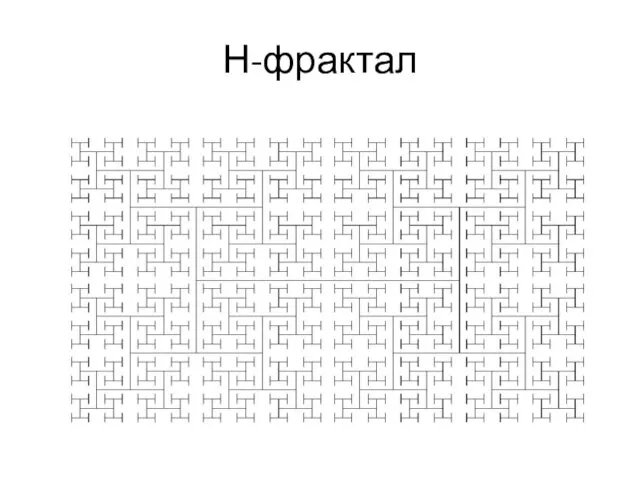
- 10. Н-фрактал
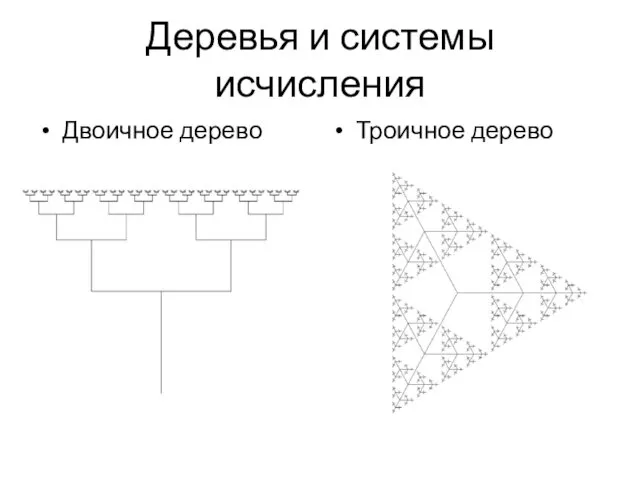
- 11. Деревья и системы исчисления Двоичное дерево Троичное дерево
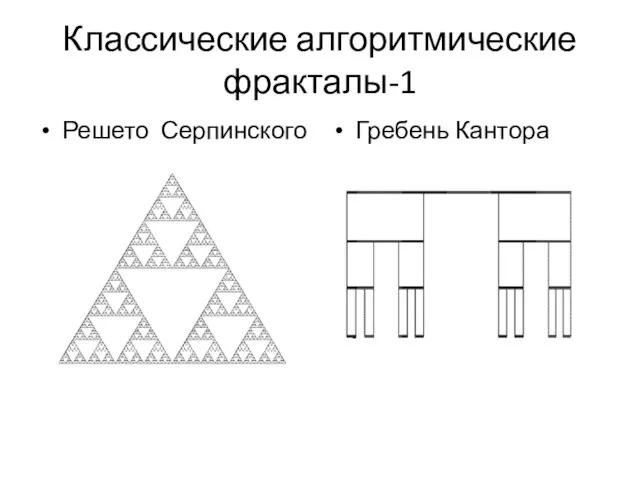
- 12. Классические алгоритмические фракталы-1 Решето Серпинского Гребень Кантора
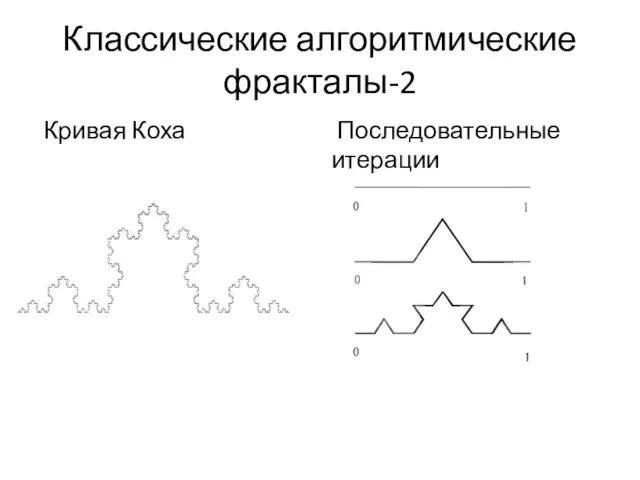
- 13. Классические алгоритмические фракталы-2 Кривая Коха Последовательные итерации
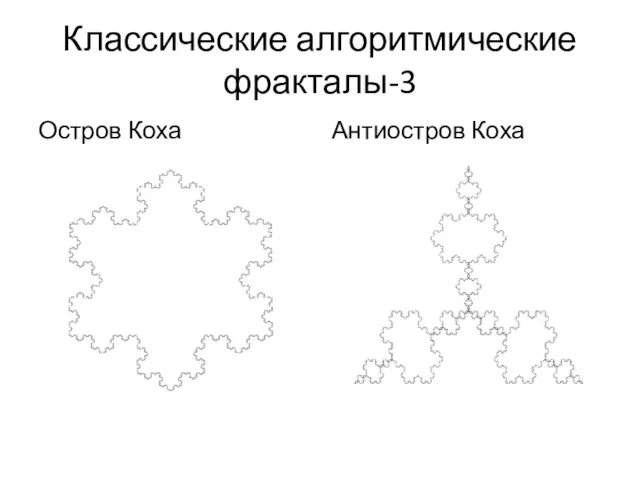
- 14. Классические алгоритмические фракталы-3 Остров Коха Антиостров Коха
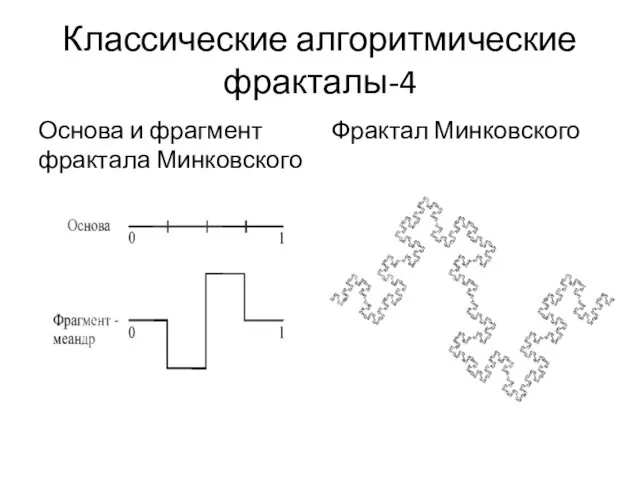
- 15. Классические алгоритмические фракталы-4 Основа и фрагмент фрактала Минковского Фрактал Минковского
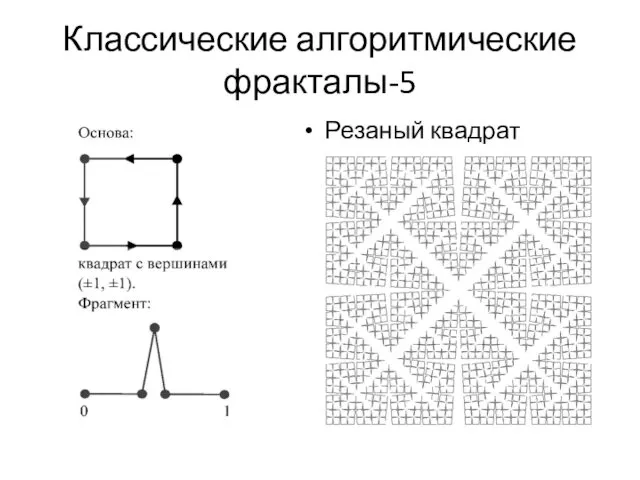
- 16. Классические алгоритмические фракталы-5 Резаный квадрат
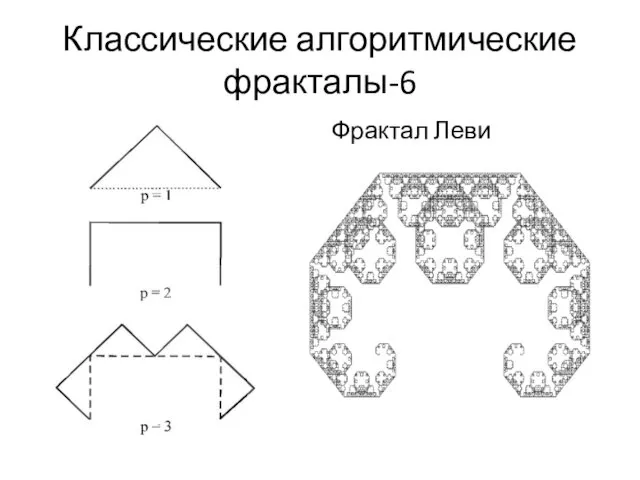
- 17. Классические алгоритмические фракталы-6 Фрактал Леви
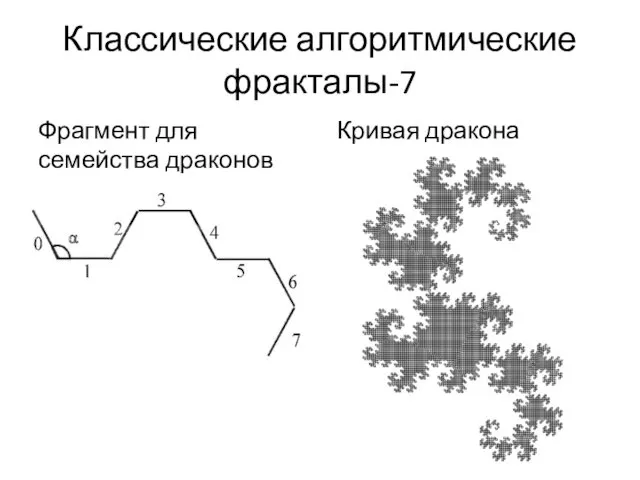
- 18. Классические алгоритмические фракталы-7 Фрагмент для семейства драконов Кривая дракона
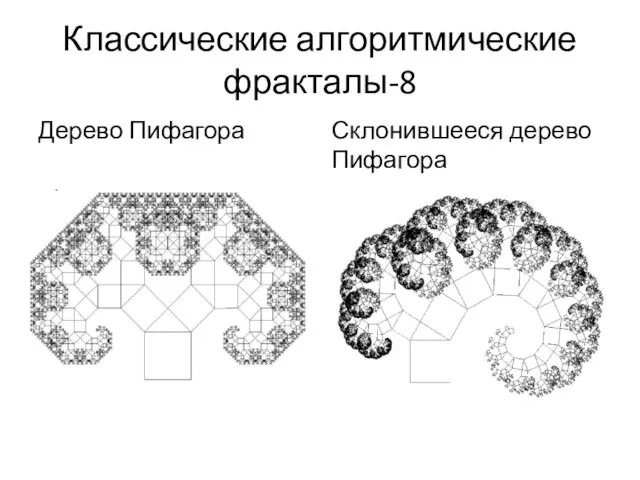
- 19. Классические алгоритмические фракталы-8 Дерево Пифагора Склонившееся дерево Пифагора
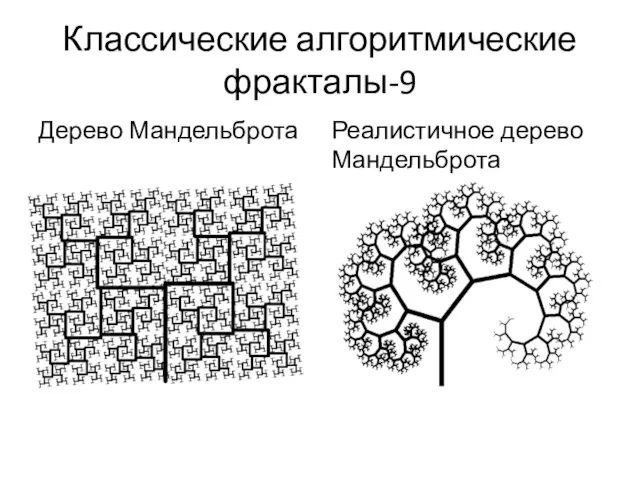
- 20. Классические алгоритмические фракталы-9 Дерево Мандельброта Реалистичное дерево Мандельброта
- 21. Общий подход Конструктивный фрактал – инвариантное множество относительно преобразований плоскости. Преобразования плоскости: вращения (R), сдвиги (T),
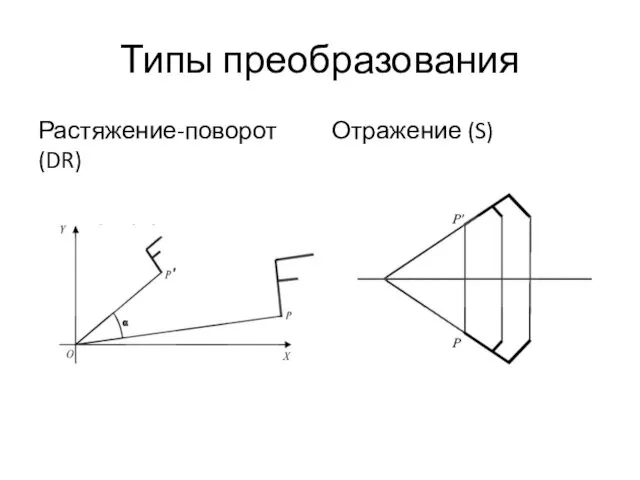
- 22. Типы преобразования Растяжение-поворот (DR) Отражение (S)
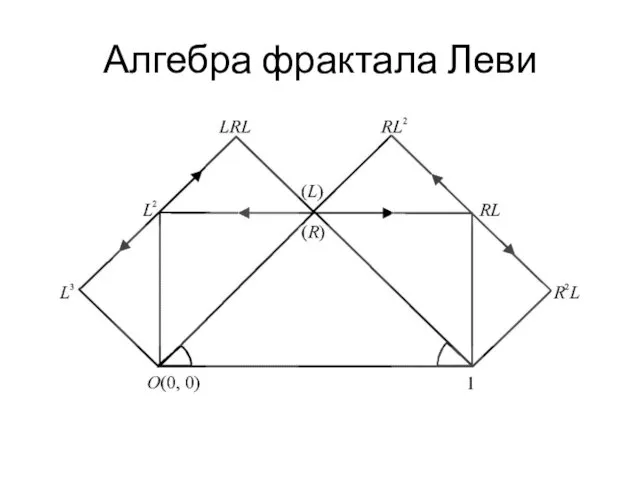
- 23. Алгебра фрактала Леви
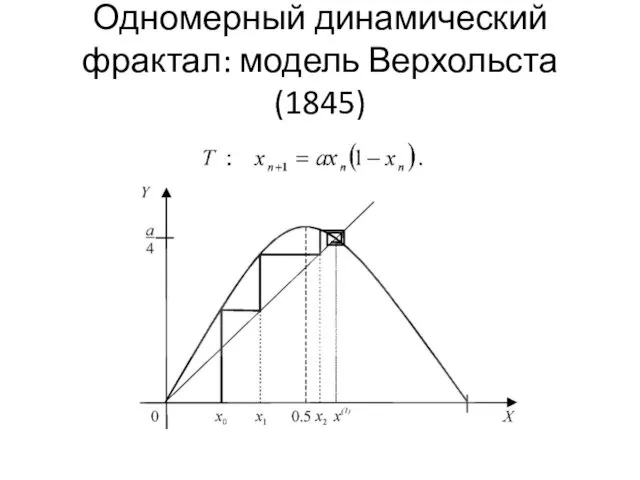
- 24. Одномерный динамический фрактал: модель Верхольста (1845)
- 25. Свойства модели Верхольста 0 1 3 3.449499
- 26. Сценарий Фейгенбаума: переход к хаосу Последовательность бифуркационных значений a сходится к по геометрической прогрессии со знаменателем:
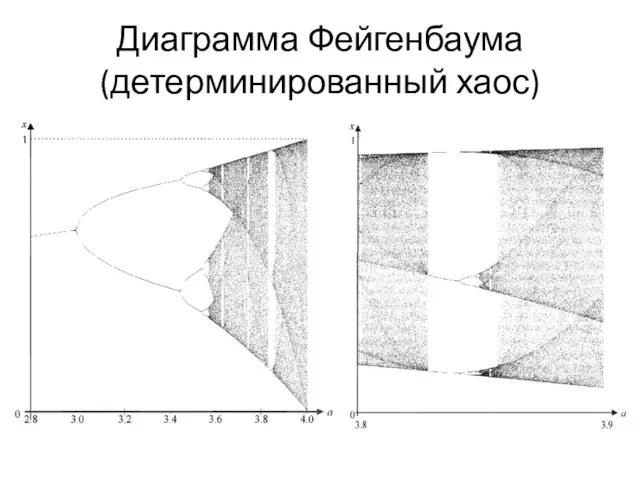
- 27. Диаграмма Фейгенбаума (детерминированный хаос)
- 28. Комплексные числа-1 (есть все 4 арифметические операции с привычными свойствами)
- 29. Комплексные числа-2
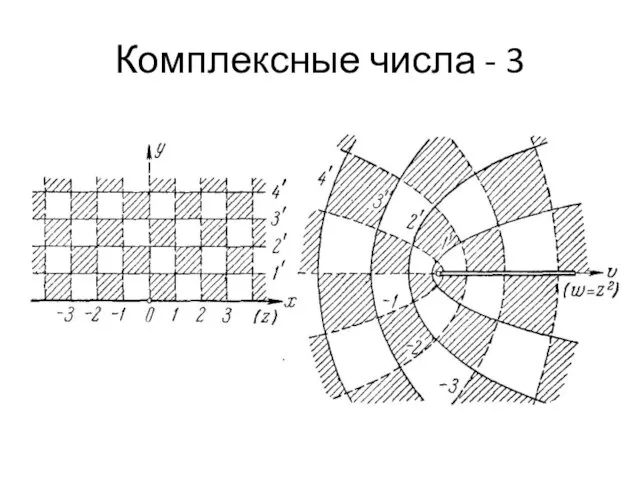
- 30. Комплексные числа - 3
- 31. Голоморфная динамика Итерации отображения (динамика в дискретном времени): Классический пример:
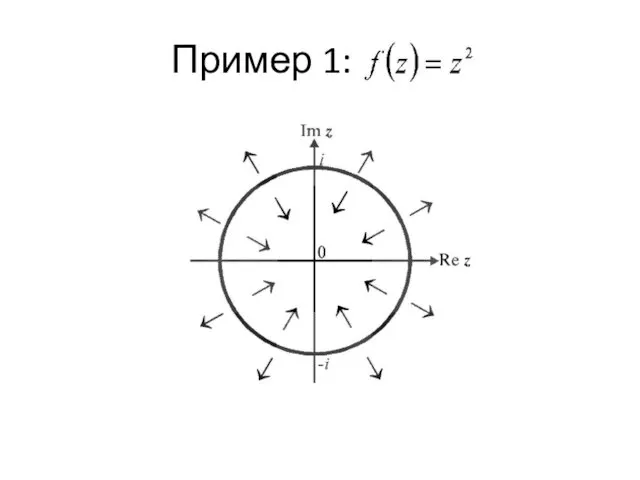
- 32. Пример 1:
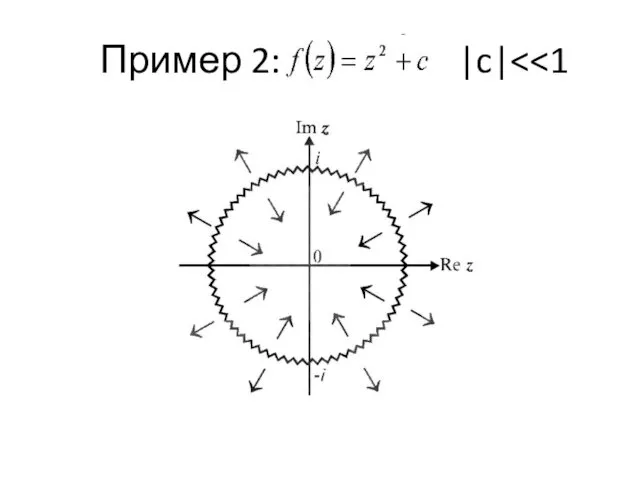
- 33. Пример 2: |c|
- 34. Общий случай Ключевой объект – циклические точки отображения: где p – наименьшее натуральное (p=1 – неподвижная
- 35. Определение множества Жюлиа J(f) замыкание множества всех отталкивающих периодических точек (замкнутый репеллер)= граница области притяжения любого
- 36. Свойства множества Жюлиа Непусто Бесконечно (несчетно) Замкнуто (содержит все пределы) Компактно (содержится внутри некоторого круга) Не
- 37. Пример множества Жюлиа
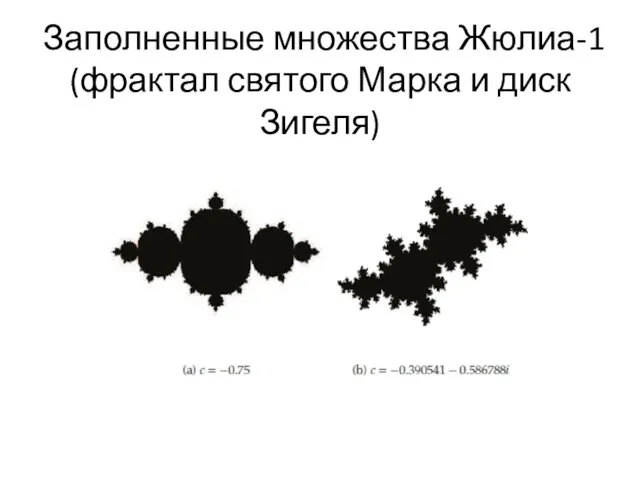
- 38. Заполненные множества Жюлиа-1 (фрактал святого Марка и диск Зигеля)
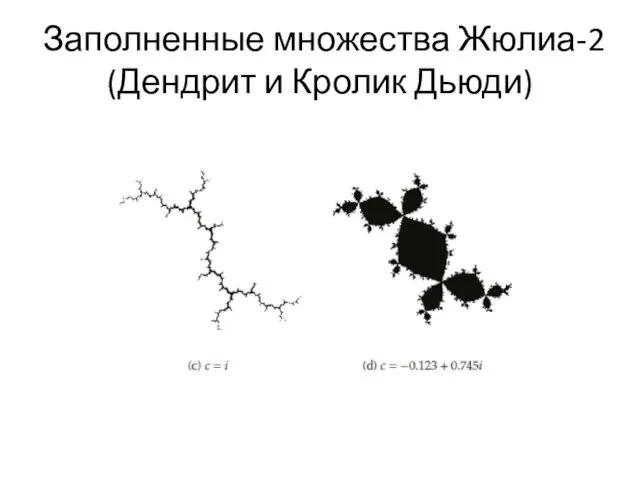
- 39. Заполненные множества Жюлиа-2 (Дендрит и Кролик Дьюди)
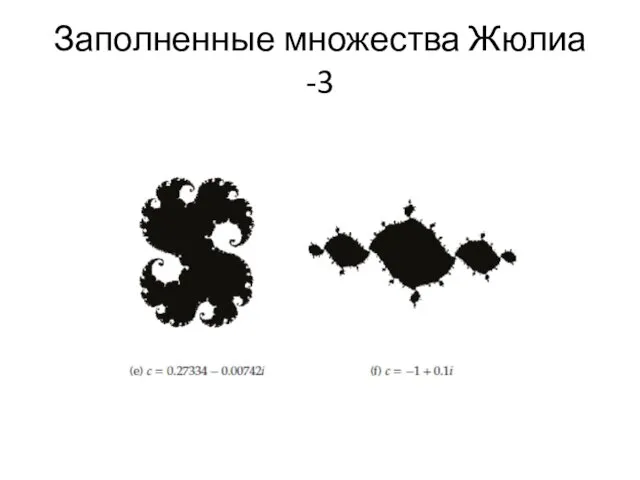
- 40. Заполненные множества Жюлиа -3
- 41. Раскрашенные фракталы
- 42. Полиномиальные множества Жюлиа и Фату: , 0≤p≤1 p=0 – постоянное отображение, с – устойчивая неподвижная точка,
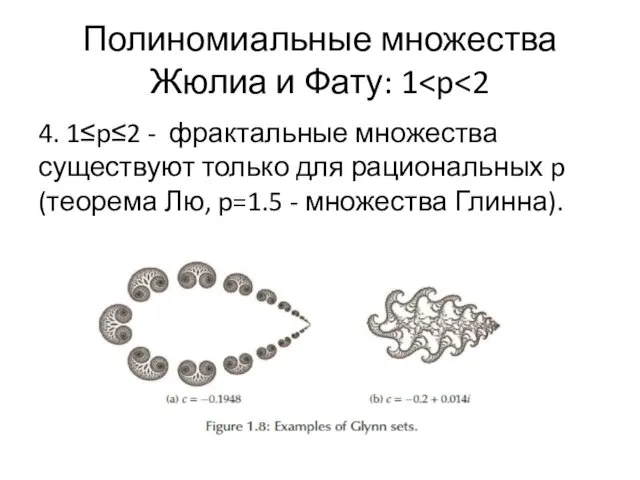
- 43. Полиномиальные множества Жюлиа и Фату: 1 4. 1≤p≤2 - фрактальные множества существуют только для рациональных p
- 44. Полиномиальные множества Жюлиа и Фату: p=3
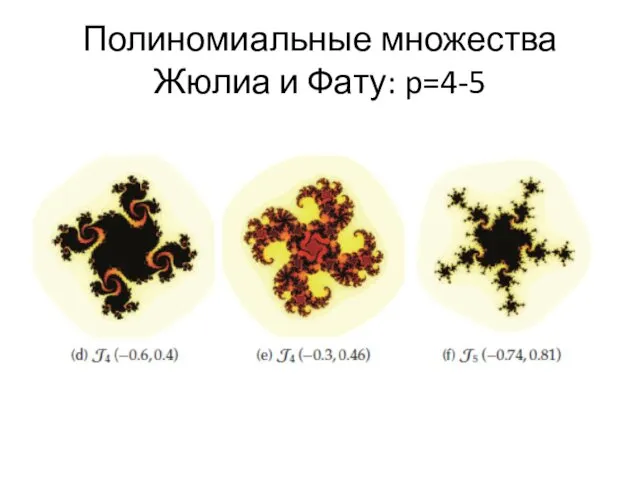
- 45. Полиномиальные множества Жюлиа и Фату: p=4-5
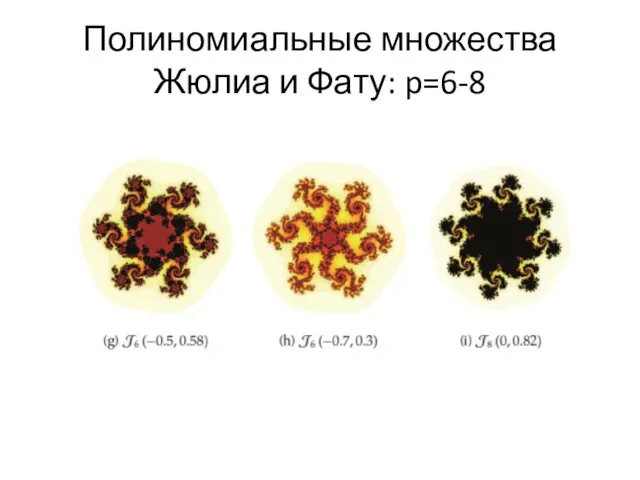
- 46. Полиномиальные множества Жюлиа и Фату: p=6-8
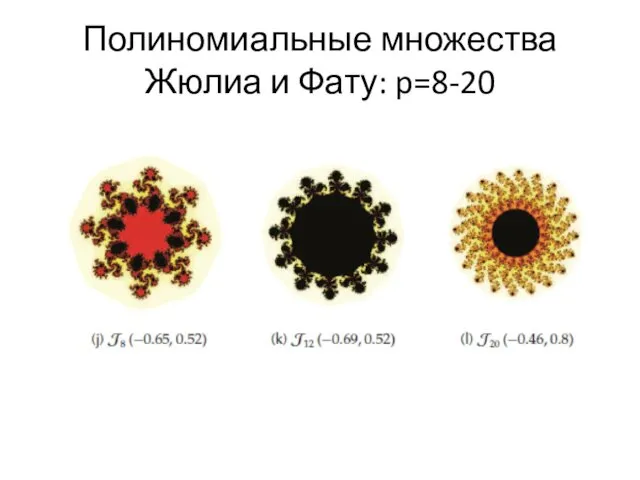
- 47. Полиномиальные множества Жюлиа и Фату: p=8-20
- 48. Полиномиальные множества Жюлиа и Фату: p→∞
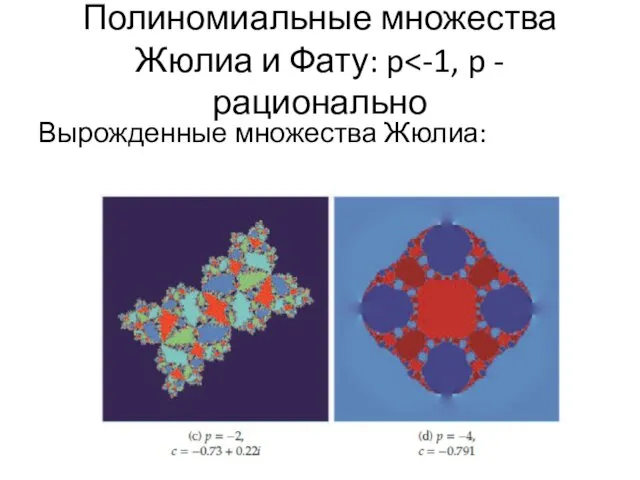
- 49. Полиномиальные множества Жюлиа и Фату: p Вырожденные множества Жюлиа:
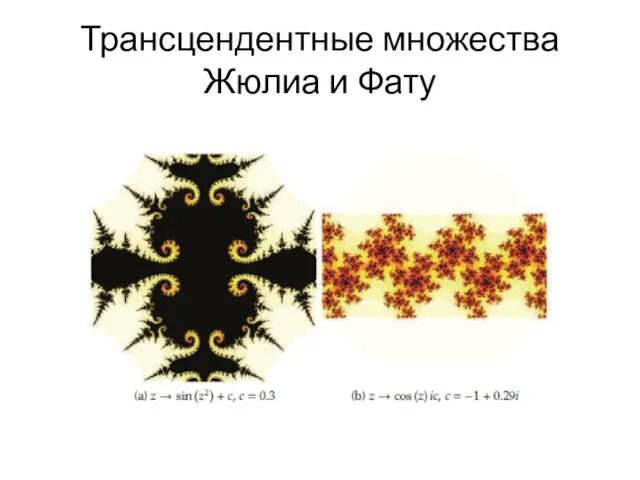
- 50. Трансцендентные множества Жюлиа и Фату
- 51. Трансцендентные множества Жюлиа и Фату
- 52. Что такое фрактал Мандельброта? Множество (фрактал) Мандельброта M – это множество значений комплексного параметра с, при
- 53. Фрактал Мандельброта
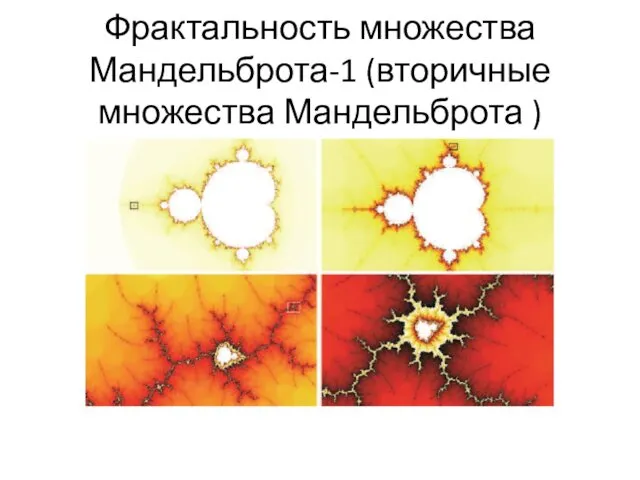
- 54. Фрактальность множества Мандельброта-1 (вторичные множества Мандельброта )
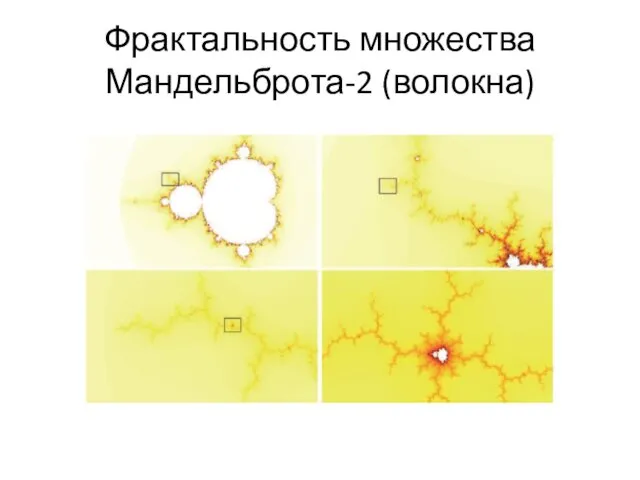
- 55. Фрактальность множества Мандельброта-2 (волокна)
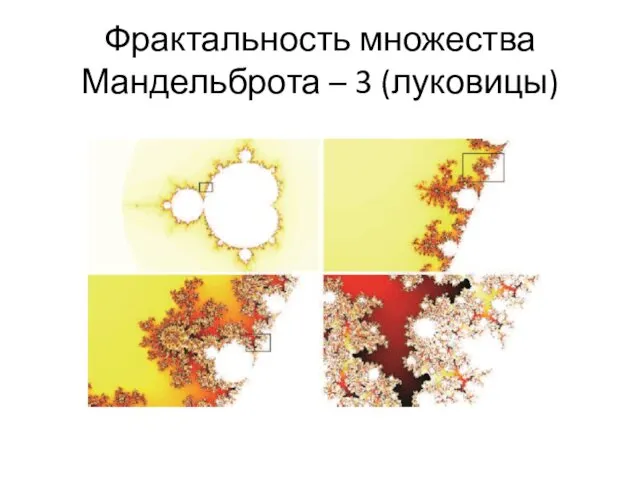
- 56. Фрактальность множества Мандельброта – 3 (луковицы)
- 57. Фрактальность множества Мандельброта – 4 (Долина Морских Коньков)
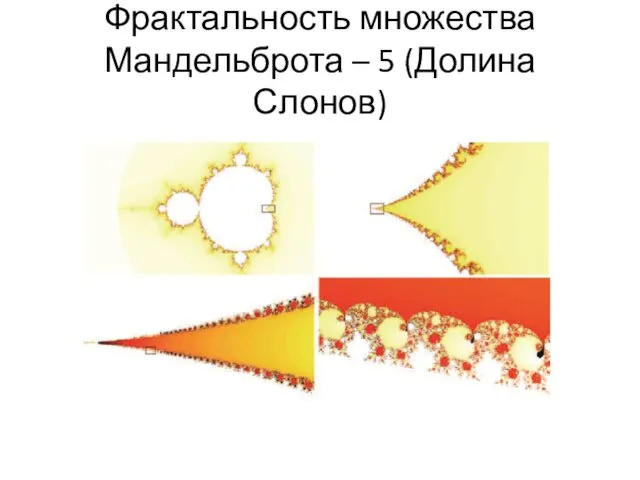
- 58. Фрактальность множества Мандельброта – 5 (Долина Слонов)
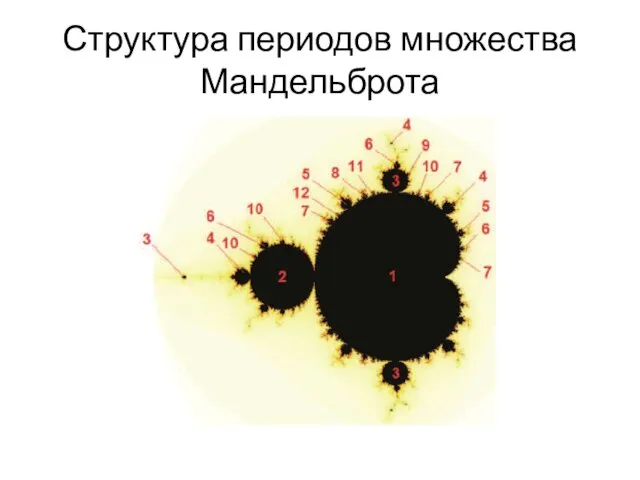
- 59. Структура периодов множества Мандельброта
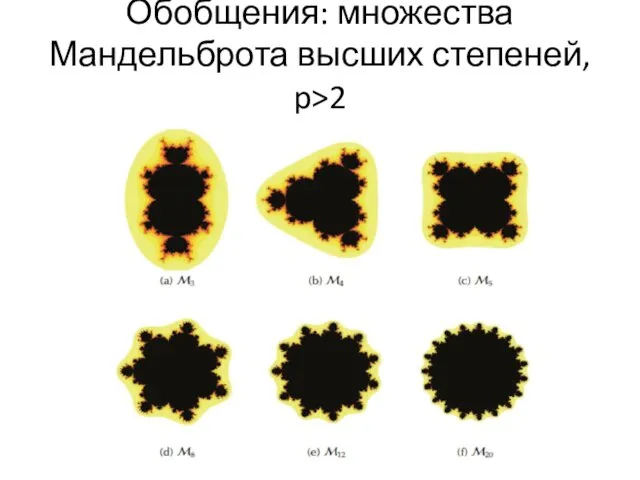
- 60. Обобщения: множества Мандельброта высших степеней, p>2
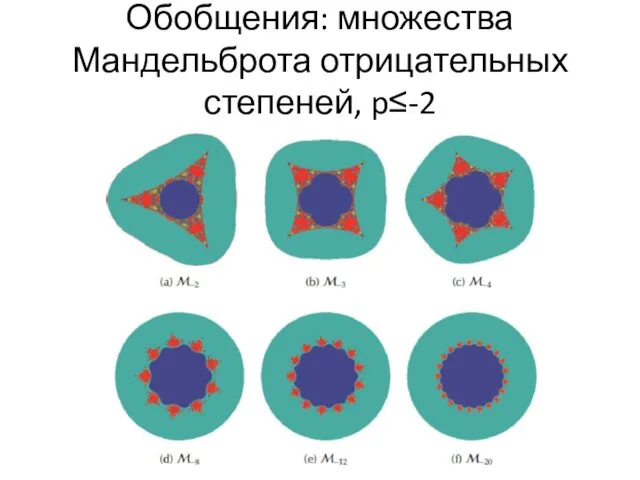
- 61. Обобщения: множества Мандельброта отрицательных степеней, p≤-2
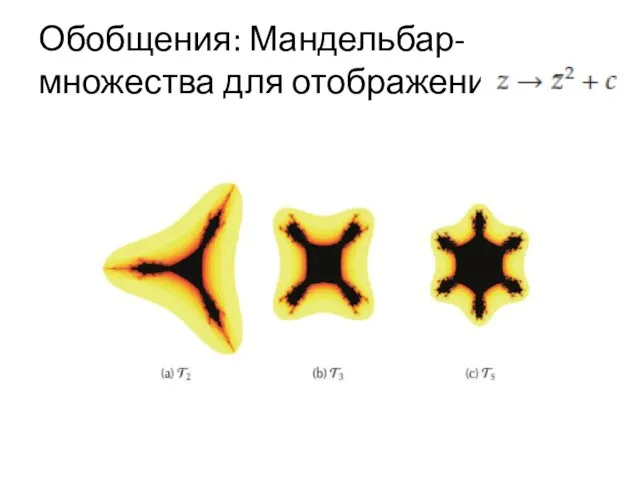
- 62. Обобщения: Мандельбар-множества для отображения
- 63. Дальнейшие обобщения: возможны ли 3-мерные множества Мандельброта и Жюлиа? Даниэл Уйат, 2007 (неалгебраический 3-мерный аналог голоморфной
- 64. Обобщение Ниландера: Мандельбалбы
- 65. Жюлиа-балбы
- 66. Мандельбоксы (3D Мандельбары)
- 67. Кватернионы (Гамильтон, 1843)
- 68. Кватернионные множества Жюлиа: 3-мерные проекции
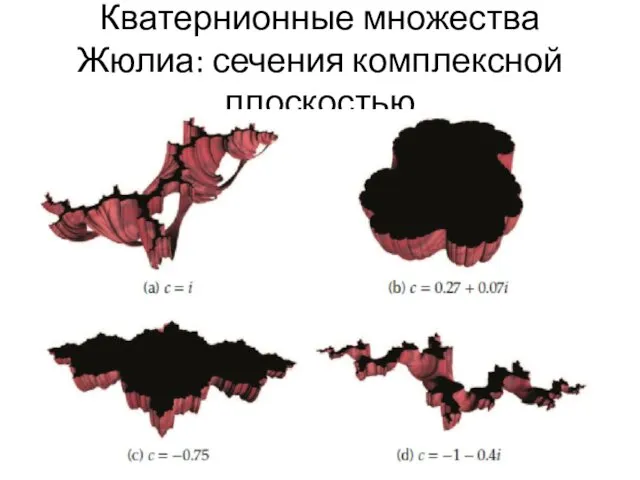
- 69. Кватернионные множества Жюлиа: сечения комплексной плоскостью
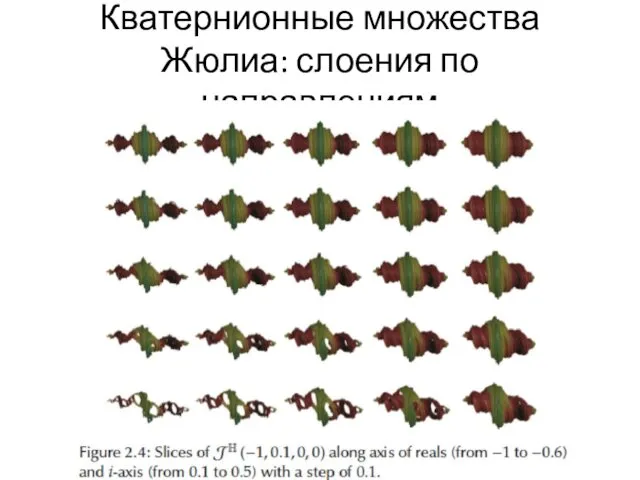
- 70. Кватернионные множества Жюлиа: слоения по направлениям
- 71. Кватернионное множество Мандельброта: 3-мерная проекция
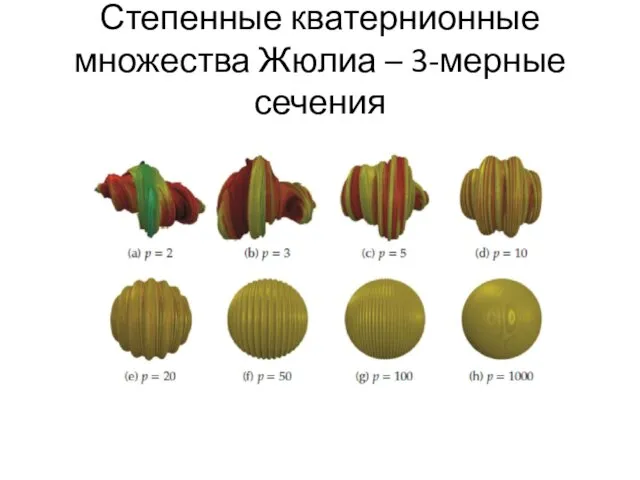
- 72. Степенные кватернионные множества Жюлиа – 3-мерные сечения
- 73. Обобщенно-полиномиальные кватернионные множества Жюлиа
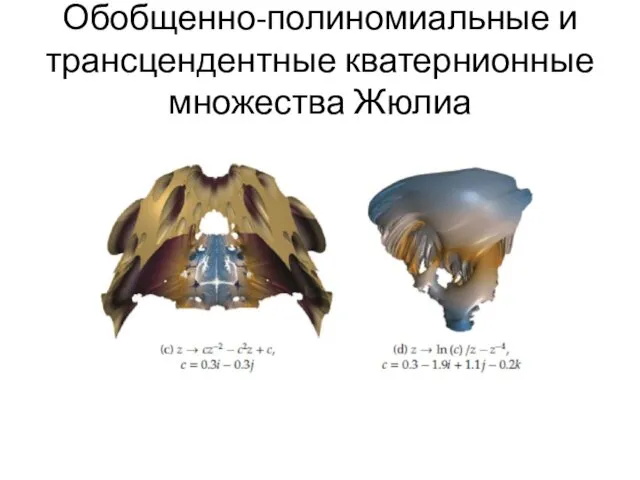
- 74. Обобщенно-полиномиальные и трансцендентные кватернионные множества Жюлиа
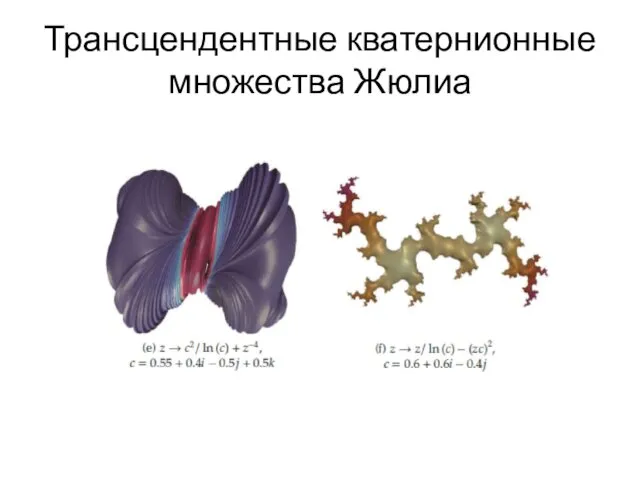
- 75. Трансцендентные кватернионные множества Жюлиа
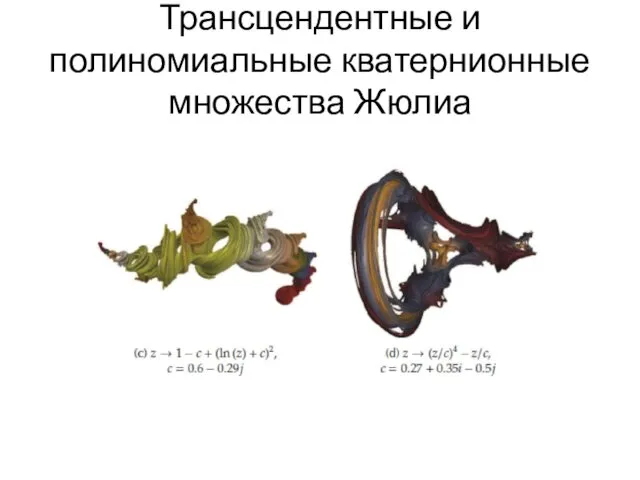
- 76. Трансцендентные и полиномиальные кватернионные множества Жюлиа
- 77. Трансцендентные и полиномиальные кватернионные множества Жюлиа
- 78. Трансцендентные кватернионные множества Жюлиа
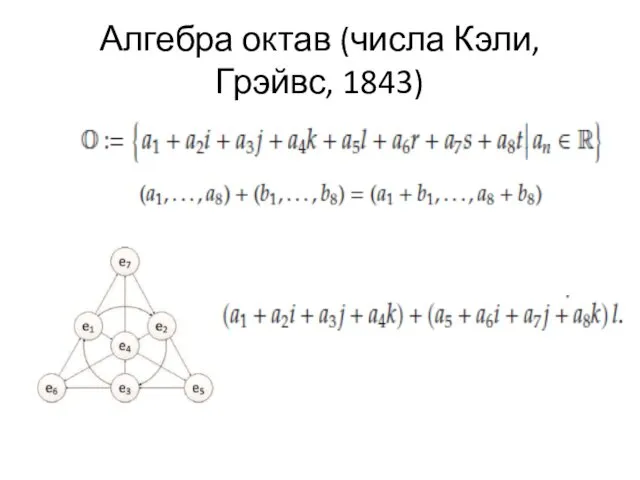
- 79. Алгебра октав (числа Кэли, Грэйвс, 1843)
- 80. Итерационный процесс над октавами Неассоциативность Проблема визуализации
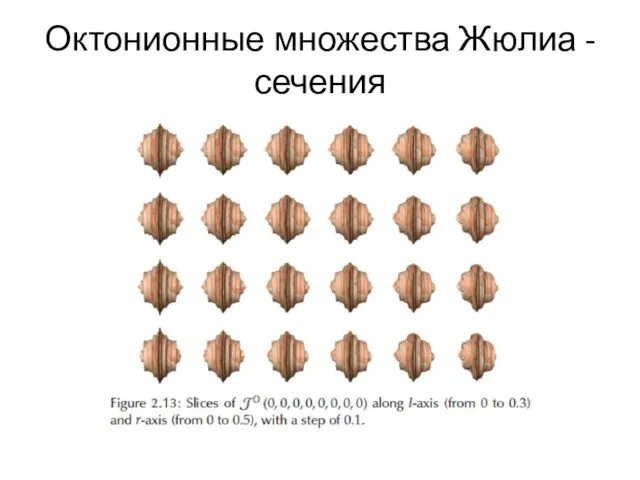
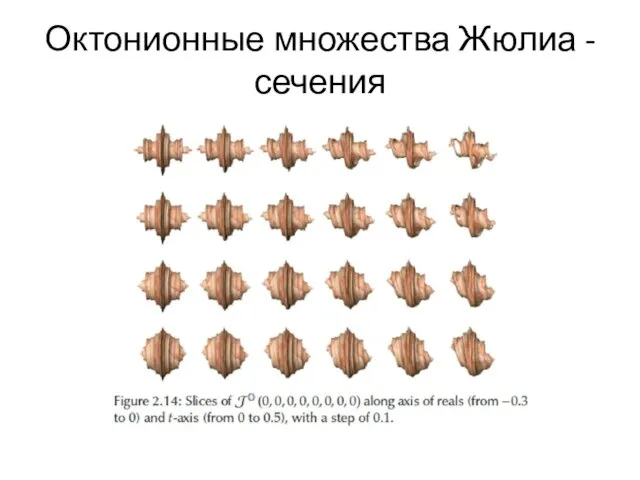
- 81. Октонионные множества Жюлиа - сечения
- 82. Октонионные множества Жюлиа - сечения
- 83. Октонионные множества Жюлиа - сечения
- 84. Что дальше: сединионы, патионы? R,C,H,O – нормированные алгебры с делением (других нет); S,P,… - (размерность 16,
- 85. Алгебры Клиффорда
- 86. Клиффордовы фрактальные множества
- 87. «Фракталы» на двойных и дуальных числах: a+bj (jj=+1, jj=0)
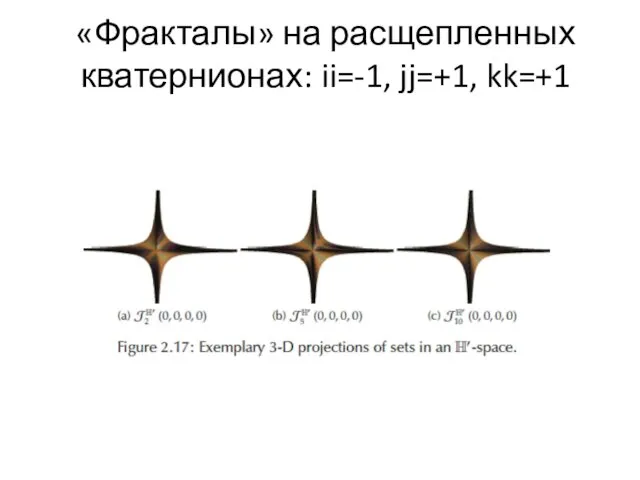
- 88. «Фракталы» на расщепленных кватернионах: ii=-1, jj=+1, kk=+1
- 89. «Фракталы» на полукватернионах: ii=-1, jj=kk=jk=0
- 90. Действительно ли невозможны фракталы на двойных числах? Алгебра двойных чисел: a+bj, jj=+1 Ассоциативно-коммутативна; Содержит делители нуля;
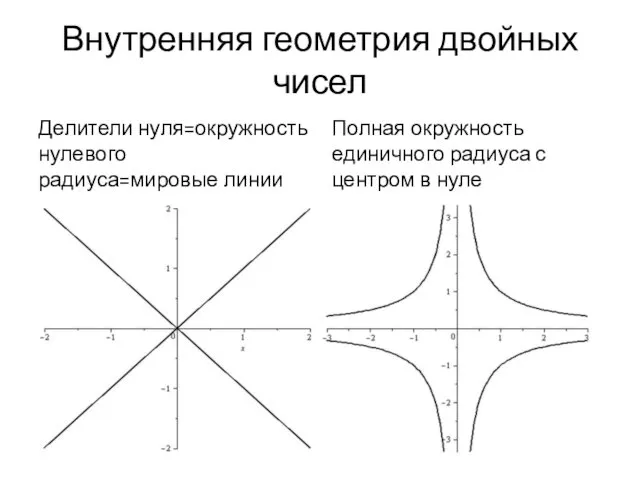
- 91. Внутренняя геометрия двойных чисел Делители нуля=окружность нулевого радиуса=мировые линии света Полная окружность единичного радиуса с центром
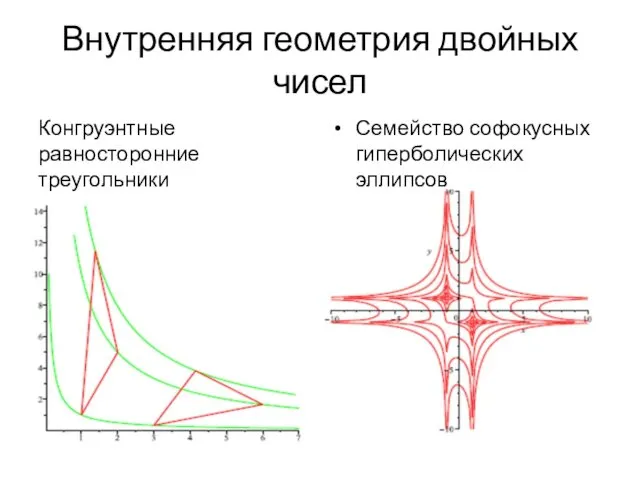
- 92. Внутренняя геометрия двойных чисел Конгруэнтные равносторонние треугольники Семейство софокусных гиперболических эллипсов
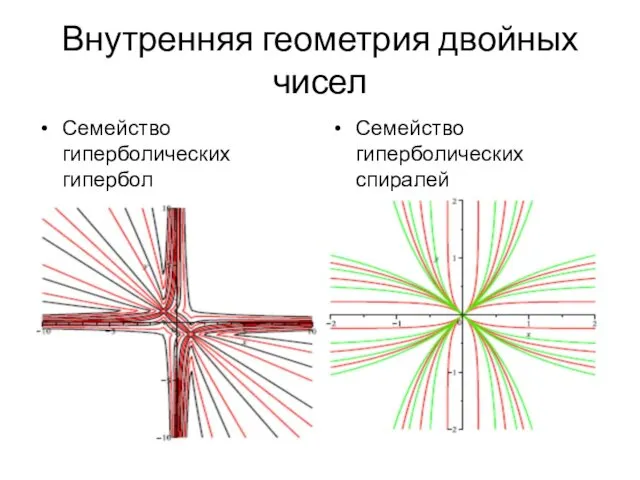
- 93. Внутренняя геометрия двойных чисел Семейство гиперболических гипербол Семейство гиперболических спиралей
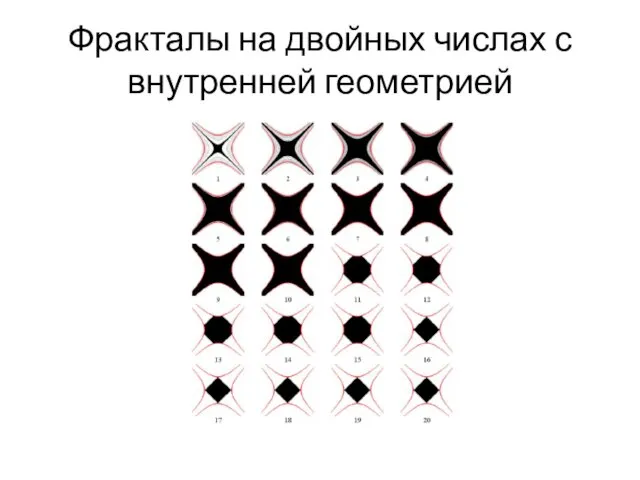
- 94. Фракталы на двойных числах с внутренней геометрией
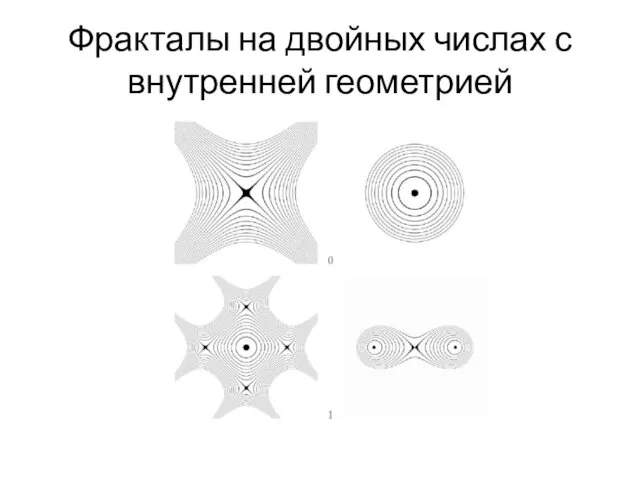
- 95. Фракталы на двойных числах с внутренней геометрией
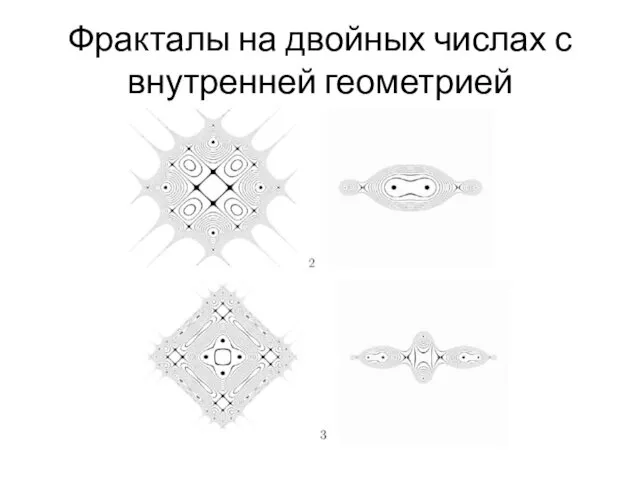
- 96. Фракталы на двойных числах с внутренней геометрией
- 97. Фракталы на двойных числах с внутренней геометрией
- 98. Фракталы на двойных числах с внутренней геометрией
- 99. Публикации
- 100. Алгебраический конструктор: прямая сумма алгебр и тензорное произведение
- 101. Бикомплексные числа (тессарины)
- 102. Бикомплексные множества Жюлиа (проекции)
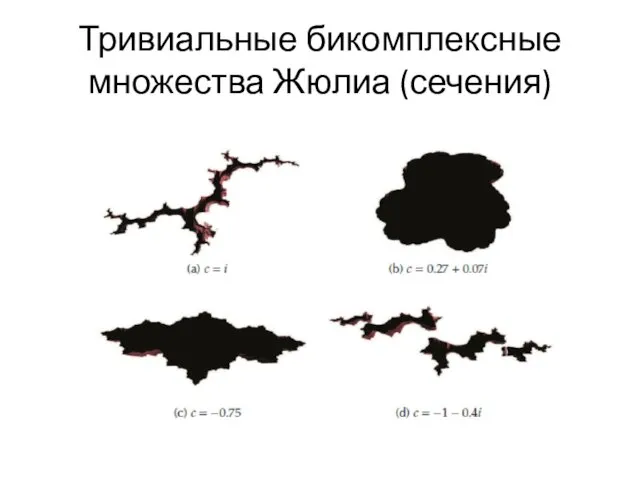
- 103. Тривиальные бикомплексные множества Жюлиа (сечения)
- 104. Полиномиальные бикомплексные множества Жюлиа
- 105. Предел полиномиальных бикомплексных множеств Жюлиа – тело Штейнмеца
- 106. Слоения бикомплексного множества Жюлиа
- 107. Проекция бикомплексного множества Мандельброта (Тетраброт)
- 108. Бикватернионы
- 109. Несвязные бикватернионные множества Жюлиа
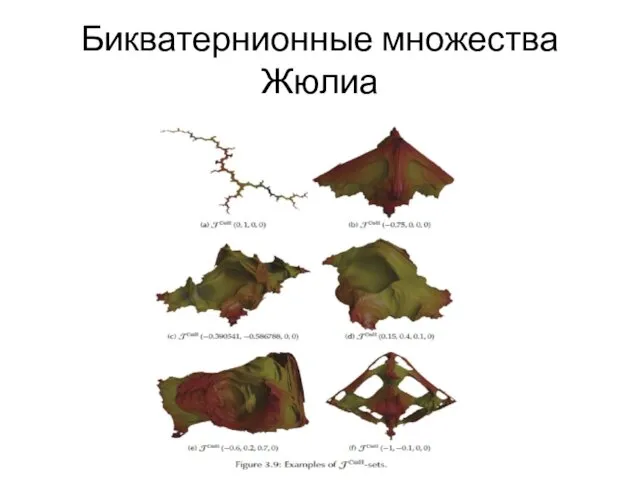
- 110. Бикватернионные множества Жюлиа
- 111. Полиномиальные бикватернионные множества Жюлиа
- 112. Слоения бикватернионного множества Жюлиа
- 114. Скачать презентацию

























































 Appearance & Personality Activities
Appearance & Personality Activities Методы обеспечения точности сборки
Методы обеспечения точности сборки Элементы математической статистики, комбинаторики и теории вероятности.Решение задач из вариантов ЕГЭ.
Элементы математической статистики, комбинаторики и теории вероятности.Решение задач из вариантов ЕГЭ. Урок по теме Волны в океане 6 класс
Урок по теме Волны в океане 6 класс Дымковская игрушка
Дымковская игрушка Региональные мероприятия РДШ Воронежской области
Региональные мероприятия РДШ Воронежской области Дифференциация звуков [л - р]
Дифференциация звуков [л - р] Курсовая работа по теории государства и права
Курсовая работа по теории государства и права Разработка туристического продукта Краткосрочный корпоративный круиз для судоходных компаний
Разработка туристического продукта Краткосрочный корпоративный круиз для судоходных компаний matematika_2_e_perimetr
matematika_2_e_perimetr История связи. Интернет
История связи. Интернет Чрез тернии к звёздам
Чрез тернии к звёздам Сущность понятия Педагогическая технология и его научные аспекты
Сущность понятия Педагогическая технология и его научные аспекты Весна, паводок
Весна, паводок Визитка класса
Визитка класса Отчёт по работе Духовно-просветительского центра Глазовской епархии за 2019 год
Отчёт по работе Духовно-просветительского центра Глазовской епархии за 2019 год Методическое и техническое обеспечение учебного процесса по информатике
Методическое и техническое обеспечение учебного процесса по информатике Автоматизация звука [л'] в чистоговорках
Автоматизация звука [л'] в чистоговорках Окружающая человека среда и ее компоненты
Окружающая человека среда и ее компоненты Сущность человека. Биологическое и социальное в человеке
Сущность человека. Биологическое и социальное в человеке Архитектура персонального компьютера
Архитектура персонального компьютера Организация работы первичных трудовых коллективов
Организация работы первичных трудовых коллективов Нефть.Проклятие или благодать?
Нефть.Проклятие или благодать? Особливості таравлення у жуйних
Особливості таравлення у жуйних Сенсорное развитие дошкольников в познавательнопрактической деятельности
Сенсорное развитие дошкольников в познавательнопрактической деятельности Алгоритм изучения дисциплины Философия
Алгоритм изучения дисциплины Философия Правила пожарной безопасности дома 2 класс 8(2)
Правила пожарной безопасности дома 2 класс 8(2) презентация оксиды на службе у художников(1)
презентация оксиды на службе у художников(1)