Содержание
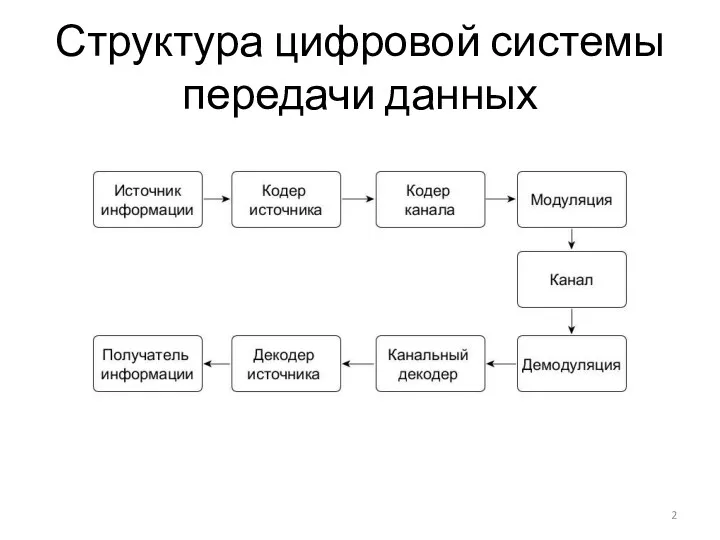
- 2. Структура цифровой системы передачи данных
- 3. Предел Шеннона (теорема Шеннона — Хартли) К.Шеннон «РАБОТЫ ПО ТЕОРИИ ИНФОРМАЦИИ И КИБЕРНЕТИКЕ», ИЗДАТЕЛЬСТВО ИНОСТРАННОЙ ЛИТЕРАТУРЫ,
- 4. Предел Шеннона
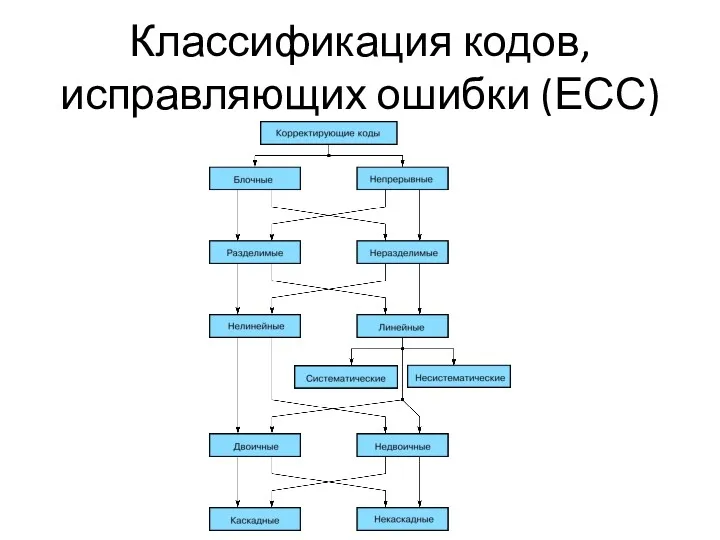
- 5. Классификация кодов, исправляющих ошибки (ЕСС)
- 6. Классификация кодов, исправляющих ошибки (ЕСС) Наиболее многочисленный класс разделимых кодов составляют линейные коды. Основная их особенность
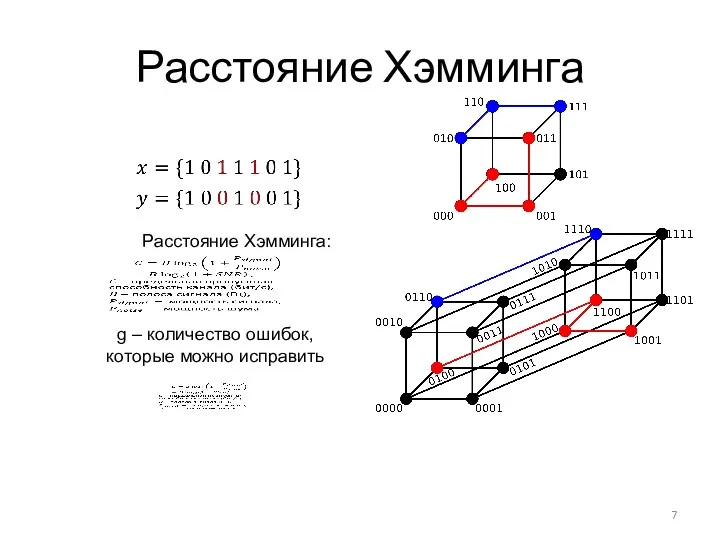
- 7. Расстояние Хэмминга Расстояние Хэмминга: g – количество ошибок, которые можно исправить
- 8. Код Хемминга
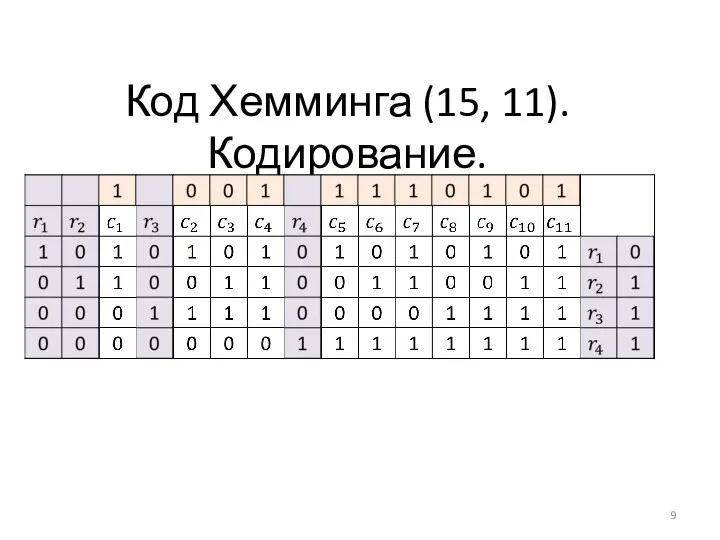
- 9. Код Хемминга (15, 11). Кодирование.
- 10. Код Хемминга (15, 11). Декодирование.
- 11. Идея кодирования. Проверка четности.
- 12. Идея кодирования. Код повторения.
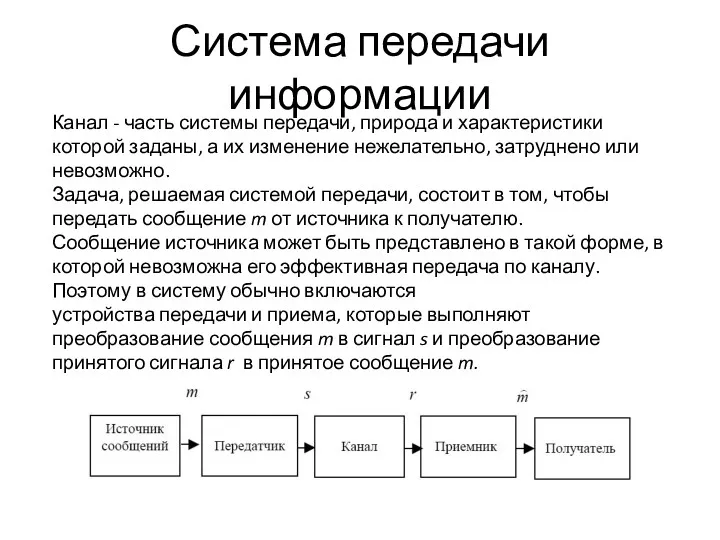
- 13. Система передачи информации Канал - часть системы передачи, природа и характеристики которой заданы, а их изменение
- 14. Общие сведения Если источник порождает сообщения из конечного множества, то он называется источником дискретных сообщений, в
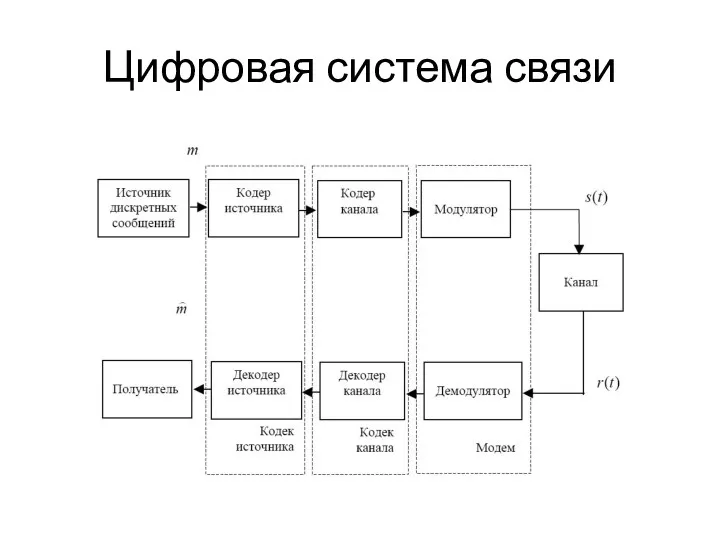
- 15. Цифровая система связи
- 16. Общие сведения Канальное, или помехоустойчивое, кодирование-декодирование применяется для обеспечения большей надежности передачи. При использовании помехоустойчивого кодирования
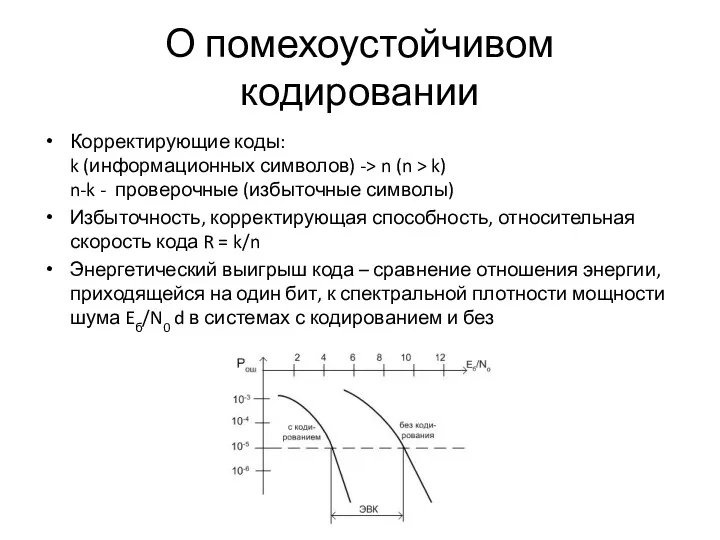
- 17. О помехоустойчивом кодировании Корректирующие коды: k (информационных символов) -> n (n > k) n-k - проверочные
- 18. О помехоустойчивом кодировании
- 19. О помехоустойчивом кодировании
- 20. Блоковое кодирование
- 21. Блоковое кодирование
- 22. Блоковое кодирование
- 23. Блоковое кодирование
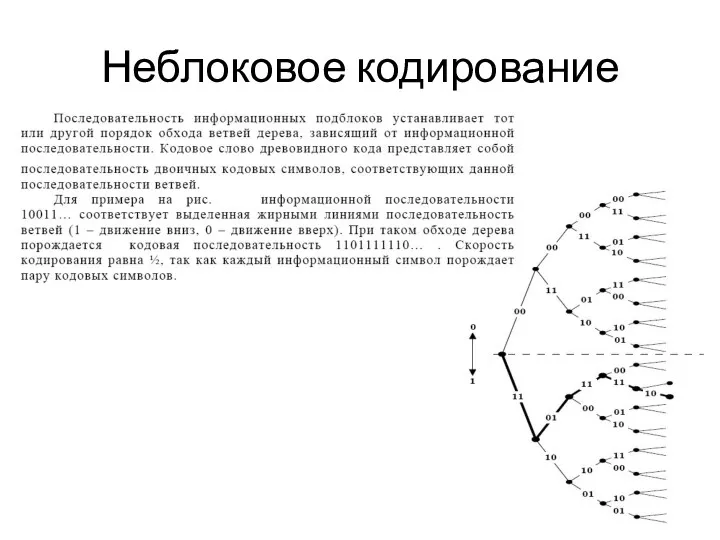
- 24. Неблоковое кодирование
- 25. Неблоковое кодирование
- 26. Неблоковое кодирование
- 27. Классификация кодов, исправляющих ошибки (ЕСС) В соответствии с этой классификацией корректирующие коды делятся на две группы:
- 28. Классификация кодов, исправляющих ошибки (ЕСС) Отличительной особенностью непрерывных кодов является то, что обработка поступающих символов производится
- 29. Корректирующие коды, используемые в системах ЦТВ Блоковые Рида-Соломона БЧХ LDPC Сверточные (кодовое ограничение К – количество
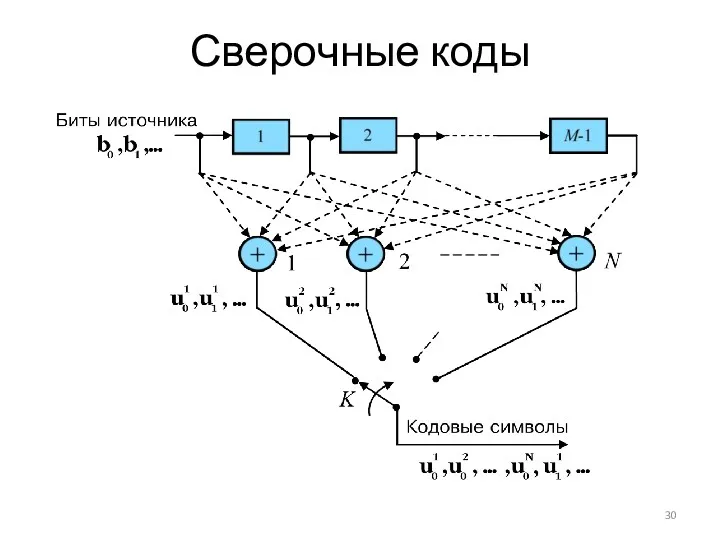
- 30. Сверочные коды
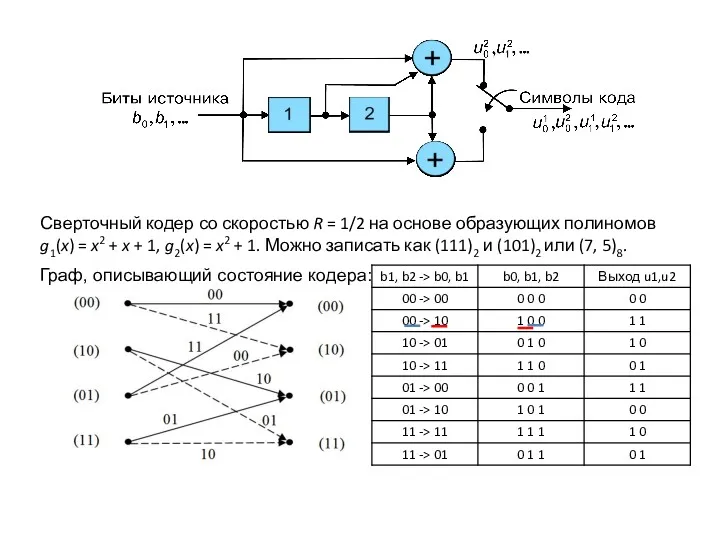
- 31. Сверточный кодер со скоростью R = 1/2 на основе образующих полиномов g1(x) = x2 + x
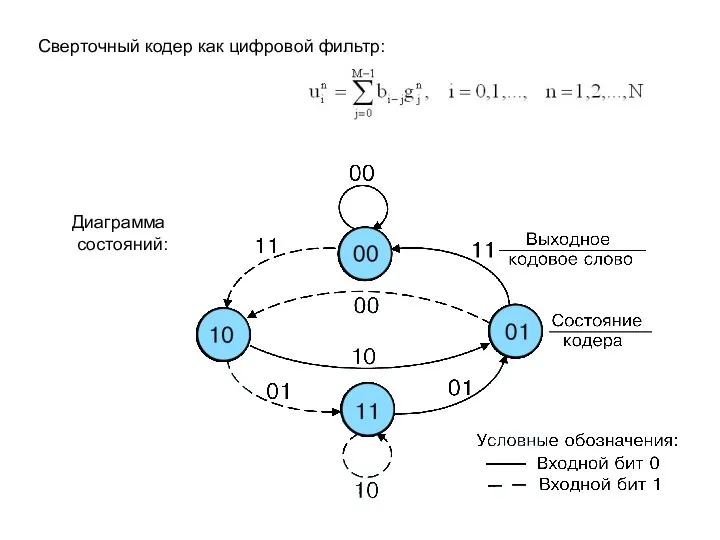
- 32. Сверточный кодер как цифровой фильтр: Диаграмма состояний:
- 33. Граф, описывающий состояние кодера: входная информационная последовательность {bi}=10100100 отображается в кодовое слово {ui1,ui2}=11 10 00 10
- 34. Декодирование сверточных кодов Алгоритм Витерби На i–м шаге декодирования, в течение которого принимается i–я n–символьная кодовая
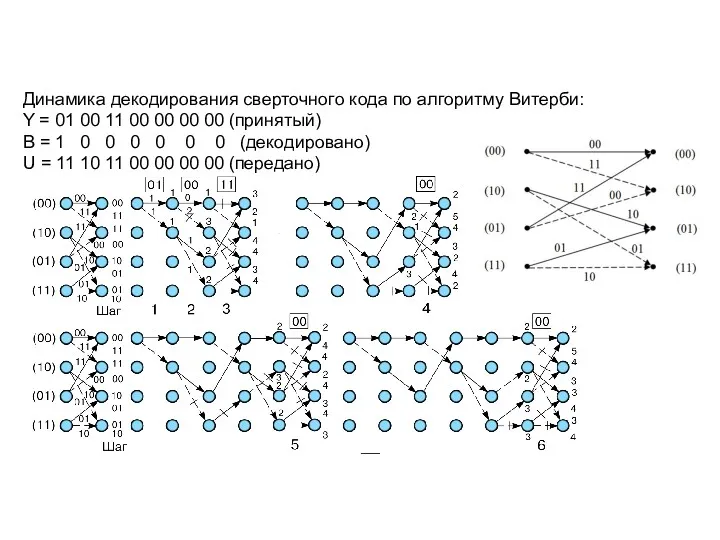
- 35. Динамика декодирования сверточного кода по алгоритму Витерби: Y = 01 00 11 00 00 00 00
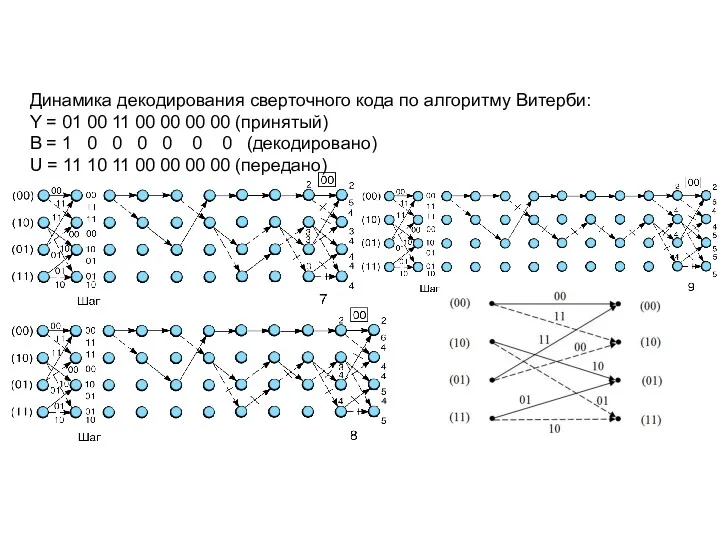
- 36. Динамика декодирования сверточного кода по алгоритму Витерби: Y = 01 00 11 00 00 00 00
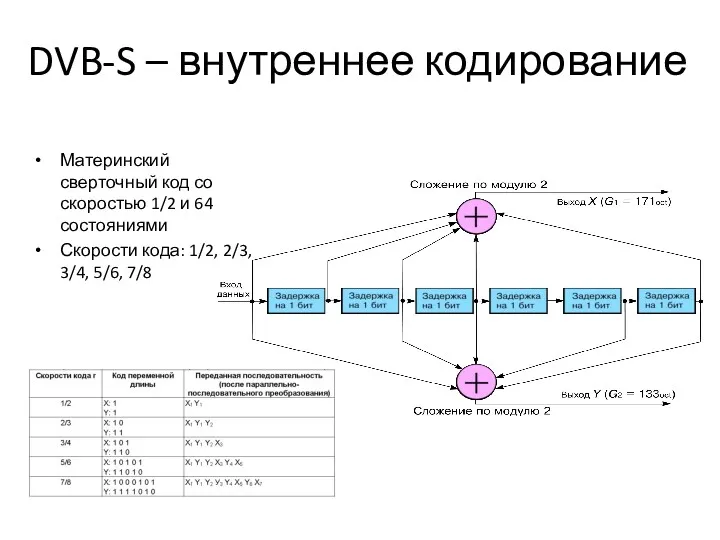
- 37. DVB-S – внутреннее кодирование Материнский сверточный код со скоростью 1/2 и 64 состояниями Скорости кода: 1/2,
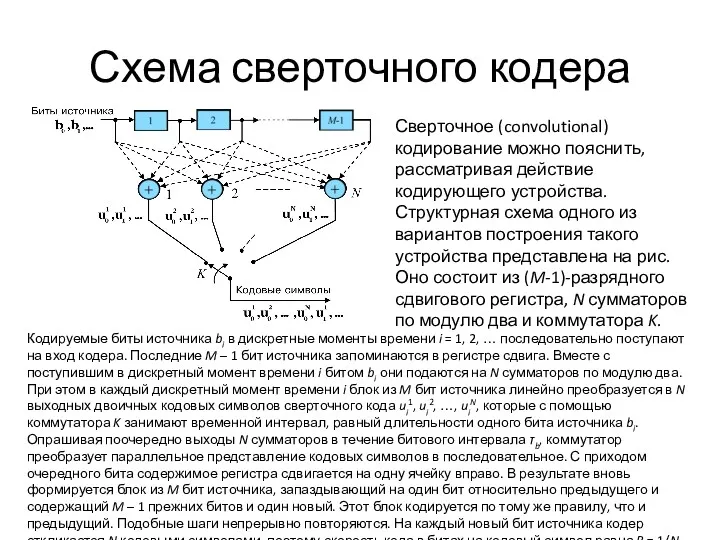
- 38. Схема сверточного кодера Сверточное (convolutional) кодирование можно пояснить, рассматривая действие кодирующего устройства. Структурная схема одного из
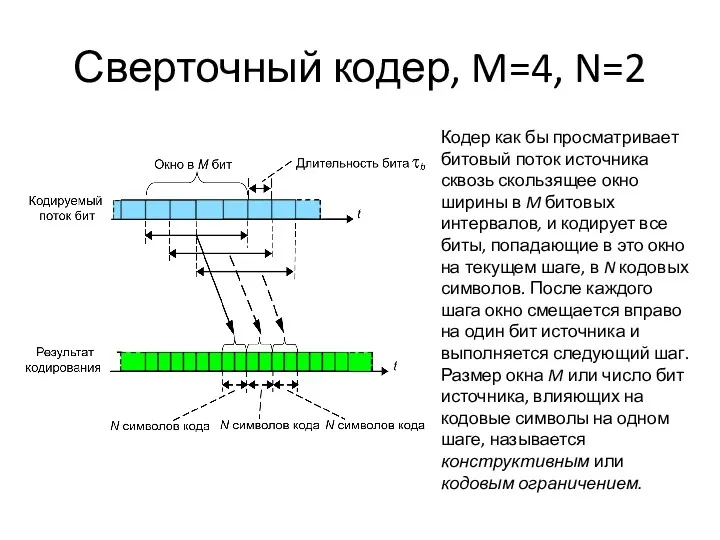
- 39. Сверточный кодер, M=4, N=2 Кодер как бы просматривает битовый поток источника сквозь скользящее окно ширины в
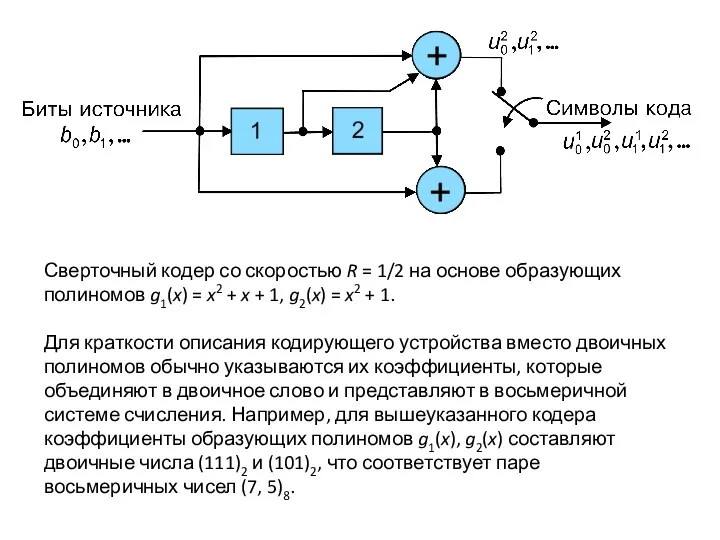
- 40. Сверточный кодер со скоростью R = 1/2 на основе образующих полиномов g1(x) = x2 + x
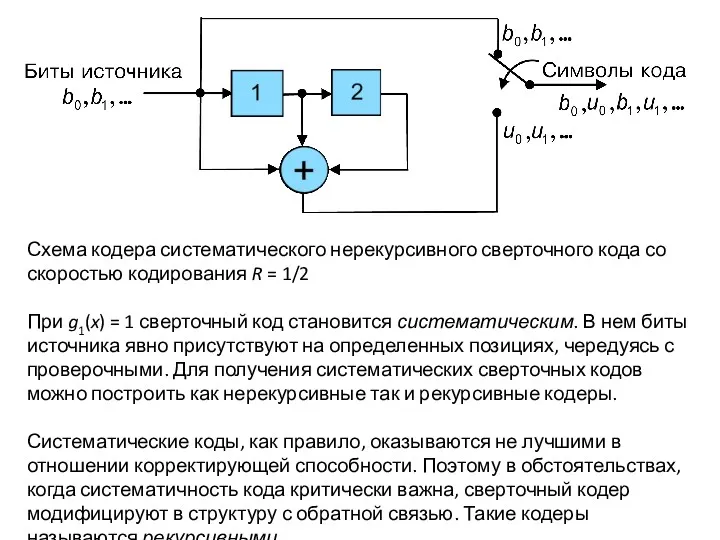
- 41. Схема кодера систематического нерекурсивного сверточного кода со скоростью кодирования R = 1/2 При g1(x) = 1
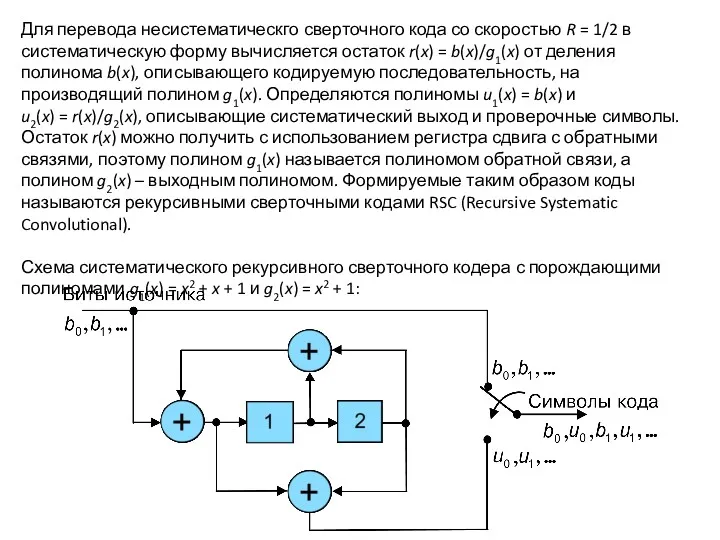
- 42. Для перевода несистематическго сверточного кода со скоростью R = 1/2 в систематическую форму вычисляется остаток r(x)
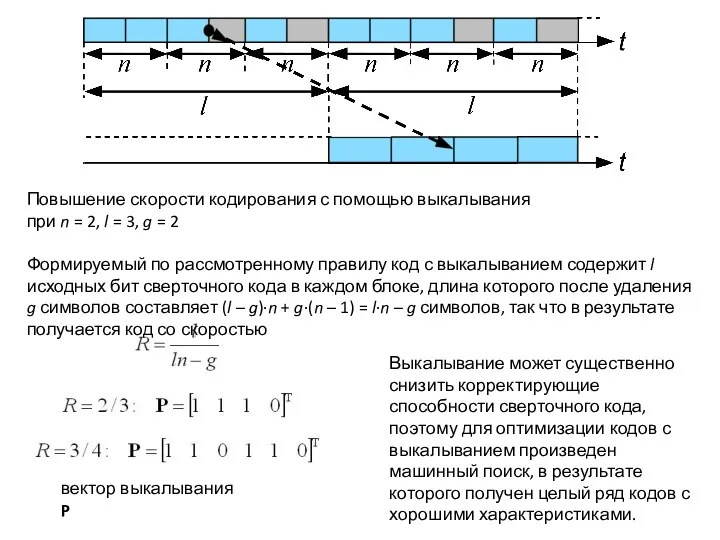
- 43. При использовании сверточных кодов со скоростью R = 1/N наибольшая кодовая скорость равна 1/2. Во многих
- 44. Выкалывание может существенно снизить корректирующие способности сверточного кода, поэтому для оптимизации кодов с выкалыванием произведен машинный
- 45. Порождающая и проверочная матрицы кода Пусть С – двоичный линейный код (n, k, dmin) Любое кодовое
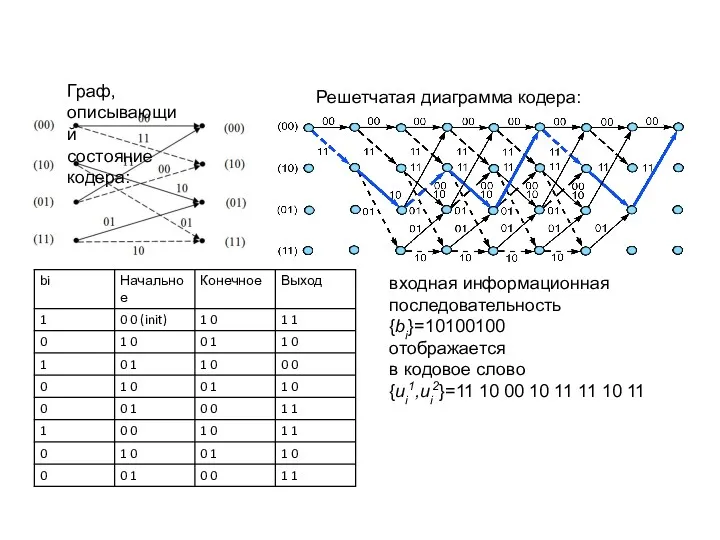
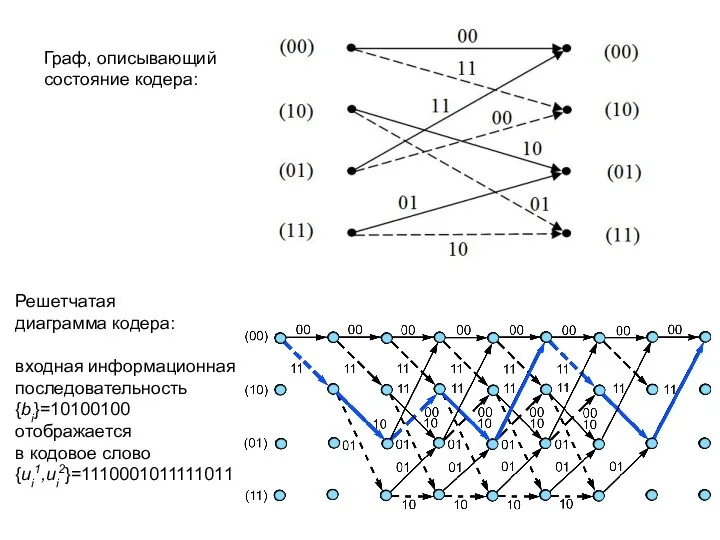
- 46. Граф, описывающий состояние кодера: Решетчатая диаграмма кодера: входная информационная последовательность {bi}=10100100 отображается в кодовое слово {ui1,ui2}=1110001011111011
- 47. Декодирование сверточных кодов Алгоритм Витерби Алгоритм Витерби является оптимальным, он обеспечивает максимально правдоподобное решение и сводится
- 48. Декодирование сверточных кодов Алгоритм Витерби На i–м шаге декодирования, в течение которого принимается i–я n–символьная кодовая
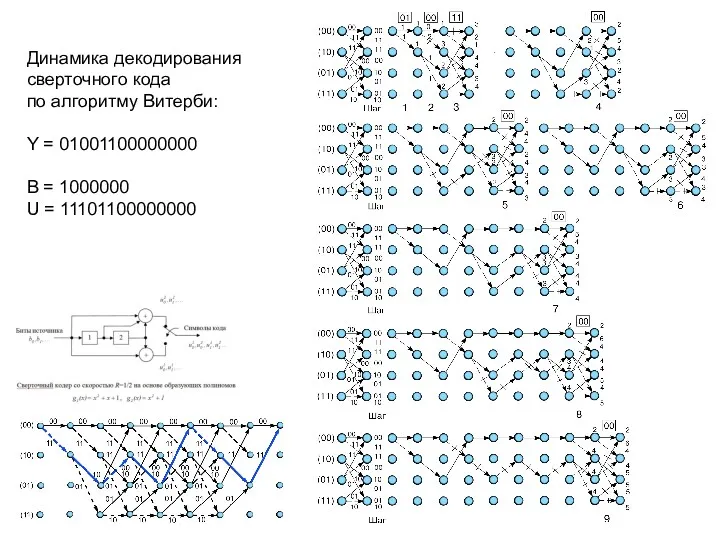
- 49. Динамика декодирования сверточного кода по алгоритму Витерби: Y = 01001100000000 B = 1000000 U = 11101100000000
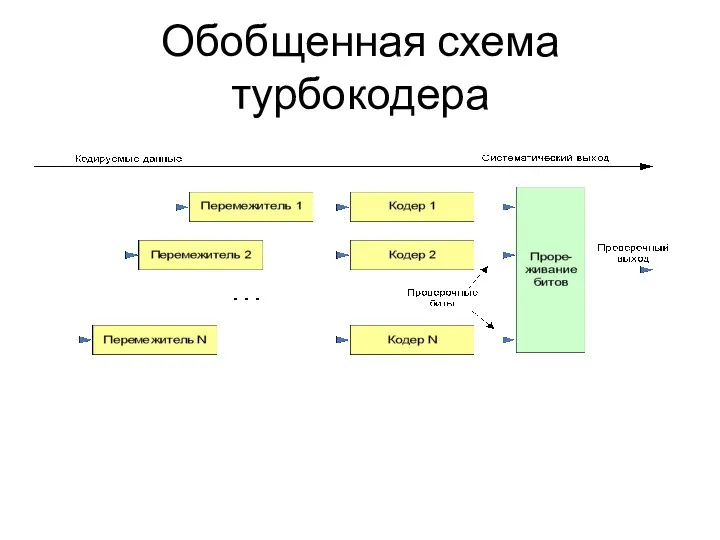
- 50. Обобщенная схема турбокодера
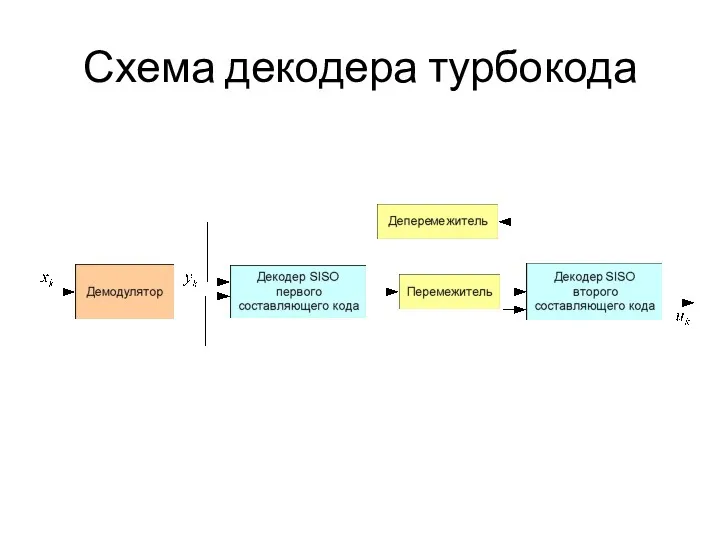
- 51. Схема декодера турбокода
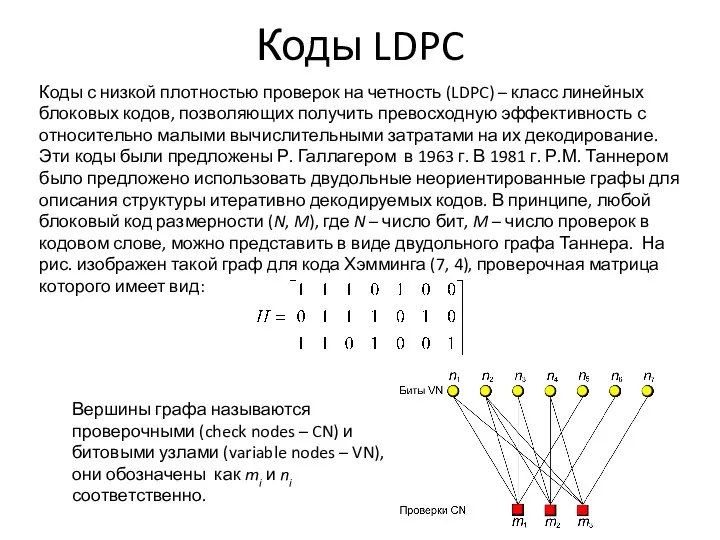
- 52. Коды LDPC Коды с низкой плотностью проверок на четность (LDPC) – класс линейных блоковых кодов, позволяющих
- 53. Коды LDPC При помощи графа Таннера большинство алгоритмов декодирования LDPC кодов можно представить в виде процесса
- 54. Классификация кодов LDPC По определению, данному Р. Галлагером, код LDPC – это линейный код, проверочная матрица
- 55. Классификация кодов LDPC К недостаткам циклических кодов можно отнести фиксированный для всех скоростей кодирования размер проверочной
- 56. Методы построения проверочных матриц кодов LDPC Методы построения LDPC кодов также можно разбить на классы. К
- 57. LDPC коды Галлагера Проверочная матрица кода строится из подматриц Ha, a = 1, …, dc, которые
- 58. LDPC коды Галлагера Пример циклов кратности 4: Рассмотренный алгоритм не гарантирует отсутствие циклов кратности 4, однако
- 59. LDPC коды МакКея Тридцать пять лет спустя МакКей, будучи незнакомым с работой Галлагера, повторно открыл преимущества
- 60. LDPC коды повторения накопления К настоящему времени разработано достаточно большое количество более сложных алгоритмов, позволяющих получать
- 61. LDPC коды повторения накопления Код DVB‑T2 является нерегулярным – степени символьных вершин переменные, в то время
- 62. LDPC коды повторения накопления Из структуры рассмотренного графа Таннера видно, что проверочную матрицу кода можно представить
- 63. LDPC коды повторения накопления Можно показать, что операция умножения на матрицу эквивалента накоплению результата в простейшем
- 64. LDPC коды DVB-T2 Используемые в DVB-T2 проверочные матрицы LDPC кода, помимо того, что они описывают IRA
- 65. LDPC коды DVB-T2 Для полного описания структуры матрицы используемого кода необходимо указать проверочные узлы, соединенные с
- 66. Декодирование кодов LDPC Р. Галлагер предложил два итеративных алгоритма декодирования кодов LDPC. Первый – алгоритм с
- 67. Декодирование кодов LDPC - BF Алгоритм BF можно представить в виде основных шагов, выполняемых итеративно: -
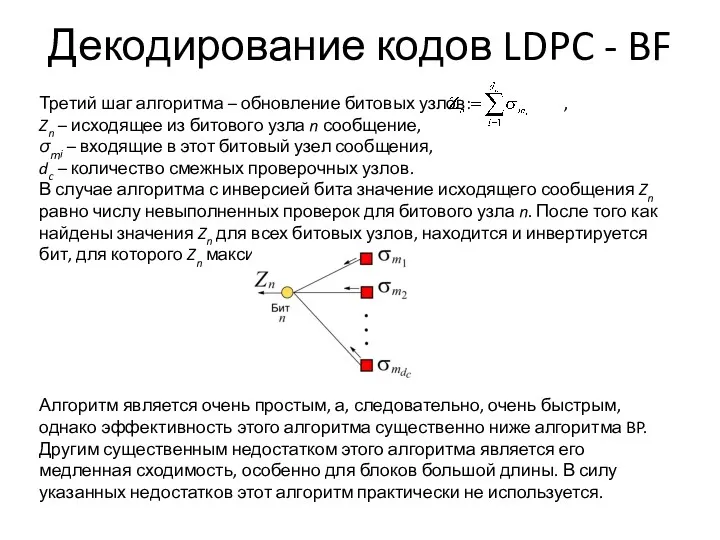
- 68. Декодирование кодов LDPC - BF Третий шаг алгоритма – обновление битовых узлов: , Zn – исходящее
- 69. Декодирование кодов LDPC - BP Алгоритм BP можно представить в виде следующих шагов: - инициализация, -
- 70. Декодирование кодов LDPC - BP Третий шаг – обновление битовых узлов: ynmi – входящие сообщения для
- 72. Скачать презентацию










































 Конструктивные особенности высотных зданий
Конструктивные особенности высотных зданий Фонарик из цветной бумаги и картона
Фонарик из цветной бумаги и картона Классификация мебели
Классификация мебели Презентация Масленница
Презентация Масленница Вербное воскресение. Пасха
Вербное воскресение. Пасха Возрождение религии. Ислам как культура мира
Возрождение религии. Ислам как культура мира Говори чисто, обучение грамоте, 1 класс
Говори чисто, обучение грамоте, 1 класс Облачные технологии
Облачные технологии klass
klass Кавказская война. Имам Шамиль (26 июня 1797 – 16 февраля 1871)
Кавказская война. Имам Шамиль (26 июня 1797 – 16 февраля 1871) Назначение, общее устройство, тактико-технические характеристики навигационного оборудования
Назначение, общее устройство, тактико-технические характеристики навигационного оборудования Презинтация Вредные привычки
Презинтация Вредные привычки Судебная практика. Качели. Возмещение вреда
Судебная практика. Качели. Возмещение вреда Организация внутреннего пространства
Организация внутреннего пространства Как получить дом вместо однушки
Как получить дом вместо однушки AWADA - комфортное освещение с полным контролем и оптимизацией затрат. Коммерческое предложение
AWADA - комфортное освещение с полным контролем и оптимизацией затрат. Коммерческое предложение ВКР: Монтаж силовых трансформаторов
ВКР: Монтаж силовых трансформаторов Презентация Гигиена и её назначение
Презентация Гигиена и её назначение Правила безопасного поведения на дороге (ПДД)
Правила безопасного поведения на дороге (ПДД) Изображение предметного мира - натюрморт
Изображение предметного мира - натюрморт Схемы. Виды схем
Схемы. Виды схем Адаптация ребенка в детском саду
Адаптация ребенка в детском саду Актуальность курса основы безопасности жизнедеятельности
Актуальность курса основы безопасности жизнедеятельности Вишивання бісером
Вишивання бісером Хімічна промисловість в Україні
Хімічна промисловість в Україні Понятие модели. Типы моделей
Понятие модели. Типы моделей Конструкція та міцність літальних апаратів. Системи протипожежного захисту
Конструкція та міцність літальних апаратів. Системи протипожежного захисту Правила поведения на дороге.
Правила поведения на дороге.