Содержание
- 2. Содержание Определение 3 Стандартная модель 4 Матричная модель 6 Арифметические действия 7 Геометрическая модель 9 Модуль
- 3. Определение Комплексные числа представляются в виде выражения: z = x + iy, где x, y –
- 4. Стандартная модель Комплексное число z можно определить как упорядоченную пару вещественных чисел; запись z = x
- 5. Стандартная модель Вещественные числа являются в этой модели подмножеством множества комплексных чисел и представлены парами вида
- 6. Матричная модель Комплексные числа можно также определить как: подкольцо кольца вещественных матриц 2×2 вида с обычным
- 7. Арифметические действия Сравнение x + iy = a + ib равны тогда и только тогда, когда
- 8. Арифметические действия Умножение (x + iy) ∙ (a + ib) = xa + xib + aiy
- 9. Геометрическая модель Любое комплексное число (кроме нуля) можно записать в тригонометрической форме: z = |z| ∙
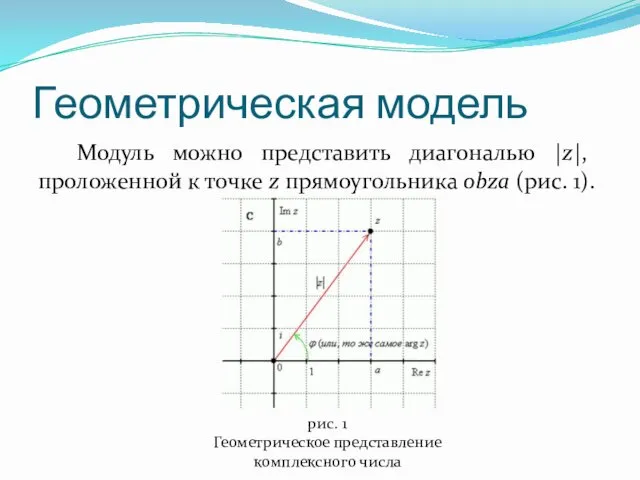
- 10. Геометрическая модель Модуль можно представить диагональю |z|, проложенной к точке z прямоугольника obza (рис. 1). рис.
- 11. Модуль и аргумент По теореме Пифагора легко вывести формулу для нахождения модуля комплексного числа: Угол φ
- 12. Модуль и аргумент Из этого определения следует, что: Если a = 0, то z является мнимым
- 13. Множество комплексных чисел с арифметическими действиями Множество всех комплексных чисел с арифметическими операциями является полем и
- 14. Сопряжённые числа Если комплексное число z = x + iy, то является сопряжённым к z. На
- 15. Сопряжённые числа Переход к сопряжённому числу можно рассматривать как одноместную операцию: Произведение и сумма комплексно-сопряженных чисел
- 16. Сопряжённые числа Умножение числителя и знаменателя комплексной дроби при комплексном знаменателе на сопряжённое к знаменателю выражению
- 17. Сопряжённые числа Рис. 2 Геометрическое представление сопряжённых чисел где r – модуль числа z, второе обозначение
- 18. Показательная форма Применяя к тригонометрической форме комплексного числа z = |z| ∙ (cosφ + i ·
- 19. Формула Муавра Формула Муавра помогает возводить в целую степень ненулевое комплексное число, представленное в тригонометрической форме.
- 20. Извлечение корней из комплексных чисел Аналогичная формула применима также и при вычислении корней n-ой степени из
- 22. Скачать презентацию


















 Презентация на классный час
Презентация на классный час Замки України
Замки України Презентация Каргопольская глиняная игрушка
Презентация Каргопольская глиняная игрушка Анализ языка и стиля текста СМИ
Анализ языка и стиля текста СМИ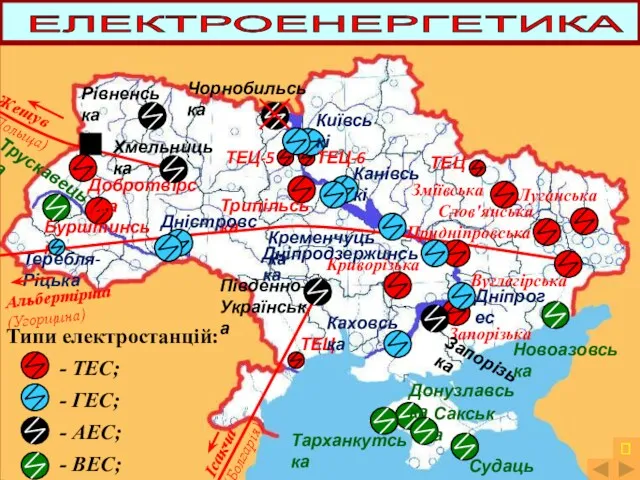 Металургiйний комплекс України
Металургiйний комплекс України Articles A/THE
Articles A/THE Фрезерный станок НГФ110Ш3 и технология фрезерования
Фрезерный станок НГФ110Ш3 и технология фрезерования Тест по химии (8 класс) по теме Генетическая связь классов неорганических соединений для системы тестирования PROClass
Тест по химии (8 класс) по теме Генетическая связь классов неорганических соединений для системы тестирования PROClass Штамповка. Технология горячей объемной штамповки
Штамповка. Технология горячей объемной штамповки Родина
Родина Обобщение темы Треугольник
Обобщение темы Треугольник Древнегреческий философ Аристотель
Древнегреческий философ Аристотель Философия Аристотеля. Онтология
Философия Аристотеля. Онтология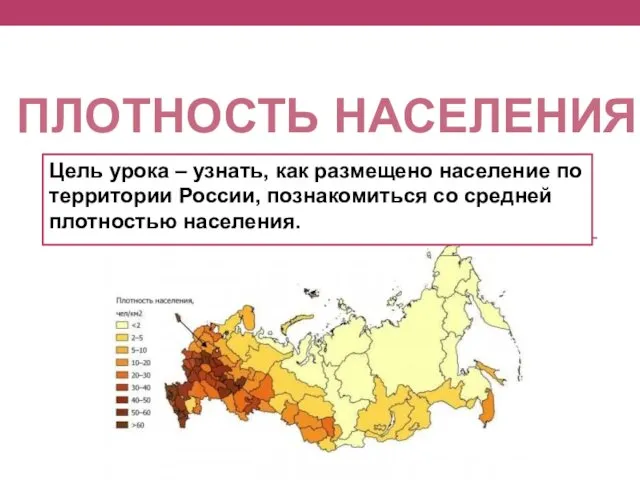 Размещение населения по территории России. Плотность населения
Размещение населения по территории России. Плотность населения Туберкулез. Первичное инфицирование
Туберкулез. Первичное инфицирование конкурс по экологии
конкурс по экологии Линейка моторных масел Лукойл Генезис
Линейка моторных масел Лукойл Генезис Основные параметры авиационных ГТД
Основные параметры авиационных ГТД Интерьер дома. Проект по технологии
Интерьер дома. Проект по технологии Основные модели развития науки о праве
Основные модели развития науки о праве Развивающие упражнения как средство повышения познавательной деятельности учащихся
Развивающие упражнения как средство повышения познавательной деятельности учащихся Чистохин Г.Д
Чистохин Г.Д Внутренняя политика в 1725-1762 гг
Внутренняя политика в 1725-1762 гг Профилактика эмоционального выгорания преподавателей и студентов
Профилактика эмоционального выгорания преподавателей и студентов Ваши возможности трудоустройства
Ваши возможности трудоустройства Снежинки
Снежинки Лекция 11. Классификация и возможности технических разведок
Лекция 11. Классификация и возможности технических разведок Отечественная война 1812 года в произведениях искусства
Отечественная война 1812 года в произведениях искусства