Содержание
- 2. Лекция № 1 §1. Комплексные числа и последовательности комплексных чисел. п. 1. Понятие комплексного числа. Геометрическая
- 3. Немного истории Комплексные числа вошли в математику в XVI в. как корни квадратного уравнения с отрицательным
- 4. Как понимать? Что делать?
- 5. Вначале такие корни отбрасывались, как «невозможные», «мнимые», и появление их считалось признаком отсутствия решения у задачи,
- 6. Обоснование: мнимые корни не выражают величины, так как их нельзя сравнивать друг с другом, нельзя сказать,
- 7. Однако позже было обнаружено, что над ними можно производить четыре алгебраических действия, причем сохраняются свойства, присущие
- 8. Это и послужило основанием называть мнимые корни числами («Алгебра» итальянского инженера Р. Бомбелли, 1572 г.).
- 9. Геометрическое изображение комплексных чисел в виде точек или векторов "на плоскости" было введено в 1799 г.
- 10. Символ i для мнимой единицы ввел в 1777 г. Л. Эйлер (1707— 1783). Термин «комплексное число»
- 11. Большое значение в раскрытии важной роли комплексных чисел в математике имели работы Л. Эйлера и К.
- 12. До появления этой теоремы можно было бы ожидать, что, подобно тому как квадратное уравнение привело к
- 13. Геометрическое изображение комплексного числа как точки или вектора на плоскости, естественно, приводит к мысли построить дальнейшие
- 14. Однако поиски числовой системы, зависящей от трех единиц: 1, i, j, геометрически изображаемой с помощью точек
- 15. В 1843 т. английский математик У. Гамильтон (1805—1865) показал, что можно построить числовые системы, зависящие от
- 16. Вообще, гиперкомплексными числами ранга п называются «числа» вида — единицы, —действительные числа, когда указаны правила алгебраических
- 17. Однако К. Вейерштрасс показал, что при п > 2 нельзя сохранить все свойства, присущие алгебраическим действиям
- 18. Немецкий математик Ф. Фробениус (1849—1917) доказал, что, даже отказавшись от переместительного закона умножения, можно сохранить остальные
- 19. -вектор Определим операцию сложения: операцию умножения на число: базис Рассмотрим плоскость R2.
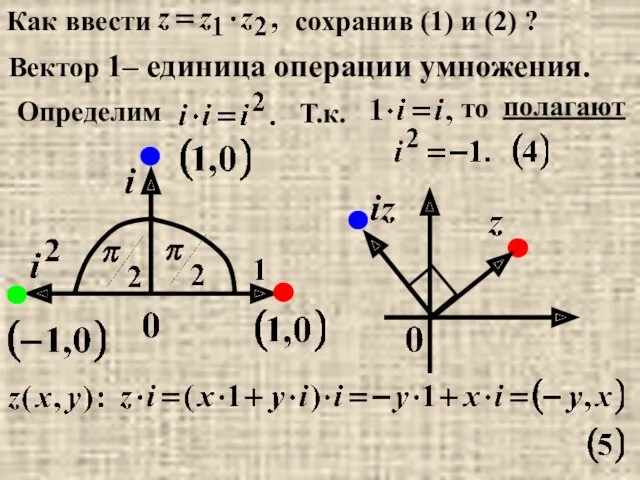
- 20. Как ввести сохранив (1) и (2) ? Вектор 1– единица операции умножения. Определим Т.к. то полагают
- 21. Правило умножения Def. Числовая плоскость называется комплексной плоскостью C, если для ее точек определены модули (1),
- 22. Действительные числа включаются в множество комплексных чисел. a=(a,0)-вещественное число, -1=(-1, 0), i =(0, 1)- мнимая единица,
- 23. Деление. Комплексное сопряжение.
- 24. Примеры.
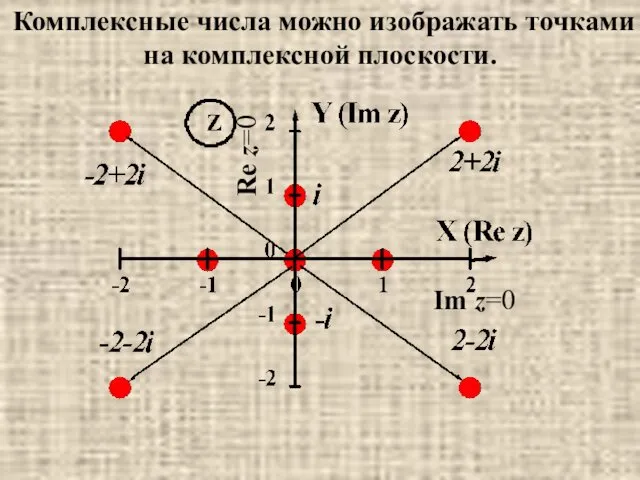
- 25. Комплексные числа можно изображать точками на комплексной плоскости. Im z=0 Re z=0
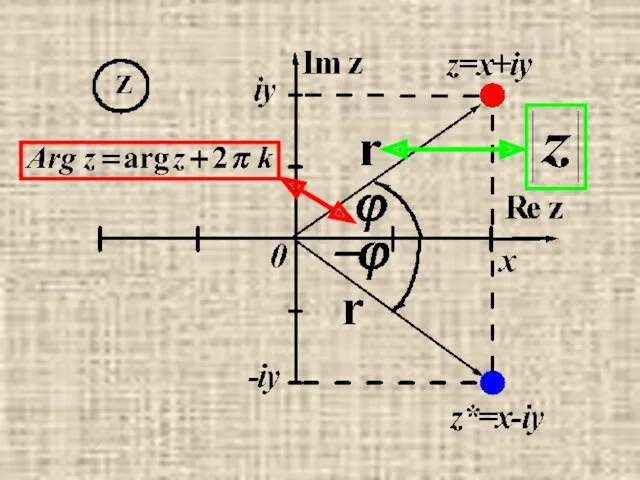
- 27. Модуль и аргумент комплексного числа Полярные координаты (x,y)↔(r,ϕ). Модуль комплексного числа: Аргумент комплексного числа: Главное значение
- 28. -разрез по - PC Soft -разрез по -литература Примеры. — не определен!
- 29. Тригонометрическая форма записи формула Эйлера: Показательная форма записи Теорема. Пусть тогда
- 30. Примеры.
- 31. Вопрос. Умножение и деление в показательной форме. Формула Муавра.
- 32. Извлечение корня. Корень n-той степени из комплексного числа принимает n различных значений.
- 33. Примеры.
- 37. Операция сравнения в С не определена. Множество комплексных чисел C образует поле. Поле С не является
- 38. Неравенства треугольника. Упорядоченная четверка является нормированным векторным пространством над полем R. Оно превратится в метрическое пространство,
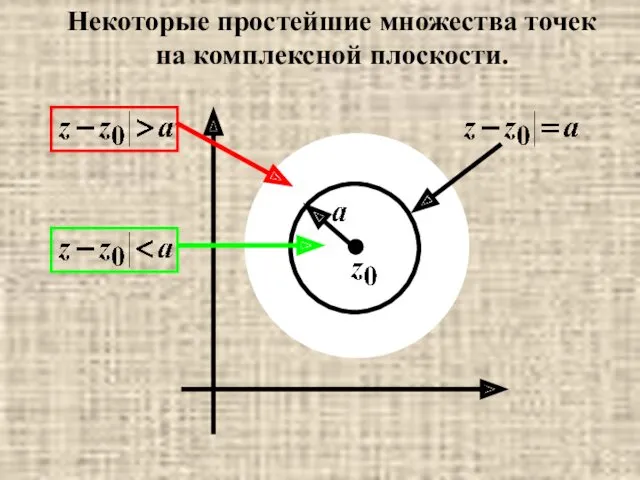
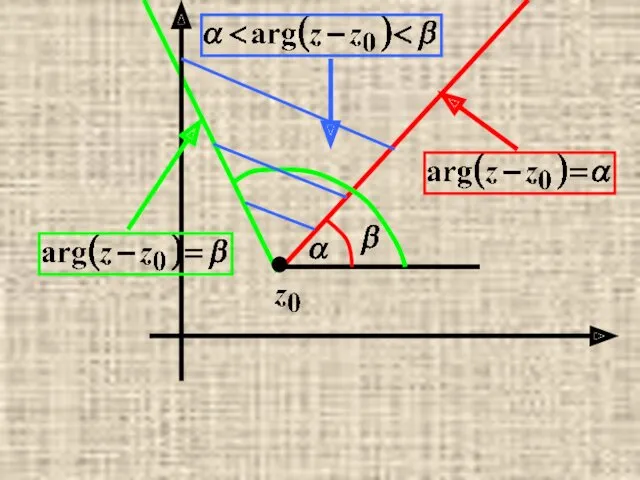
- 39. Некоторые простейшие множества точек на комплексной плоскости.
- 42. Скачать презентацию


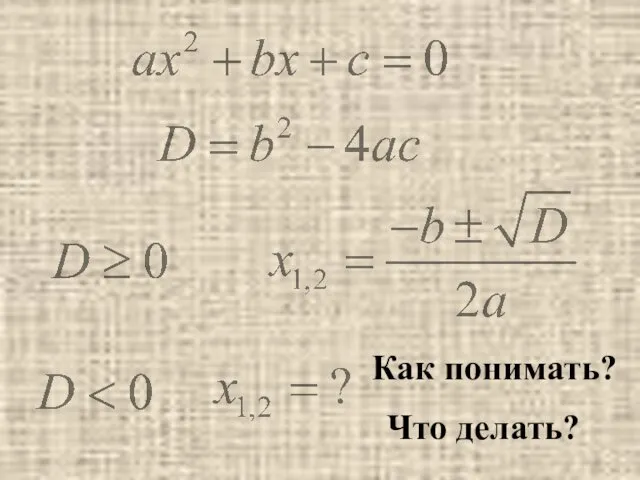






















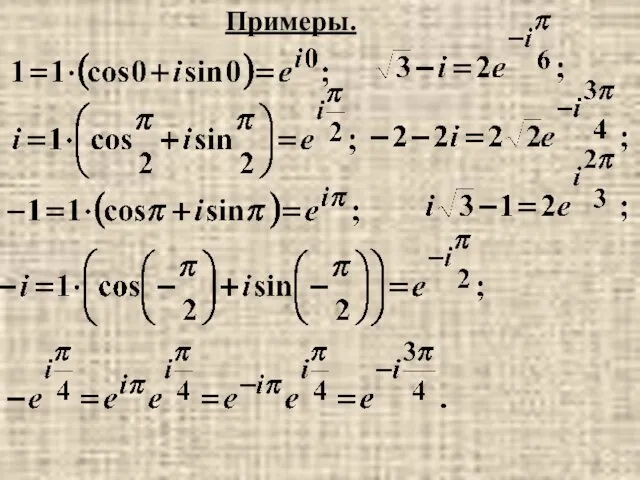



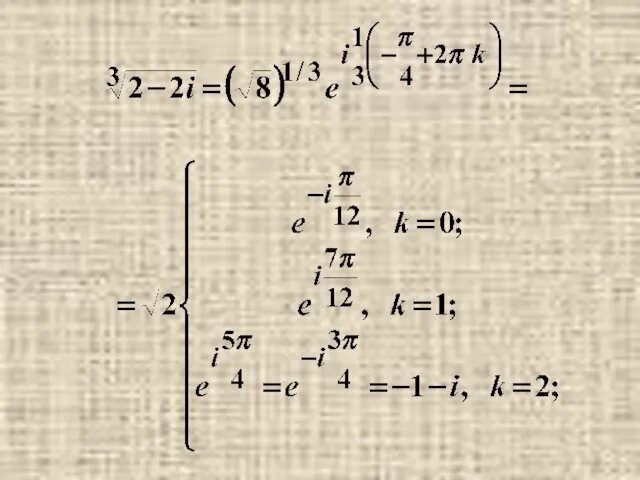
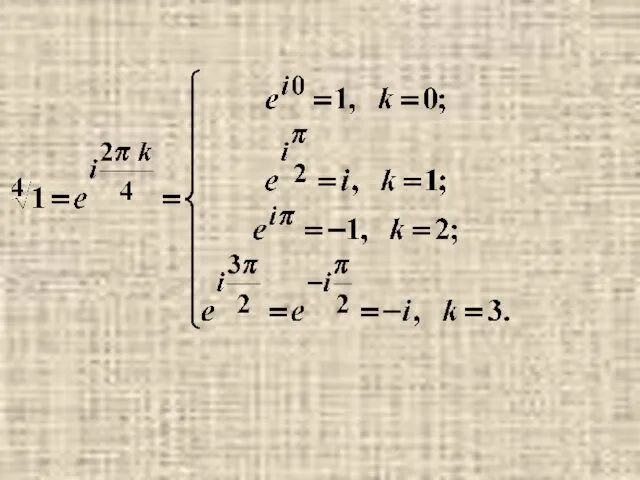
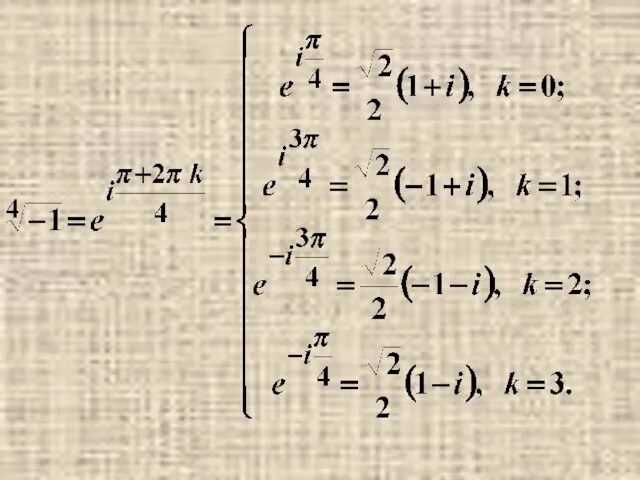


 Презентация Яблочный спас
Презентация Яблочный спас Холинергические средства
Холинергические средства Общее устройство автомобиля
Общее устройство автомобиля презентация Психологический климат семьи и семейный досуг как основа духовно-нравственного воспитания ребенка
презентация Психологический климат семьи и семейный досуг как основа духовно-нравственного воспитания ребенка Communication networks and switching systems
Communication networks and switching systems Процессор и оперативная память
Процессор и оперативная память Роль неблагоприятных факторов окружающей среды в развитии болезней органов дыхания у детей
Роль неблагоприятных факторов окружающей среды в развитии болезней органов дыхания у детей Дошкольное образование в Великобритании.
Дошкольное образование в Великобритании. Презентация к мастер-классу Методические приемы и формы реализации деятельностного подхода в обучении
Презентация к мастер-классу Методические приемы и формы реализации деятельностного подхода в обучении Пути снижения уровня издержек предприятия на примере ООО ГК Все люди равны
Пути снижения уровня издержек предприятия на примере ООО ГК Все люди равны Функции, строение, свойства, режимы и использование почв
Функции, строение, свойства, режимы и использование почв Элементы алгебры логики математические основы информатики
Элементы алгебры логики математические основы информатики Ссудный процент
Ссудный процент Особенности работы педагога-психолога с детьми с ранним детским аутизмом
Особенности работы педагога-психолога с детьми с ранним детским аутизмом Покорение космоса.
Покорение космоса. Нарушенные земли и общие подходы к их рекультивации
Нарушенные земли и общие подходы к их рекультивации Методы осмотра глазного дна
Методы осмотра глазного дна История малой родины – для всех поколений. Истории Зенгино
История малой родины – для всех поколений. Истории Зенгино Смутное время. Россия XVII век
Смутное время. Россия XVII век Дисперсионный анализ
Дисперсионный анализ Базовые эмоции
Базовые эмоции Афанасий Афанасьевич Фет 1820 - 1892
Афанасий Афанасьевич Фет 1820 - 1892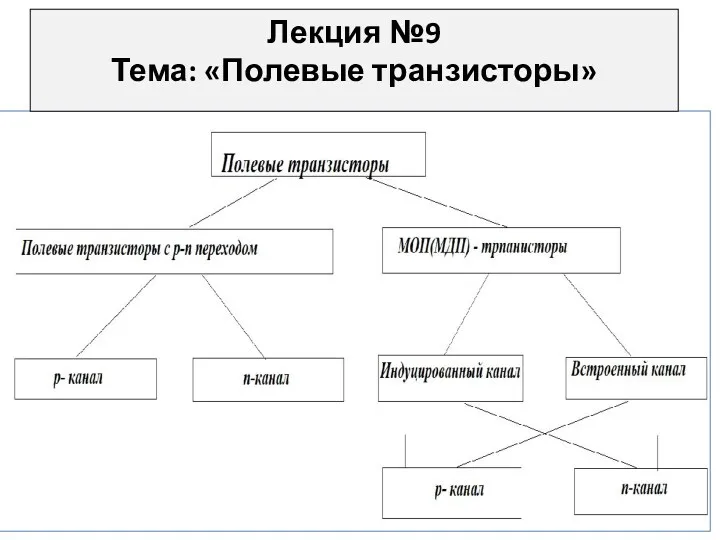 ЛК№9_Полевые транзистры p_n и МОП_ПВ
ЛК№9_Полевые транзистры p_n и МОП_ПВ Разработка урока технологии в 1 классе Елочка. УМК ПЕРСПЕКТИВНАЯ НАЧАЛЬНАЯ ШКОЛА
Разработка урока технологии в 1 классе Елочка. УМК ПЕРСПЕКТИВНАЯ НАЧАЛЬНАЯ ШКОЛА Понятие и сущность права
Понятие и сущность права Электролиттік диссоциация теориясы
Электролиттік диссоциация теориясы Хохлома. ИЗО
Хохлома. ИЗО Бульбоплоди (картопля, топінамбур)
Бульбоплоди (картопля, топінамбур)