Содержание
- 2. МАТЕМАТИЧЕСКОЕ МОДЕЛИРОВАНИЕ РАДИОТЕХНИЧЕСКИХ УСТРОЙСТВ И СИСТЕМ Тема 1. Методологические основы моделирования. Тема 2. Методы моделирования случайных
- 3. МОДЕЛИРОВАНИЕ – 1. Методологические основы моделирования замещение исследуемого объекта его условным образом, описанием или другим объектом,
- 4. МАТЕМАТИЧЕСКАЯ МОДЕЛЬ – 1. Методологические основы моделирования абстрактно-формализованное описание системы, например, в виде совокупности математических соотношений
- 5. КЛАССИФИКАЦИЯ МОДЕЛЕЙ 1. Методологические основы моделирования Структурные модели – отражают структуру системы, опираясь на ее устройство
- 6. ФОРМАЛЬНЫЕ КЛАССИФИКАЦИИ МАТЕМАТИЧЕСКИХ МОДЕЛЕЙ 1. Методологические основы моделирования Детерминированные / Стохастические Линейные / Нелинейные (по выполнению
- 7. АНАЛИТИЧЕСКОЕ МОДЕЛИРОВАНИЕ 1. Методологические основы моделирования процессы функционирования системы записываются в виде некоторых функциональных соотношений (алгебраических,
- 8. ИМИТАЦИОННОЕ МОДЕЛИРОВАНИЕ 1. Методологические основы моделирования воспроизводится алгоритм («логика») функционирования исследуемой системы во времени при различных
- 9. СТАТИСТИЧЕСКОЕ МОДЕЛИРОВАНИЕ 1. Методологические основы моделирования многократно повторяющееся имитационное моделирование работы стохастической системы с целью оценки
- 10. ПРИНЦИПЫ МОДЕЛИРОВАНИЯ 1. Методологические основы моделирования Принцип информационной достаточности – необходимо обладать достаточным объемом исходной информации
- 11. ЭТАПЫ МАТЕМАТИЧЕСКОГО МОДЕЛИРОВАНИЯ 1. Методологические основы моделирования Постановка задачи, определение объекта и целей исследования Выбор типа
- 12. ЭТАПЫ МОДЕЛИРОВАНИЯ НА ЭВМ 1. Методологические основы моделирования определение цели моделирования; 2) разработка концептуальной модели; 3)
- 13. ГЕНЕРАТОРЫ СЛУЧАЙНЫХ ЧИСЕЛ 2. Моделирование случайных величин. За эталон генератора случайных чисел (ГСЧ) принят такой генератор,
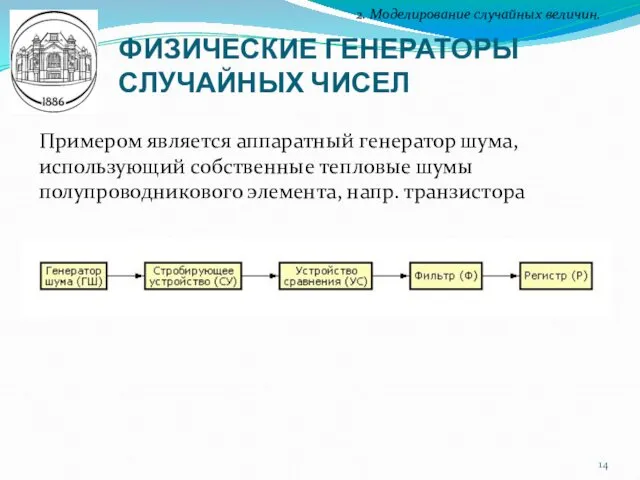
- 14. ФИЗИЧЕСКИЕ ГЕНЕРАТОРЫ СЛУЧАЙНЫХ ЧИСЕЛ 2. Моделирование случайных величин. Примером является аппаратный генератор шума, использующий собственные тепловые
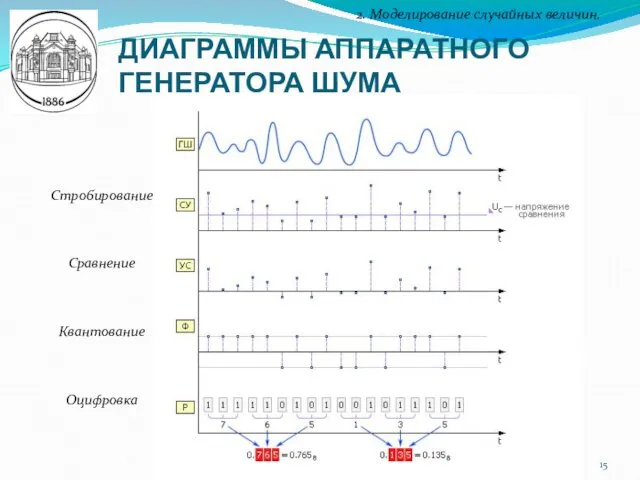
- 15. ДИАГРАММЫ АППАРАТНОГО ГЕНЕРАТОРА ШУМА 2. Моделирование случайных величин. Стробирование Сравнение Квантование Оцифровка
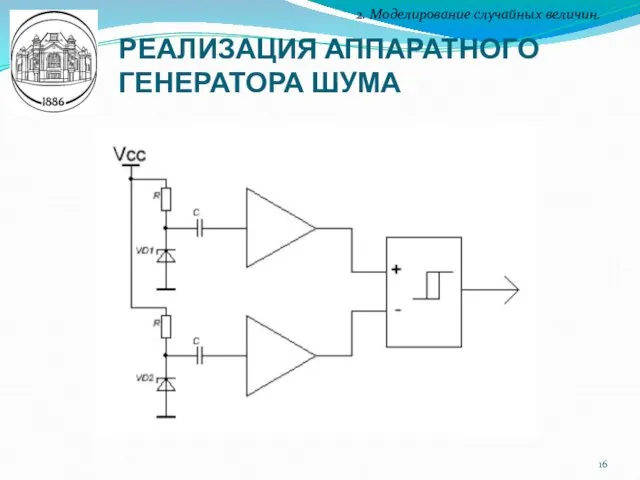
- 16. РЕАЛИЗАЦИЯ АППАРАТНОГО ГЕНЕРАТОРА ШУМА 2. Моделирование случайных величин.
- 17. АЛГОРИТМИЧЕСКИЕ ГЕНЕРАТОРЫ СЛУЧАЙНЫХ ЧИСЕЛ 2. Моделирование случайных величин. Метод серединных квадратов Недостатки: 1) если на некоторой
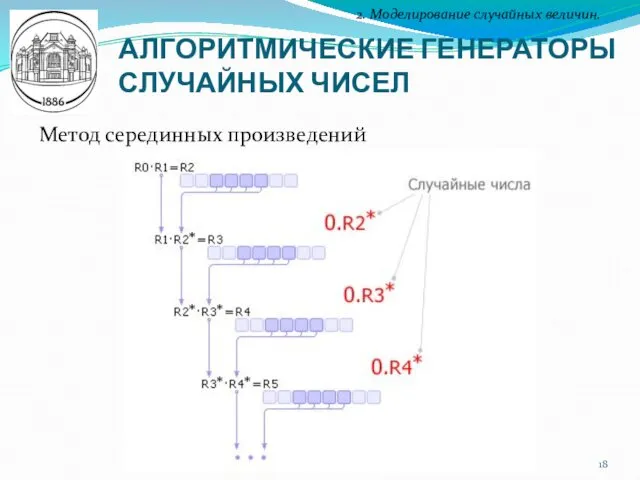
- 18. АЛГОРИТМИЧЕСКИЕ ГЕНЕРАТОРЫ СЛУЧАЙНЫХ ЧИСЕЛ 2. Моделирование случайных величин. Метод серединных произведений
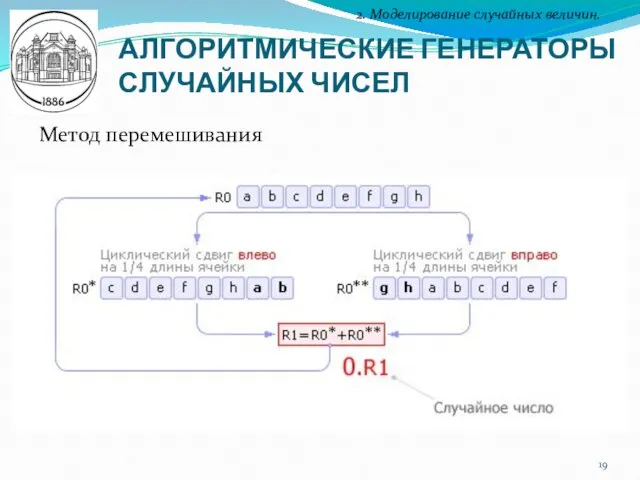
- 19. АЛГОРИТМИЧЕСКИЕ ГЕНЕРАТОРЫ СЛУЧАЙНЫХ ЧИСЕЛ 2. Моделирование случайных величин. Метод перемешивания
- 20. АЛГОРИТМИЧЕСКИЕ ГЕНЕРАТОРЫ СЛУЧАЙНЫХ ЧИСЕЛ 2. Моделирование случайных величин. Линейный конгруэнтный метод ri + 1 = mod(k
- 21. АЛГОРИТМИЧЕСКИЕ ГЕНЕРАТОРЫ СЛУЧАЙНЫХ ЧИСЕЛ 2. Моделирование случайных величин. Метод Фибоначчи с запаздываниями — вещественные числа из
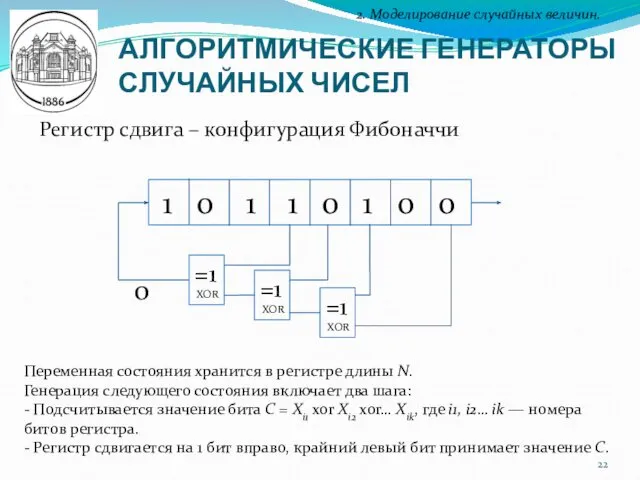
- 22. АЛГОРИТМИЧЕСКИЕ ГЕНЕРАТОРЫ СЛУЧАЙНЫХ ЧИСЕЛ 2. Моделирование случайных величин. Регистр сдвига – конфигурация Фибоначчи Переменная состояния хранится
- 23. АЛГОРИТМИЧЕСКИЕ ГЕНЕРАТОРЫ СЛУЧАЙНЫХ ЧИСЕЛ 2. Моделирование случайных величин. Регистр сдвига – конфигурация Галуа 1 0 1
- 24. АЛГОРИТМИЧЕСКИЕ ГЕНЕРАТОРЫ СЛУЧАЙНЫХ ЧИСЕЛ 2. Моделирование случайных величин. Обобщенный алгоритм генератора случайных чисел на регистре сдвига
- 25. АЛГОРИТМИЧЕСКИЕ ГЕНЕРАТОРЫ СЛУЧАЙНЫХ ЧИСЕЛ 2. Моделирование случайных величин. Обобщенный алгоритм генератора случайных чисел на регистре сдвига
- 26. ПРОВЕРКА КАЧЕСТВА РАБОТЫ ГЕНЕРАТОРА 2. Моделирование случайных величин. Проверки на равномерность распределения ГСЧ должен выдавать значения
- 27. ПРОВЕРКА КАЧЕСТВА РАБОТЫ ГЕНЕРАТОРА 2. Моделирование случайных величин. Проверки на равномерность распределения 2) Частотный тест –
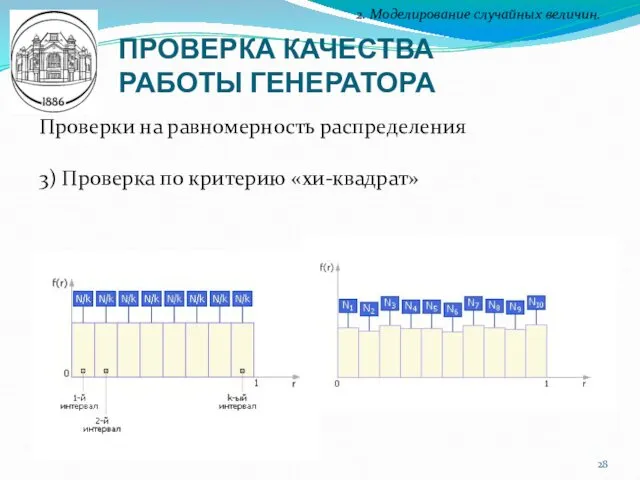
- 28. ПРОВЕРКА КАЧЕСТВА РАБОТЫ ГЕНЕРАТОРА 2. Моделирование случайных величин. Проверки на равномерность распределения 3) Проверка по критерию
- 29. ПРОВЕРКА КАЧЕСТВА РАБОТЫ ГЕНЕРАТОРА 2. Моделирование случайных величин. Проверки на равномерность распределения 3) Проверка по критерию
- 30. ПРОВЕРКА КАЧЕСТВА РАБОТЫ ГЕНЕРАТОРА 2. Моделирование случайных величин. Проверки на статистическую независимость Проверка на частоту появления
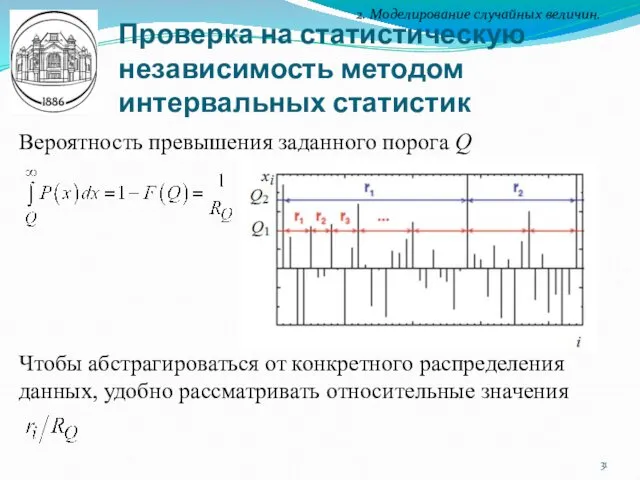
- 31. Вероятность превышения заданного порога Q Чтобы абстрагироваться от конкретного распределения данных, удобно рассматривать относительные значения Проверка
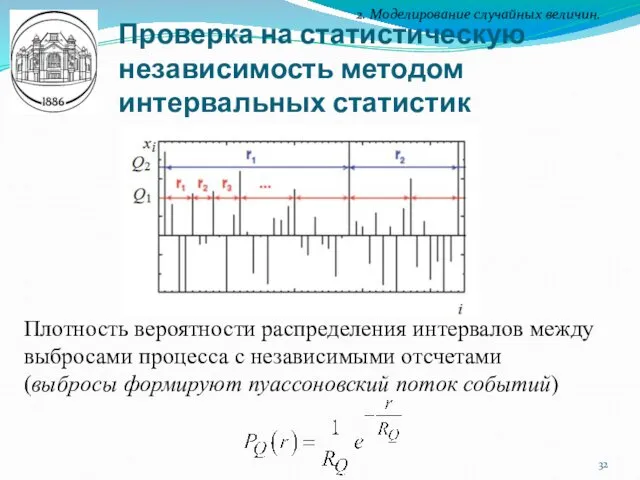
- 32. Проверка на статистическую независимость методом интервальных статистик 2. Моделирование случайных величин. Плотность вероятности распределения интервалов между
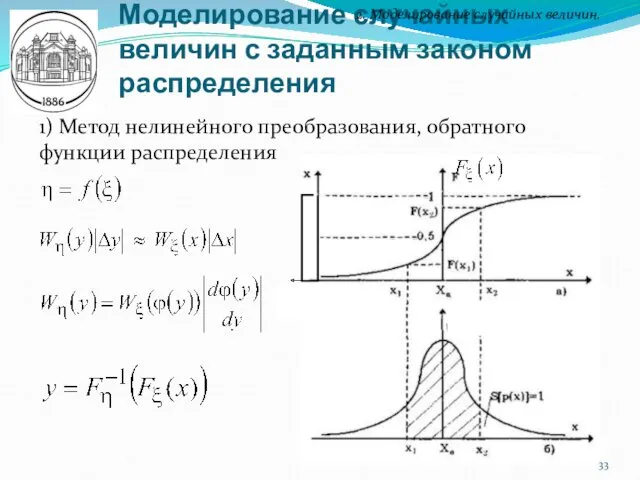
- 33. Моделирование случайных величин с заданным законом распределения 2. Моделирование случайных величин. 1) Метод нелинейного преобразования, обратного
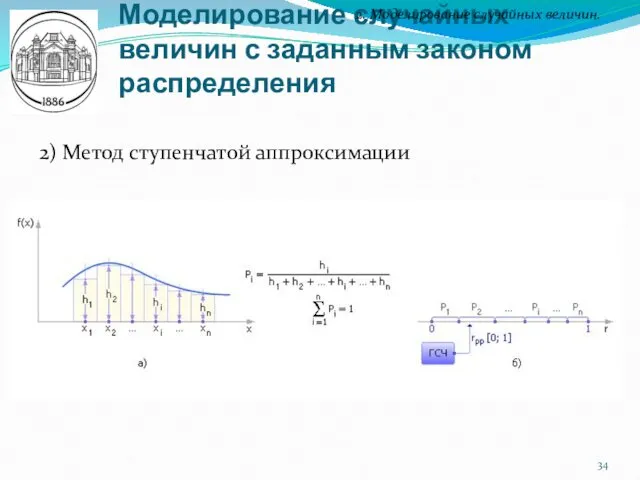
- 34. Моделирование случайных величин с заданным законом распределения 2. Моделирование случайных величин. 2) Метод ступенчатой аппроксимации
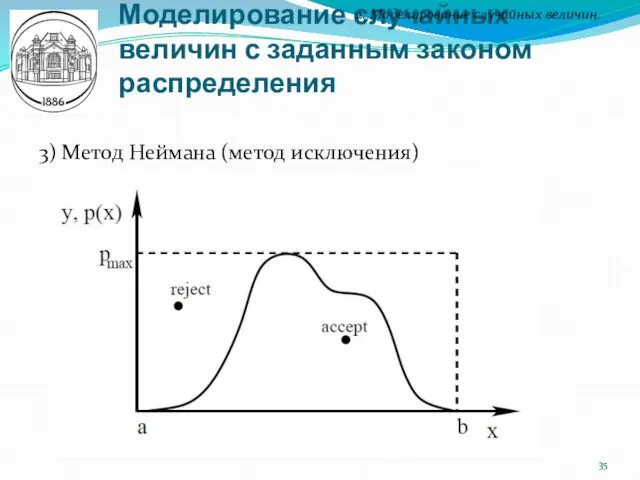
- 35. Моделирование случайных величин с заданным законом распределения 2. Моделирование случайных величин. 3) Метод Неймана (метод исключения)
- 36. Моделирование случайных величин с заданным законом распределения 2. Моделирование случайных величин. 4) Синтез нормального распределения из
- 37. Формирование случайных процессов с заданными корреляционными свойствами 2. Моделирование случайных процессов. Преобразование в линейной системе
- 38. За вычетом мат. ожидания АР1 имеет вид Модели случайных процессов с кратковременной зависимостью 2. Моделирование случайных
- 39. Модели случайных процессов с кратковременной зависимостью 2. Моделирование случайных процессов. Авторегрессионное уравнение 1-го порядка Дисперсия Условное
- 40. Модели случайных процессов с кратковременной зависимостью 2. Моделирование случайных процессов. Авторегрессионное уравнение 1-го порядка АКФ --
- 41. Модели случайных процессов с кратковременной зависимостью 2. Моделирование случайных процессов. Авторегрессионное уравнение 2-го порядка -- БШ
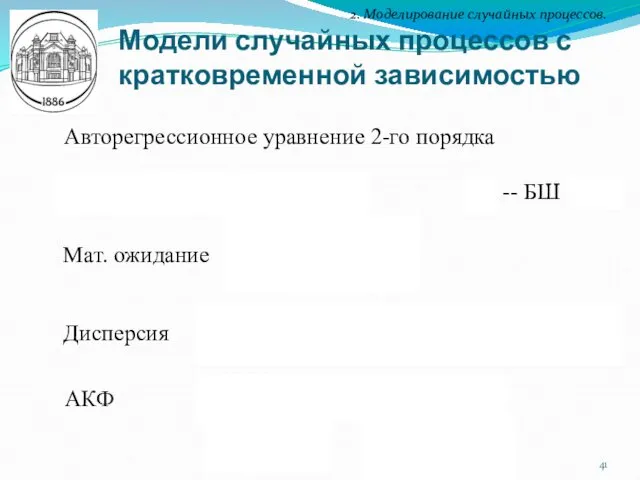
- 42. Модели случайных процессов с кратковременной зависимостью 2. Моделирование случайных процессов. Авторегрессионное уравнение p-го порядка -- БШ
- 43. Оценка параметров авторегрессионной модели данных 2. Моделирование случайных процессов. Уравнения Юла – Уокера В матричной форме
- 44. Оценка параметров авторегрессионной модели данных 2. Моделирование случайных процессов. Пример описания процесса АР-моделью по виду АКФ
- 45. Способы определения интервала корреляции 2. Моделирование случайных процессов. Определение 1 K Определение 2 K(τ) dτ Определения
- 46. Типовые АКФ и их интервалы корреляции 2. Моделирование случайных процессов.
- 47. Типовые АКФ и их интервалы корреляции 2. Моделирование случайных процессов.
- 48. Модели случайных процессов с кратковременной зависимостью 2. Моделирование случайных процессов. Модель скользящего среднего 1-го порядка Мат.
- 49. Модели случайных процессов с кратковременной зависимостью 2. Моделирование случайных процессов. Модель скользящего среднего 1-го порядка Ковариация
- 50. Модели случайных процессов с кратковременной зависимостью 2. Моделирование случайных процессов. Модель скользящего среднего q-го порядка Ковариация
- 51. Модели случайных процессов с кратковременной зависимостью 2. Моделирование случайных процессов. Модель авторегрессии – скользящего среднего 1-го
- 52. Модели случайных процессов с кратковременной зависимостью 2. Моделирование случайных процессов. Обобщенная модель авторегрессии – скользящего среднего
- 53. Модели интегрированных и долговременно-зависимых процессов 2. Моделирование случайных процессов. ARIMA – интегрированный ARMA (АРСС) Модель случайного
- 54. Модели интегрированных и долговременно-зависимых процессов 2. Моделирование случайных процессов. Модель случайного блуждания (Random Walk – RW)
- 55. Модели процессов с долговременной зависимостью (ДВЗ) 2. Моделирование случайных процессов. Процесс с бесконечным интервалом корреляции K(τ)
- 56. Самоподобные (масштабно—инвариантные) модели случайных процессов 2. Моделирование случайных процессов. При масштабировании имеем Показатель Хёрста Пример: задача
- 57. Модели случайных процессов со степенной АКФ (фрактальные модели) – частный случай СП с ДВЗ 2. Моделирование
- 58. Флуктуационный анализ 2. Моделирование случайных процессов. Введем функцию разбиения случайного процесса на v = N /
- 59. Флуктуационный анализ 2. Моделирование случайных процессов. Вычисление кумулятивной суммы Вычисление флуктуационной функции Вычисление отклонения от аппроксимации
- 60. Флуктуационный анализ на основе вейвлет-преобразования 2. Моделирование случайных процессов. Вычисление локальной суммы в сегменте k Взятие
- 61. Флуктуационный анализ на основе вейвлет-преобразования (WTA) 2. Моделирование случайных процессов.
- 62. Флуктуационный анализ методом центрированного скользящего среднего (CMA) 2. Моделирование случайных процессов. Вычисление кумулятивной суммы (профиля) Вычисление
- 63. Флуктуационный анализ методом центрированного скользящего среднего (CMA) 2. Моделирование случайных процессов.
- 64. Флуктуационный анализ с исключением полиномиального тренда (DFA) 2. Моделирование случайных процессов. Вычисление кумулятивной суммы Вычисление флуктуационной
- 65. Связь автокорреляционных и флуктуационных характеристик фрактального случайного процесса 2. Моделирование случайных процессов. Для процесса со степенной
- 66. Синтез и преобразования ДВЗ-процесса 2. Моделирование случайных процессов. Дифференцирование H = H – 1 Интегрирование H
- 67. Синтез ДВЗ-процесса методом линейной фильтрации 2. Моделирование случайных процессов.
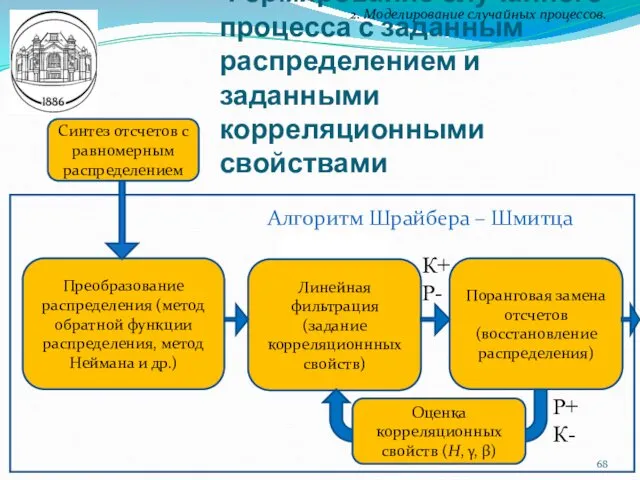
- 68. Формирование случайного процесса с заданным распределением и заданными корреляционными свойствами 2. Моделирование случайных процессов. Синтез отсчетов
- 69. Флуктуационный анализ с исключением полиномиального тренда (DFA) 2. Моделирование случайных процессов.
- 70. Флуктуационные функции 2. Моделирование случайных процессов.
- 71. 2. Моделирование случайных процессов. Сопоставление характеристик КВЗ- и ДВЗ-процессов (DFA)
- 72. 2. Моделирование случайных процессов. Сопоставление характеристик КВЗ- и ДВЗ-процессов (WTA)
- 73. 2. Моделирование случайных процессов. Сопоставление характеристик КВЗ- и ДВЗ-процессов (АКФ)
- 74. 2. Моделирование случайных процессов. Сопоставление характеристик КВЗ- и ДВЗ-процессов (СПМ)
- 75. 2. Моделирование случайных процессов. Моделирование процесса с нелинейной ДВЗ – биномиальный каскад
- 76. 2. Моделирование случайных процессов. Моделирование процесса с нелинейной ДВЗ – случайный мультипликативный каскад
- 77. 2. Моделирование случайных процессов. Каскады с фиксированными и случайными множителями Достоинство – легко получить аналитические решения
- 78. 2. Моделирование случайных процессов. Выбросы флуктуационных составляющих случайных процессов
- 79. 2. Моделирование случайных процессов. Статистики экстремумов вариационных рядов Экстремум вариационного ряда Вероятность появления хотя бы одного
- 80. 2. Моделирование случайных процессов. Обобщенные распределения экстремумов вариационных рядов Предельные распределения сводятся к трем основным случаям
- 81. 2. Моделирование случайных процессов. Интервальные статистики выбросов случайных процессов с линейной ДВЗ Плотность вероятности распределения интервалов
- 82. 2. Моделирование случайных процессов. Интервальные статистики выбросов случайных процессов с линейной ДВЗ Обобщенная аппроксимация ПВ растянутым
- 83. 2. Моделирование случайных процессов. Интервальные статистики выбросов случайных процессов с нелинейной ДВЗ При выраженной нелинейной зависимости
- 84. 2. Моделирование случайных процессов. Типичные виды ПВ интервалов для случайных процессов с ДВЗ
- 85. 2. Моделирование случайных процессов. Оценка вероятности выброса на основе интервальных статистик Оценка вероятности одно- или многократного
- 86. 2. Моделирование случайных процессов. Оценка вероятности выброса на основе интервальных статистик Для случайных процессов с линейной
- 87. 2. Моделирование случайных процессов. Оценка вероятности выброса на основе интервальных статистик Для случайных процессов с выраженной
- 88. 2. Моделирование случайных процессов. Оценка вероятности выброса на основе интервальных статистик Для случайных процессов с комбинированной
- 89. 2. Моделирование случайных процессов. Оценка вероятности выброса на основе интервальных статистик
- 91. Скачать презентацию








































































 Когда появилась одежда. (1 класс)
Когда появилась одежда. (1 класс) Регистры. Счетчики
Регистры. Счетчики Polymer Flooding for Enhanced Oil Recovery
Polymer Flooding for Enhanced Oil Recovery Автоматизация и механизация процессов листовой штамповки
Автоматизация и механизация процессов листовой штамповки Творческий проект по теме: Жанр романтической поэмы в творчестве М.Ю. Лермонтова
Творческий проект по теме: Жанр романтической поэмы в творчестве М.Ю. Лермонтова Аллергия. Аллергены
Аллергия. Аллергены Соединения на гвоздях
Соединения на гвоздях Зима в картинах русских художников
Зима в картинах русских художников Автоматизация производства. ИП Акулов Николай Николаевич
Автоматизация производства. ИП Акулов Николай Николаевич Атмосферные явления
Атмосферные явления Религиозные праздники России в XVI веке
Религиозные праздники России в XVI веке Комплаентность пациента с артериальной гипертензией. Роль фельдшера
Комплаентность пациента с артериальной гипертензией. Роль фельдшера Автоматизированные системы для мониторинга газовых выбросов из фиксированных источников
Автоматизированные системы для мониторинга газовых выбросов из фиксированных источников Біблійна антропологія. Вчення про людину – розділ систематичної теології
Біблійна антропологія. Вчення про людину – розділ систематичної теології Залізничний транспорт
Залізничний транспорт Приоритеты в организации и содержании управления на основе выявленных проблем системы образования города Новосибирска
Приоритеты в организации и содержании управления на основе выявленных проблем системы образования города Новосибирска Повторение: подготовка к ГИА по математике: алгебра, геометрия, теория вероятностей (8, 9 класс) Диск Диск Диск Диск
Повторение: подготовка к ГИА по математике: алгебра, геометрия, теория вероятностей (8, 9 класс) Диск Диск Диск Диск Принцесса Грёз или Женщина - Гражданка О чем писали женские журналы в 1917 году
Принцесса Грёз или Женщина - Гражданка О чем писали женские журналы в 1917 году урок с презентацией химия 9класс Предмет органической химии
урок с презентацией химия 9класс Предмет органической химии Презентация Игрушки из скрученных полосок
Презентация Игрушки из скрученных полосок Возбуждение и рассмотрение дела об административном правонарушении
Возбуждение и рассмотрение дела об административном правонарушении Коммутация и программирование щитов
Коммутация и программирование щитов Понятие о методах обучения и их классификация
Понятие о методах обучения и их классификация Сети. Интернет. Протоколы
Сети. Интернет. Протоколы Шоколадное печенье в виде футбольного мяча
Шоколадное печенье в виде футбольного мяча Итоги обучения в 3 классе!
Итоги обучения в 3 классе! Ішекті өңдеу. Ішек компектісі туралы түсінік. (Дәріс 11-12)
Ішекті өңдеу. Ішек компектісі туралы түсінік. (Дәріс 11-12) Умножение многочленов. Формулы сокращенного умножения
Умножение многочленов. Формулы сокращенного умножения