Содержание
- 2. Введение Математика — фундаментальная наука, предоставляющая (общие) языковые средства другим наукам; тем самым она выявляет их
- 3. Элементы теории матриц
- 4. Сумма (разность) двух матриц и одинакового размера определяется следующим образом: Для умножения матрицы на число нужно
- 5. Произведением матрицы A из m строк и k столбцов на матрицу B из k строк и
- 6. Пример. В частности,
- 7. Правило Крамера и определители матриц 2-го и 3-го порядков Рассмотрим матрицу второго порядка: Число называется определителем
- 8. Определитель третьего порядка обозначается и вычисляется по формуле
- 9. Решение системы трех уравнений с тремя неизвестными выражается через определители третьего порядка по фор-мулам Крамера:
- 10. Вектор – это направленный отрезок. Обозначается вектор символом или , где точка А – начало, а
- 11. Линейные операции над векторами Произведением вектора на число к называется вектор , который: имеет длину коллинеарен
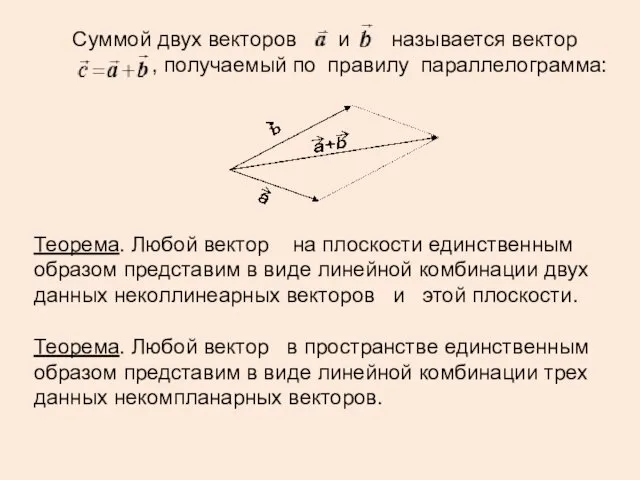
- 12. Суммой двух векторов и называется вектор , получаемый по правилу параллелограмма: Теорема. Любой вектор на плоскости
- 13. Базисом называются взятые в определенном порядке линейно независимые векторы. Если базисные векторы взаимно перпендикулярны, то базис
- 14. Декартовой прямоугольной системой координат называется совокупность фиксированной точки О (начала координат) и базиса векторов , исходящих
- 15. Радиус-вектором произвольной точки М называют вектор , а его координаты называют координатами этой точки. Для произвольной
- 16. Скалярное произведение Скалярным произведением векторов называется число, равное произведению длин этих векторов на косинус угла между
- 17. С помощью скалярного произведения можно вычислить угол между векторами: В частности, условие ортогональности двух векторов выражается
- 18. Прямая линия на плоскости Общее уравнение прямой – уравнение прямой L, проходящей через заданную точку перпендикулярно
- 19. Уравнение прямой с угловым коэффициентом прямая L пересекает ось ординат в точке (0, b) и образует
- 20. Уравнение прямой, проходящей через две заданные точки Положительный угол φ, который отсчитывается от прямой до прямой
- 21. Пример 1. Составить общее уравнение прямой на плоскости, если она проходит через точку и вектор нормали
- 22. Пример 2. Найти угол между прямыми, заданными общими уравнениями и . Решение. Используя формулу, получаем: Получаем
- 23. Пример 3. Написать уравнение прямой, которая проходит через две заданные точки (-1, 2) и (2, 1).
- 24. Элементы математического анализа Пусть заданы два множества X и Y произвольной природы. Допустим, что каждому элементу
- 25. Предел функции — одно из основных понятий математического анализа. Функция f(x) имеет предел A в точке
- 27. Дифференцирование Производная (функции в точке) — основное понятие дифференциального исчисления, характеризующее скорость изменения функции (в данной
- 28. Вычисление производных Правила дифференцирования: Производная суммы конечного числа дифференцируемых функций равна сумме производных этих функций Производная
- 29. Постоянный множитель при дифференцировании выносится за знак производной Производная частного вычисляется по следующей формуле
- 30. Таблица основных производных
- 31. Производная сложной функции по независимой переменной равна произведению производной функции по промежуточной переменной на производную промежуточной
- 33. Пример. Найти экстремумы функции Функция определена на всей числовой прямой. Её производная всюду существует, поэтому абсциссы
- 34. Интегрирование Функция F(x) называется первообразной для функции f(x) на интервале X=(a, b) (конечном или бесконечном), если
- 35. Правила интегрирования
- 36. Таблица интегралов
- 37. Пример. Найти интеграл Решение. Согласно тождеству , получим
- 38. Интегрирование методами подстановки и замены переменной. Формула подстановки Пример. Вычислить Решение. Делая в этой формуле подстановку
- 40. Формула интегрирования по частям Пример. Вычислить Решение. Введем обозначения: , Тогда , Применяя формулу интегрирования по
- 41. Определённым интегралом функции на промежутке называется конечный предел интегральных сумм если он существует и не зависит
- 42. Формула Ньютона – Лейбница вычисления определенного интеграла: Формула интегрирования по частям:
- 43. Пример. Найти площадь фигуры, ограниченной линией осью абсцисс и прямой . Искомая площадь (см. рис.) выражается
- 44. Правило замены переменной в определённом интеграле. Пусть требуется вычислить интеграл . Заменим , причем концам промежутка
- 45. Пример. Вычислить определенный интеграл Решение. Произведём замену переменной, полагая Тогда dt = 2x dx, откуда x
- 46. Основные понятия теории дифференциальных уравнений Дифференциальным уравнением называется уравнение, связывающее независимую переменную, неизвестную функцию и ее
- 47. Уравнения первого порядка Общий вид дифференциального уравнения первого порядка: Пример. Пусть имеется уравнение Непосредственной подстановкой убеждаемся
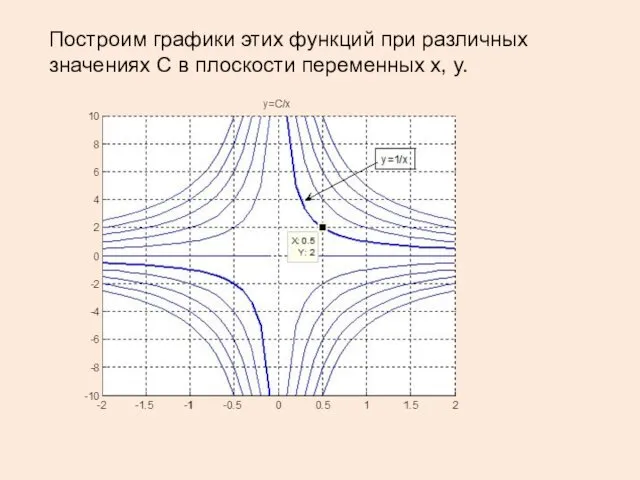
- 48. Построим графики этих функций при различных значениях C в плоскости переменных x, y.
- 49. Формула (*) определяет общее решение уравнения, представляющее собой семейство кривых. Выберем точку с координатами (на рис.
- 50. Для произвольного дифференциального уравнения первого порядка общее решение имеет вид функции содержащей параметр С. Графики функций
- 51. Уравнения с разделяющимися переменными Если в дифференциальном уравнении правая часть может быть представлена в виде произведения
- 52. Пример. Решить дифференциальное уравнение Решение. Так как , то . Далее разделяем переменные: Следующий этап –
- 55. Линейные однородные дифференциальные уравнения второго порядка с постоянными коэффициентами Общий вид: (**) Характеристическое уравнение: (**)
- 56. Если уравнение (*) имеет два различных действительных корня и , то общее решение уравнения (**) имеет
- 57. Пример 1. Решить уравнение y`` + 3y` + 2y = 0. Решение. Данное уравнение является линейным
- 60. Скачать презентацию
































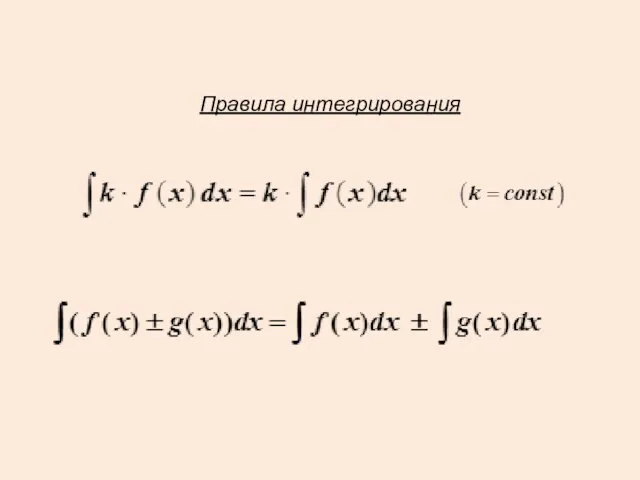






















 Презентация Пуговка на счастье
Презентация Пуговка на счастье Изготовление заготовок ковкой
Изготовление заготовок ковкой материал для фестиваля народов мира. Русский народ
материал для фестиваля народов мира. Русский народ Дорожный контроллер ЕС-2. Эксплуатация
Дорожный контроллер ЕС-2. Эксплуатация Биосоциальная сущность личности (задания ОГЭ)
Биосоциальная сущность личности (задания ОГЭ) День православной книги
День православной книги Снаряжение для пешеходного туризма. (Тема 2)
Снаряжение для пешеходного туризма. (Тема 2) Денежные реформы России
Денежные реформы России Какую форму имеет Земля?
Какую форму имеет Земля?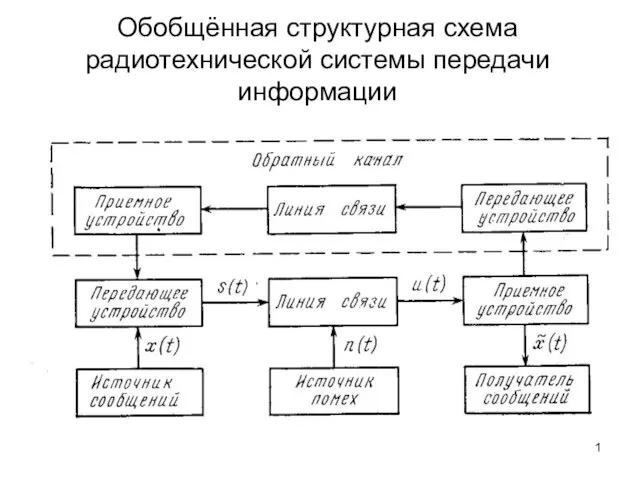 Обобщённая структурная схема радиотехнической системы передачи информации
Обобщённая структурная схема радиотехнической системы передачи информации Вторая Мировая война
Вторая Мировая война Экоурок Свобода от отходов
Экоурок Свобода от отходов Провешивание поверхностей
Провешивание поверхностей Зона транспортной инфраструктуры
Зона транспортной инфраструктуры Звуки и буквы Ч-Ть
Звуки и буквы Ч-Ть Очистка газов от пыли. Характеристики аппаратов для очистки аэрозолей
Очистка газов от пыли. Характеристики аппаратов для очистки аэрозолей Измерения параметров в процессе строительства ВОЛС. Приемо-сдаточные испытания
Измерения параметров в процессе строительства ВОЛС. Приемо-сдаточные испытания Творческая работа учащихся Выращивание кристаллов
Творческая работа учащихся Выращивание кристаллов МАС 5G. Концепции построения и развития Единой сети связи России
МАС 5G. Концепции построения и развития Единой сети связи России Оформление участка в зимнее время года
Оформление участка в зимнее время года Прикладное ПО. Инструментальное ПО
Прикладное ПО. Инструментальное ПО Профилактика психоэмоционального выгорания педагогов
Профилактика психоэмоционального выгорания педагогов Рациональное питание
Рациональное питание Иммунопатологиялық үрдістер
Иммунопатологиялық үрдістер Производство вафель
Производство вафель Разноцветные жуки. 1 класс
Разноцветные жуки. 1 класс Трикотажное полотно. Строение и свойства трикотажного полотна. Классификация трикотажных переплетений
Трикотажное полотно. Строение и свойства трикотажного полотна. Классификация трикотажных переплетений Из жизни слов. Слова добро и зло
Из жизни слов. Слова добро и зло