Содержание
- 2. Определение: Матрица – прямоугольная таблица, образованная из элементов некоторого множества и состоящая из m строк и
- 3. Среди квадратных матриц выделяют класс диагональных матриц, т.е. матрицы, которые имеют элементы не равные нулю только
- 4. Матрица, у которой все элементы нулевые, получила название нулевой: Понятие нулевой матрицы можно вводить и для
- 5. Основные операции, которые производятся над матрицами: 1. Сложение матриц. 2. Вычитание матриц. 3. Умножение матрицы на
- 6. 1. Суммой двух матриц А и В, одинаковых размерностей, называется матрица той же размерности, элементы которой
- 7. Сумма матриц обладает следующими свойствами: А+В=В+А, сложение матриц коммутативно, А+(В+С)=(А+В)+С, свойство ассоциативности, А+0=А, где 0 –
- 8. 3. Произведением матрицы А на число λ, называется матрица, элементы которой получаются из соответствующих элементов матрицы
- 9. 4. Произведение АВ матрицы А на матрицу В определяется только в том случае, когда число столбцов
- 10. В таком случае произведением матрицы A на матрицу B является матрица С элементы которой определяются по
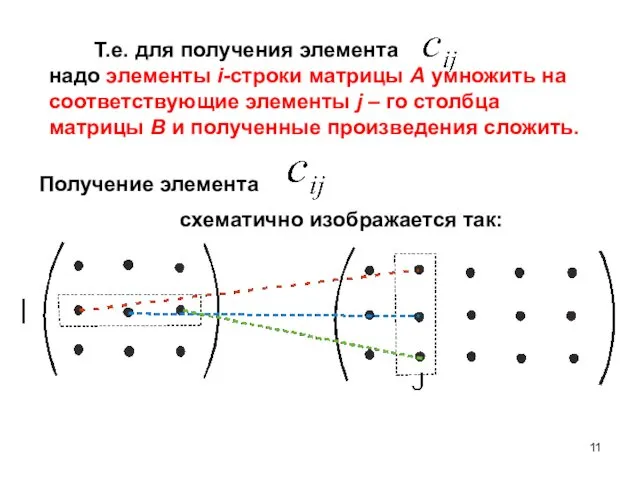
- 11. Т.е. для получения элемента надо элементы i-строки матрицы А умножить на соответствующие элементы j – го
- 12. Пример: Перемножить матрицы и Решение:
- 13. Свойства умножений матриц: произведение матриц не коммутативно; Если AB=BA, то матрицы А и В называются перестановочными;
- 14. свойство ассоциативности свойство дистрибутивности Непосредственной проверкой можно убедиться, что
- 15. 2.2 Обратная матрица. Пусть дана квадратная матрица: и определитель матрицы. Матрица определитель которой равен нулю, называется
- 16. Если для данной матрицы А существует матрица Х, такая, что где Е – единичная матрица, то
- 17. Пусть для матрицы А существует обратная матрица Х, тогда должно выполняться условие (2.6) Пусть для матрицы
- 18. Запишем выражение для обратной матрицы Пусть дана квадратная обратимая матрица А: Найдём алгебраические дополнения для каждого
- 19. Обратную матрицу можно найти по формуле
- 20. Пример: Найти матрицу обратную данной Решение: Проверим, обратима матрица А или нет, т.е. является ли она
- 22. Запишем обратную матрицу Для проверки правильности решения достаточно проверить следующее равенство:
- 23. 2.3 Ранг матрицы. Рассмотрим произвольную прямоугольную матрицу: Возьмем в этой матрицы k строк и k столбцов.
- 24. Если любой минор а все возможные миноры равны нулю, то говорят, что ранг матрицы равен k
- 25. Пример: Вычислить ранг матрицы: Решение: Выберем минор второго порядка, находящийся в верхнем левом углу, Минор второго
- 27. Другим простым способом вычисления ранга матрицы является метод Гаусса, основанный на элементарных преобразованиях, выполняемых над матрицей.
- 28. Метод Гаусса вычисления ранга матрицы заключается в том, что при помощи элементарных преобразований матрицу можно привести
- 29. Пример: Найти ранг матрицы: Решение: Добьемся, чтобы все элементы первого столбца, кроме первого были нулями. Первую
- 31. Скачать презентацию


















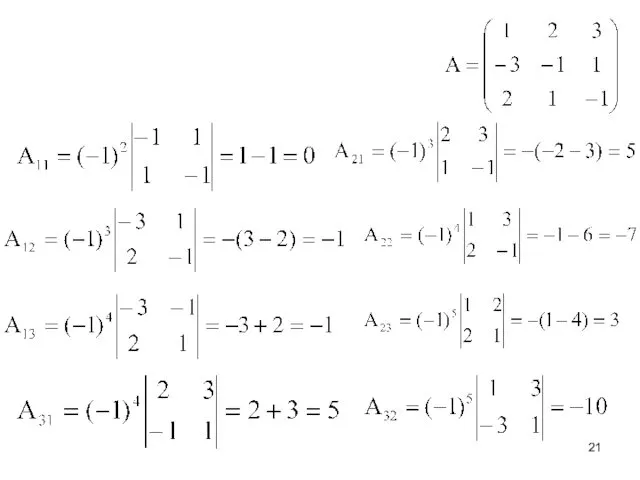








 Основы производства комбикормов
Основы производства комбикормов Регулирование частоты вращения асинхронных двигателей с фазным ротором
Регулирование частоты вращения асинхронных двигателей с фазным ротором Что такое технология
Что такое технология Силовая электроника. Лекция 1
Силовая электроника. Лекция 1 Городской транспорт
Городской транспорт Правописание [не] с глаголами
Правописание [не] с глаголами Презентация к уроку по теме Дробные выражения
Презентация к уроку по теме Дробные выражения Внеклассное мероприятие Игра: ЧТО? ГДЕ? КОГДА?
Внеклассное мероприятие Игра: ЧТО? ГДЕ? КОГДА? Оказание государственной поддержки малым формам хозяйствования в Удмуртской Республике
Оказание государственной поддержки малым формам хозяйствования в Удмуртской Республике Взаимное расположение двух окружностей
Взаимное расположение двух окружностей Библейские притчи
Библейские притчи Горнодобывающая отрасль
Горнодобывающая отрасль Педсовет: Использование новых активных форм и методов обучения в учебно-воспитательном процессе
Педсовет: Использование новых активных форм и методов обучения в учебно-воспитательном процессе Игра - пособие Русская матрешка
Игра - пособие Русская матрешка Обоснование экономической эффективности инвестиционного проекта ООО Вернисаж
Обоснование экономической эффективности инвестиционного проекта ООО Вернисаж Правильные и неправильные дроби
Правильные и неправильные дроби Бактерии
Бактерии Каталог характеристик лопастных насосов
Каталог характеристик лопастных насосов Генетика популяций
Генетика популяций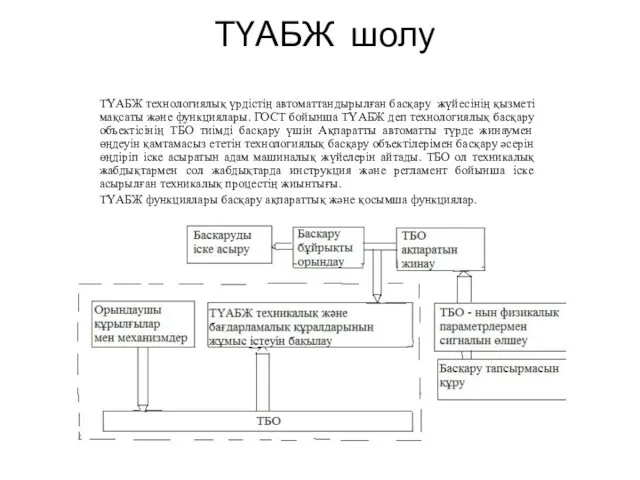 ТҮАБЖ шолу
ТҮАБЖ шолу Милосердие, забота о слабых, взаимопомощь, социальные проблемы общества и отношение к ним разных религий
Милосердие, забота о слабых, взаимопомощь, социальные проблемы общества и отношение к ним разных религий Вступление в систему непрерывного медицинского и фармацевтического образования. Пошаговые инструкции
Вступление в систему непрерывного медицинского и фармацевтического образования. Пошаговые инструкции Принципы организации развивающей предметно-пространственной среды в группах детского сада в соответствии с Федеральным государственным образовательным стандартом дошкольных организаций.
Принципы организации развивающей предметно-пространственной среды в группах детского сада в соответствии с Федеральным государственным образовательным стандартом дошкольных организаций. Профилактика суицидальных тенденций среди несовершеннолетних в условиях урочной и внеурочной деятельности
Профилактика суицидальных тенденций среди несовершеннолетних в условиях урочной и внеурочной деятельности Алканы, алкены, алкины
Алканы, алкены, алкины Презентация Золотые рыбки в технике оригами
Презентация Золотые рыбки в технике оригами Строительная теплотехника
Строительная теплотехника Изучение факторов, способствующих лучшей взбитости мороженого
Изучение факторов, способствующих лучшей взбитости мороженого