Содержание
- 2. МАТРИЦЫ И ДЕЙСТВИЯ НАД НИМИ Матрицей размера m x n называется прямоугольная таблица чисел, содержащая m
- 3. Обозначение: где i=1,2…m j=1,2…n - матрица размерности m x n - элемент матрицы i –ой строки
- 4. матрица размерности m x n
- 5. Две матрицы называются равными, если у них одинаковая размерность и совпадают строки и столбцы. Если число
- 6. Пример: - квадратная матрица размерности 3х3
- 7. Элементы матрицы aij , у которых номер столбца совпадает с номером строки, называются диагональными. Если в
- 8. единичная матрица
- 9. Матрица любого размера называется нулевой, если все ее элементы равны 0. нулевая матрица
- 10. Матрица, состоящая из одной строки, называется матрицей-строкой или вектором-строкой. матрица-строка
- 11. Матрица, состоящая из одного столбца, называется матрицей-столбцом или вектором-столбцом. матрица-столбец
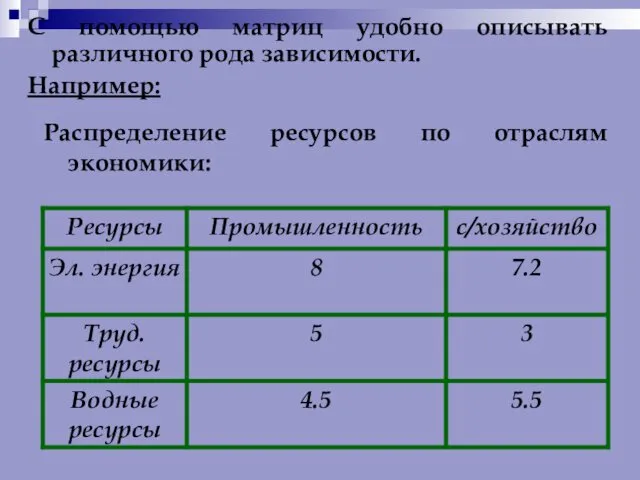
- 12. Распределение ресурсов по отраслям экономики: С помощью матриц удобно описывать различного рода зависимости. Например:
- 13. Эту зависимость можно представить в виде матрицы: Где элемент aij показывает сколько i – го ресурса
- 14. ДЕЙСТВИЯ НАД МАТРИЦАМИ 1. Умножение матрицы на число Чтобы умножить матрицу на число, надо каждый элемент
- 15. Пусть дана матрица Умножаем ее на число λ: Где каждый элемент матрицы В: Где:
- 16. Например: Умножая матрицу на число 2, получим:
- 17. 2. Сложение матриц Складываются матрицы одинаковой размерности. Получается матрица той же размерности, каждый элемент которой равен
- 18. Пусть даны матрицы Складываем их: Где каждый элемент матрицы С: Аналогично проводится вычитание матриц.
- 19. Пример. Найти сумму и разность матриц:
- 20. Решение:
- 21. 3. Умножение матриц Умножение матриц возможно, если число столбцов первой матрицы равно числу строк второй. Тогда
- 22. Пусть даны матрицы Умножаем их: Где каждый элемент матрицы С:
- 23. Пример. Найти произведение матриц:
- 24. Число столбцов первой матрицы равно числу строк второй, следовательно их произведение существует: Решение:
- 25. Теперь перемножим матрицы в обратном порядке: Умножение матриц в общем случае некоммутативно:
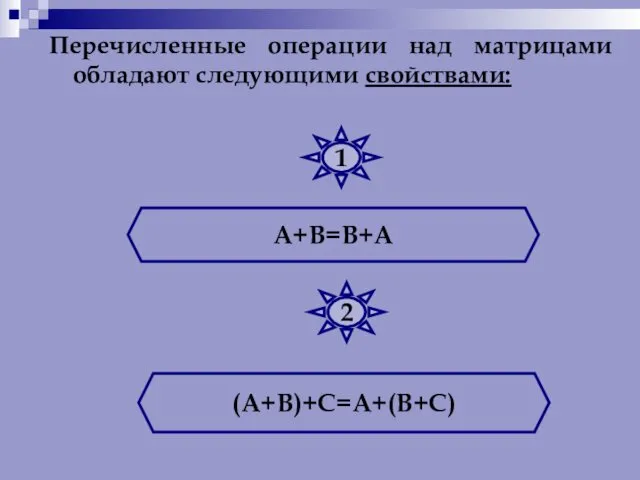
- 26. Перечисленные операции над матрицами обладают следующими свойствами: А+В=В+А (А+В)+С=А+(В+С) 1 2
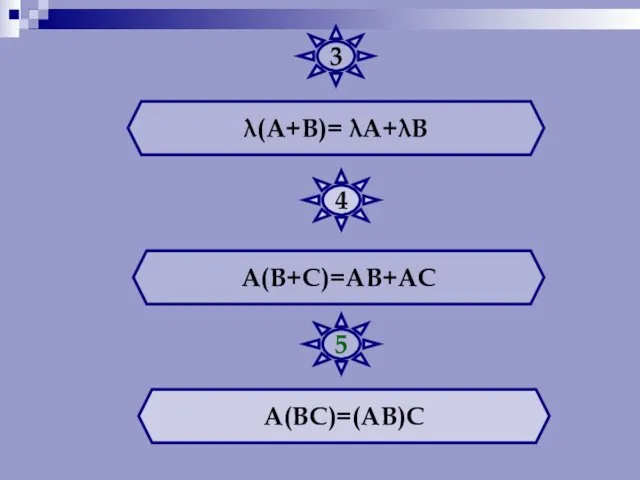
- 27. λ(А+В)= λА+λВ А(В+С)=АВ+АС А(ВС)=(АВ)С 3 4 5
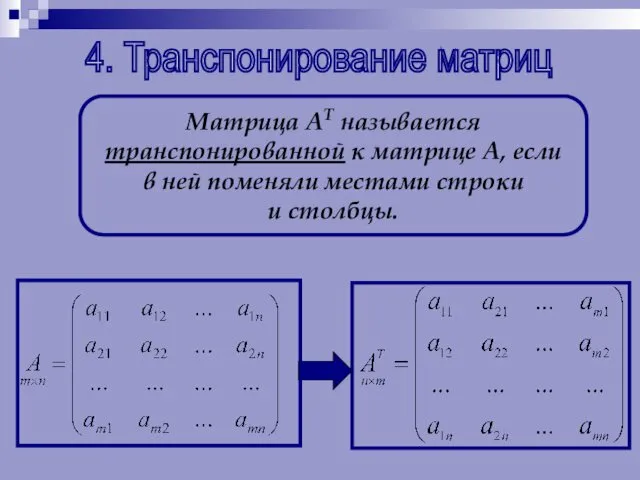
- 28. 4. Транспонирование матриц Матрица АТ называется транспонированной к матрице А, если в ней поменяли местами строки
- 29. (АТ)Т=А (А+В)Т=АТ+ВТ свойства операции траспонирования: 1 2
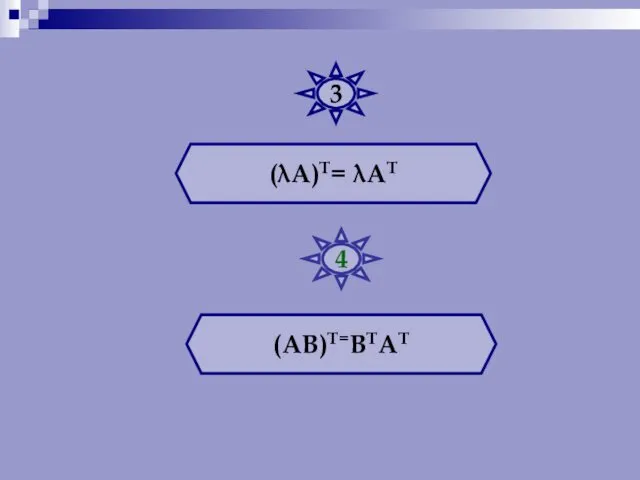
- 30. (λА)Т= λАТ (АВ)Т=ВТАТ 3 4
- 31. Пример. Транспонировать матрицу:
- 32. Решение:
- 33. Определители. Свойства определителей.
- 34. Определителем (детерминантом) матрицы n-го порядка называется число:
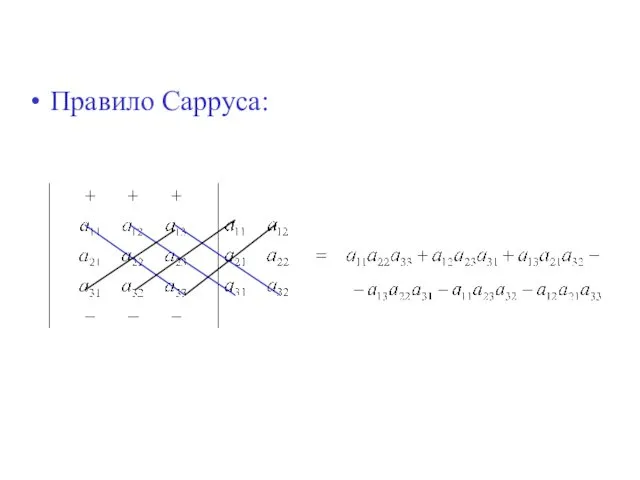
- 37. Правило Сарруса:
- 38. Правило треугольника: « + » « - »
- 39. Примеры:
- 40. Примеры:
- 41. Примеры:
- 42. Свойства определителей. 1. Определитель не изменится, если его транспонировать:
- 43. 2. При перестановке двух строк или столбцов определитель изменит свой знак на противоположный.
- 44. 3. Общий множитель всех элементов строки или столбца можно вынести за знак определителя.
- 46. 4. Определитель с двумя одинаковыми строками или столбцами равен нулю.
- 47. 5. Если все элементы двух строк (или столбцов) определителя пропорциональны, то определитель равен нулю.
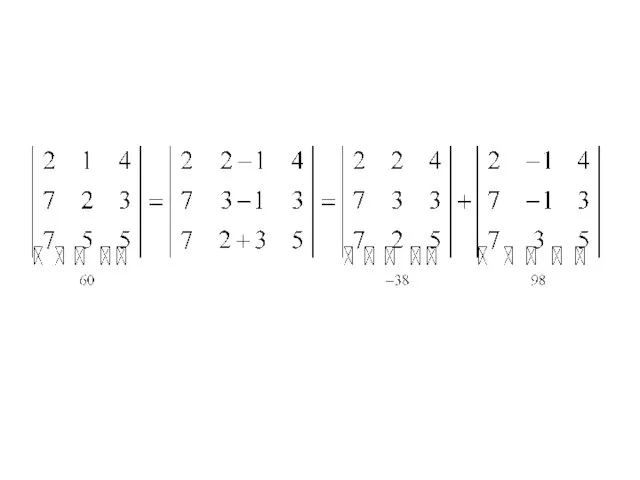
- 48. 6. Если каждый элемент какого-либо ряда определителя представляет собой сумму двух слагаемых, то такой определитель равен
- 51. 7. Если к какой-либо строке (или столбцу) определителя прибавить соответствующие элементы другой строки (или столбца) ,
- 52. ×2 +
- 53. 8. Треугольный определитель равен произведению элементов главной диагонали.
- 54. Привести определитель к треугольному виду и вычислить его: ×(-2) ×(-5) = +
- 55. Разложение определителя по элементам строки или столбца. Минором Mij элемента aij det D называется такой новый
- 57. Для данного определителя найти миноры: М22, М31,М43
- 58. Алгебраическим дополнением Aij элемента aij det D называется минор Mij этого элемента, взятый со знаком т.е.
- 60. Сумма произведений элементов любой строки (или столбца) определителя на их алгебраические дополнения равна этому определителю.
- 61. разложение по i-ой строке: разложение по j-му столбцу:
- 62. Разложить данный определитель по элементам: 1) 3-ей строки; 2) 1-го столбца.
- 63. 1) Разложим данный определитель по элементам 3-ей строки:
- 65. 2) Разложим данный определитель по элементам 1-го столбца:
- 67. Основные методы вычисления определителя. 1. разложение определителя по элементам строки или столбца; 2. метод эффективного понижения
- 68. Метод эффективного понижения порядка: Вычисление определителя n-го порядка сводится к вычислению одного определителя (n-1)-го порядка, сделав
- 69. ×(-3) ×(-1)
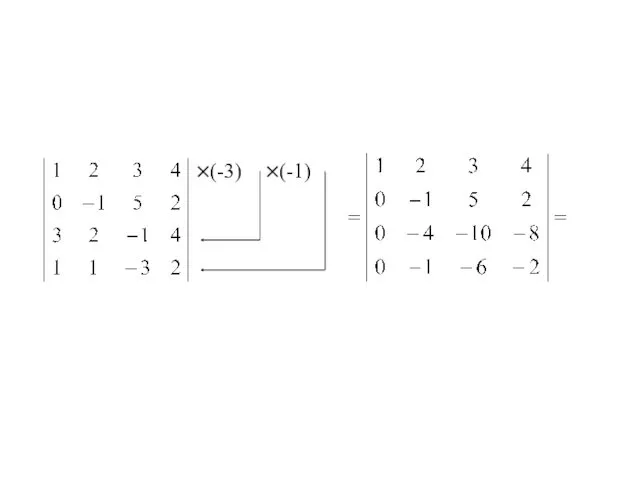
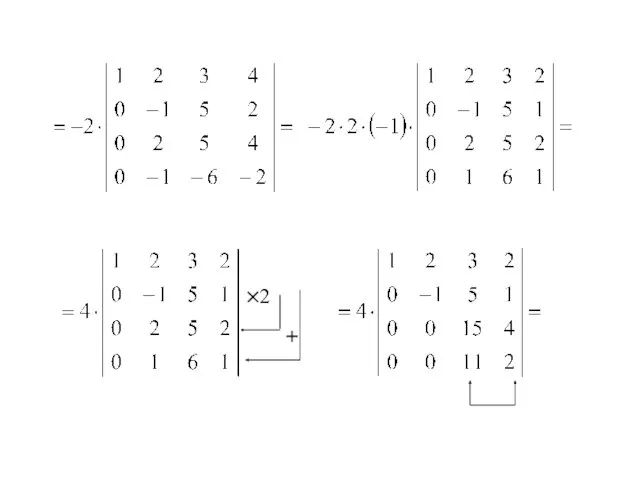
- 71. Вычислить определитель приведением его к треугольному виду. ×(-3) ×(-1)
- 72. ×2 +
- 73. ×(-2)
- 74. Обратная Матрица
- 75. Определение. Матрица называется о б р а т н о й к квадратной матрице , если
- 76. Определение. Матрица, составленная из алгебраических дополнений для элементов исходной матрицы , называется с о ю з
- 77. Формула для нахождения обратной матрицы
- 79. Алгоритм нахождения 1. Находим определитель матрицы А. Он должен быть отличен от нуля. 2. Находим алгебраические
- 80. Пример. Найти матрицу, обратную к матрице:
- 81. Р е ш е н и е. Действуем по алгоритму: 1. Находим определитель матрицы: Определитель отличен
- 82. 2. Находим алгебраические дополнения:
- 84. 3. Составляем союзную матрицу:
- 85. 4. Записываем обратную матрицу по формуле
- 86. 5. Проверка Воспользуемся определением обратной матрицы и найдем произведение
- 87. Задача. Найти матрицу, обратную к данной
- 88. 1. Находим определитель
- 89. 2. Алгебраические дополнения для первой строки:
- 90. Алгебраические дополнения для второй строки:
- 91. Алгебраические дополнения для третьей строки:
- 92. Обратная матрица:
- 93. Элементарные преобразования матриц перестановка строк (столбцов) местами; исключение из матрицы строк (столбцов), состоящих из нулей; умножение
- 95. Скачать презентацию





























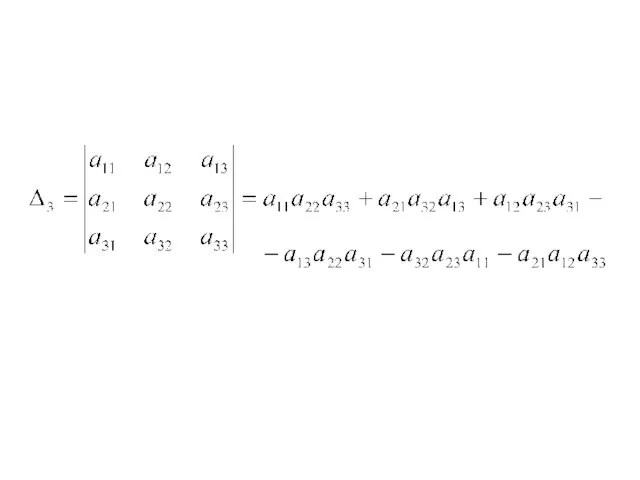













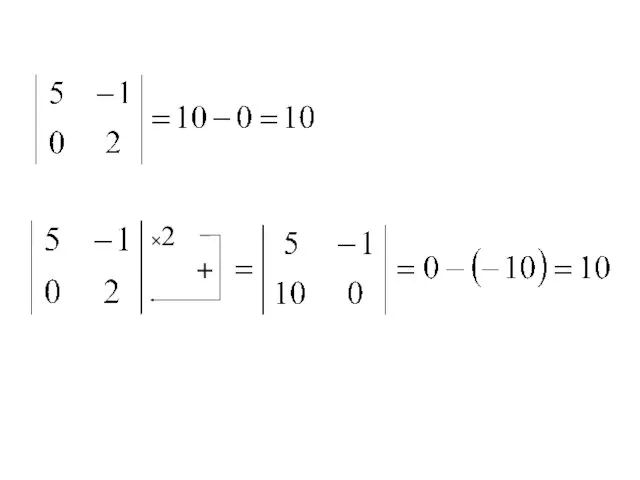



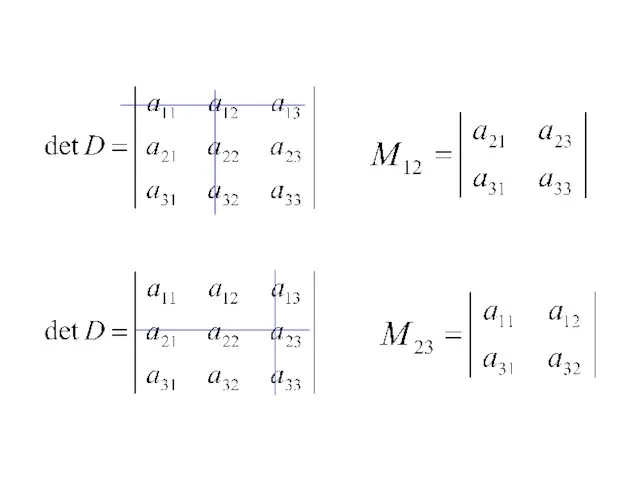


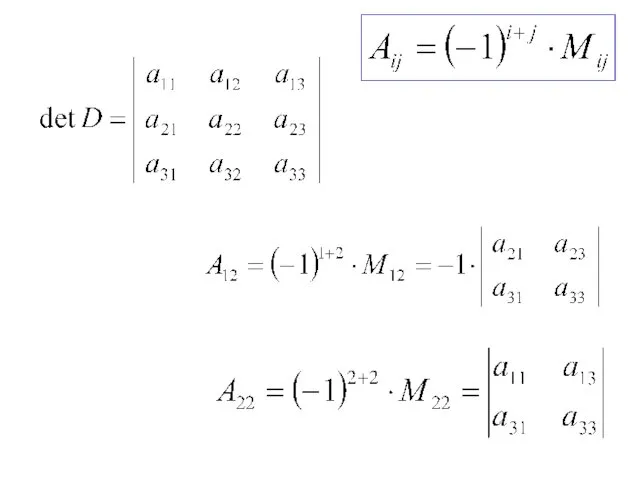

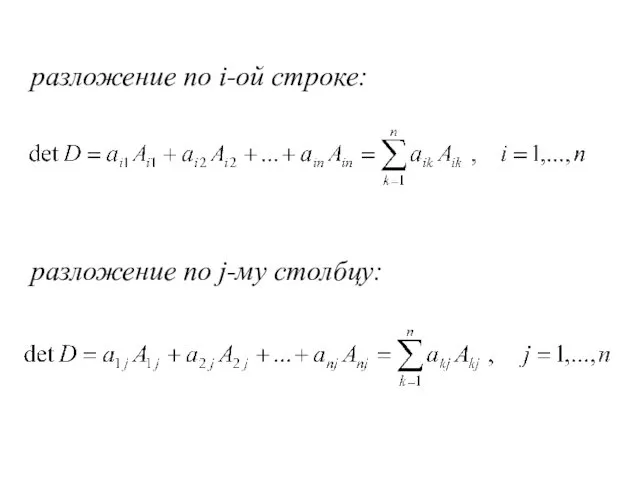


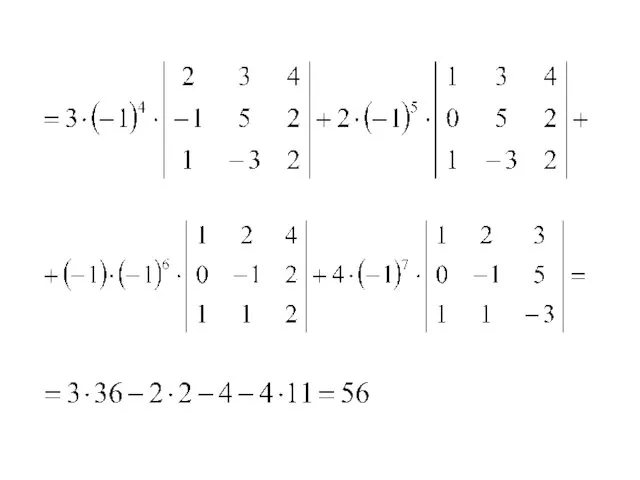

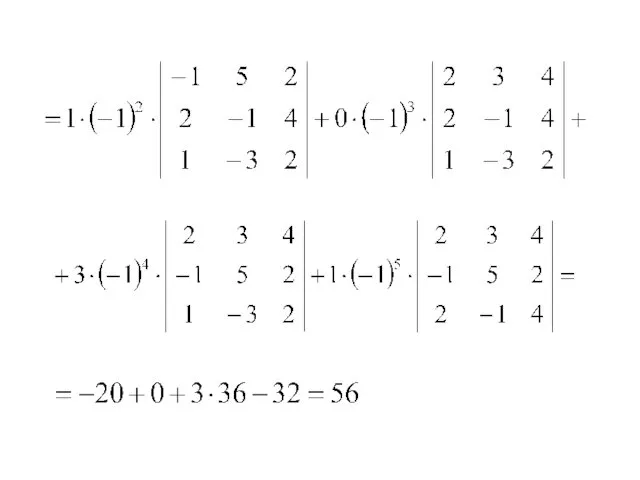


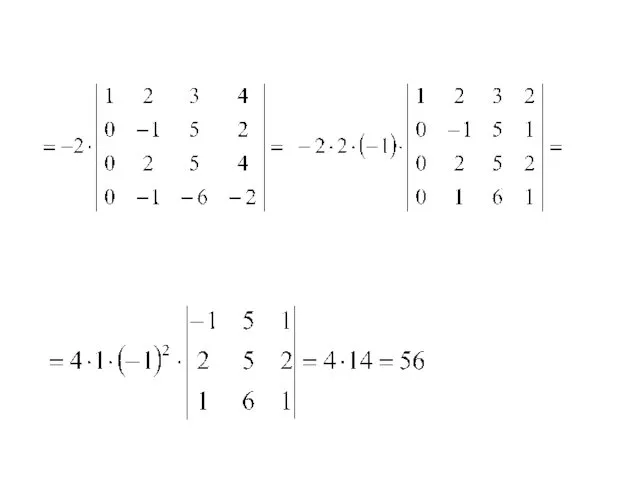






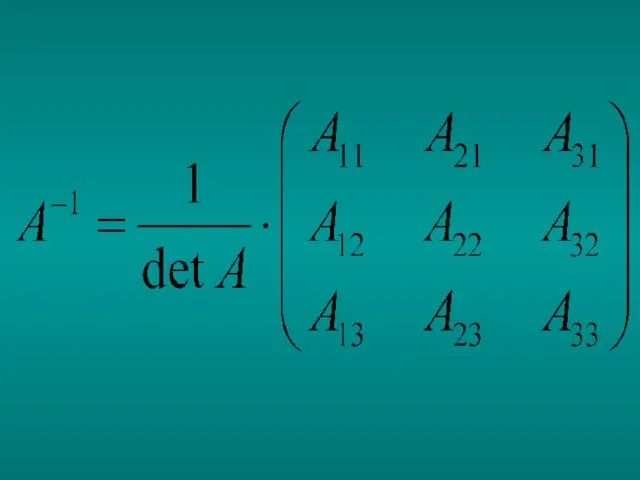




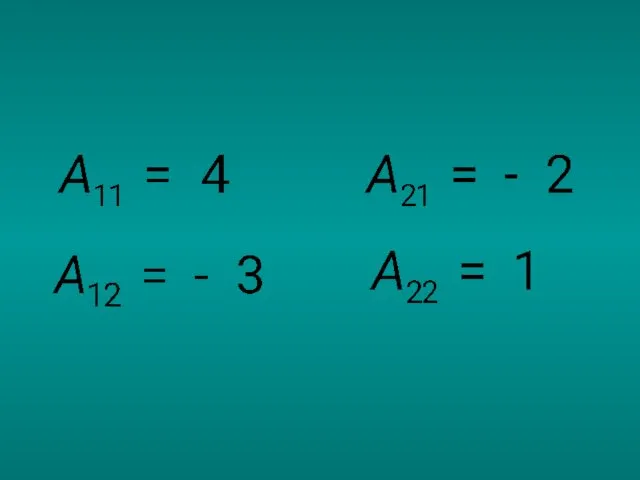










 Деменция. Деммения диагностикасы. Әдістемелік ұсыныстар
Деменция. Деммения диагностикасы. Әдістемелік ұсыныстар Распорядительные документы
Распорядительные документы Использование здоровьесберегающих технологий в работе школьного логопеда
Использование здоровьесберегающих технологий в работе школьного логопеда Центробежные насосы
Центробежные насосы Методы социологических исследований
Методы социологических исследований Компетентностный учитель в образовательном процессе и самореализация обучающихся в современной школе
Компетентностный учитель в образовательном процессе и самореализация обучающихся в современной школе Simulation modeling
Simulation modeling Индия - страна чудес. (10 класс)
Индия - страна чудес. (10 класс) Цепочки
Цепочки BL BOSCH 5.3 ABS. System Description of BL ABS
BL BOSCH 5.3 ABS. System Description of BL ABS Металлургия редких металлов. Вольфрам. Технология производства вольфрама
Металлургия редких металлов. Вольфрам. Технология производства вольфрама Обзор образовательных программ по детской робототехнике
Обзор образовательных программ по детской робототехнике Irregular verbs
Irregular verbs First Conditional. Условное предложение 1 типа. Тест
First Conditional. Условное предложение 1 типа. Тест Ференц Лист (22 окт. 1811-31 июл. 1886)
Ференц Лист (22 окт. 1811-31 июл. 1886) Место СМИ во взаимодействии власти и общества
Место СМИ во взаимодействии власти и общества Монтаж высотных сооружений
Монтаж высотных сооружений Состав числа 14
Состав числа 14 Ауыспалы егістік
Ауыспалы егістік Интересные факты о человеческом мозге
Интересные факты о человеческом мозге Свержение монархии. Февральская революция в России (22.02 - 2.03.1917)
Свержение монархии. Февральская революция в России (22.02 - 2.03.1917) Анатомия нервной системы человека
Анатомия нервной системы человека Студенческий научный кружок кафедры внутренних незаразных болезней, хирургии и акушерства
Студенческий научный кружок кафедры внутренних незаразных болезней, хирургии и акушерства Презентация Творчество Ю.Васнецова. Сказки. Сказка Курочка Ряба
Презентация Творчество Ю.Васнецова. Сказки. Сказка Курочка Ряба Презентация по внеурочной деятельности Уроки ОРИГАМИ как средство активизации творческого потенциала учащихся
Презентация по внеурочной деятельности Уроки ОРИГАМИ как средство активизации творческого потенциала учащихся Соотношение развития, воспитания и формирования личности
Соотношение развития, воспитания и формирования личности Ильменский заповедник
Ильменский заповедник Лесное семеноводство
Лесное семеноводство