Метод интегрирования по частям в неопределенном интеграле. Интегрирование тригонометрических функций презентация
Содержание
- 2. Цели и задачи: Изучить основные методы интегрирования: интегрирование рациональных дробей, интегрирование некоторых классов тригонометрических и иррациональных
- 3. ВОПРОСЫ ЛЕКЦИИ №12 1. Метод интегрирования по частям. 2. Интегрирование некоторых классов тригонометрических функций.
- 4. Литература [1] Н.С. Пискунов. Дифференциальное и интегральное исчисления. Т 1. Москва: Интеграл-Пресс, 2004, с. 340-375. [3]
- 5. УЧЕБНЫЙ ВОПРОС . Интегрирование некоторых классов тригонометрических функций
- 6. Рассмотрим интеграл вида m и n - неотрицательные и по крайней мере одно из них является
- 7. б) б) m и n - неотрицательные чётные, т.е. n=2p, m=2q. Тогда Возведя в степень и
- 8. Вторая разновидность интегралов имеет вид: или Третья разновидность интегралов
- 10. Пример.
- 11. Универсальная тригонометрическая подстановка Всякий интеграл от рациональной функции вида может быть сведён к интегралу от рациональной
- 13. Пример.
- 14. Рассмотрим интегралы вида Для их вычисления используют тригонометрические формулы
- 15. Пример.
- 16. Задание на самостоятельную работу [1] Н.С. Пискунов. Дифференциальное и интегральное исчисления. Т 1. Москва: Интеграл-Пресс, 2004,
- 17. Математика ППИ. НЕОПРЕДЕЛЁННЫЙ ИНТЕГРАЛ Лекция № 13 . Интегрирование дробно-рациональных функций, иррациональных функций. Тригонометрические подстановки.
- 18. ВОПРОСЫ ЛЕКЦИИ №13 1. Интегрирование рациональных дробей. 2.Интегрирование некоторых классов иррациональных функций
- 19. УЧЕБНЫЙ ВОПРОС. Интегрирование рациональных дробей
- 20. Определение. Дробно- рациональной функцией или просто рациональной дробью называется функция, равная частному от деления двух многочленов
- 25. Различают четыре типа простейших рациональных дробей: 1. 2. 3. 4. При этом A, a, M,N, p,
- 26. Интегрирование простейших дробей I и II типов: I. II.
- 27. Интегрирование простейшей дроби III типа Пример. Найти интеграл Решение.
- 28. Теорема. Правильную рациональную дробь , где можно единственным образом разложить в сумму простейших дробей: где -
- 29. Метод неопределённых коэффициентов. Рассмотрим случай, когда корни знаменателя действительные и различные, т.е. рассмотрим правильную дробь: Данную
- 30. 1. Дроби справа приводят к общему знаменателю. 2. Приравнивают числители дробей слева и справа, раскрывают скобки
- 31. Пример. Разложить дробь на простейшие и проинтегрировать.
- 32. Итак,
- 33. УЧЕБНЫЙ ВОПРОС. Интегрирование некоторых классов иррациональных функций
- 34. Интегрирование некоторых классов иррациональных функций С помощью тригонометрических подстановок интегралы от некоторых иррациональных функций приводятся к
- 36. Пример. Найти
- 37. Интеграл
- 38. Интеграл более общего вида
- 39. Пример. 2
- 40. Интегрирование дифференциального бинома
- 41. дробное
- 43. Пример.
- 45. Тригонометрические подстановки С помощью тригонометрических подстановок интегралы от некоторых иррациональных функций приводятся к интегралам от функций,
- 46. В
- 47. Пример.
- 48. Далее (потерян минус в последнем слагаемом):
- 49. Пример. Можно проинтегрировать по частям:
- 50. Пример.
- 55. Понятие об интегралах, не берущихся в элементарных функциях Как мы видим, в дифференциальном исчислении, производная от
- 56. Так, например, хотя по теореме существования для функций существуют первообразные, но они не выражаются в элементарных
- 57. Заключение. В заключение отметим, что рассмотренные методы и приёмы интегрирования не исчерпывают всех классов аналитически интегрируемых
- 58. Контрольные вопросы: 1. В чем заключается метод интегрирования рациональных дробей? 2. Универсальная тригонометрическая подстановка.
- 60. Скачать презентацию


![Литература [1] Н.С. Пискунов. Дифференциальное и интегральное исчисления. Т 1.](/_ipx/f_webp&q_80&fit_contain&s_1440x1080/imagesDir/jpg/47900/slide-3.jpg)







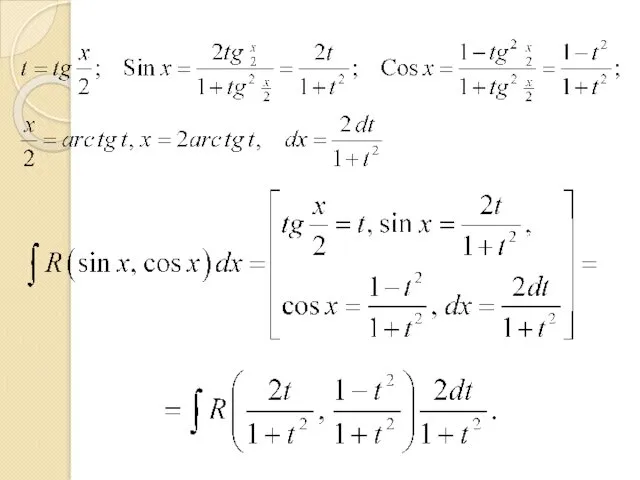



![Задание на самостоятельную работу [1] Н.С. Пискунов. Дифференциальное и интегральное](/_ipx/f_webp&q_80&fit_contain&s_1440x1080/imagesDir/jpg/47900/slide-15.jpg)


















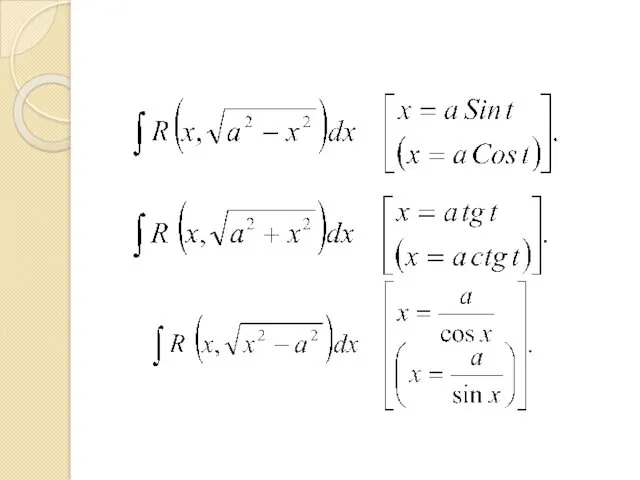








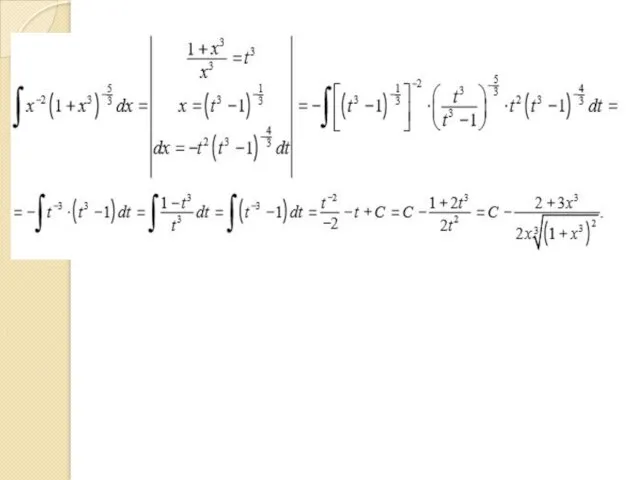

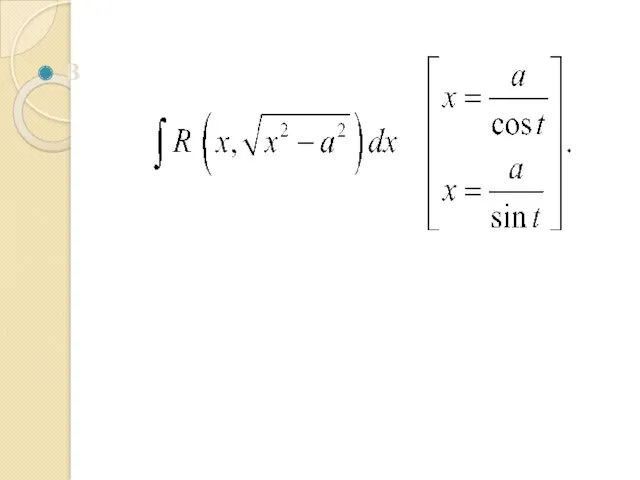




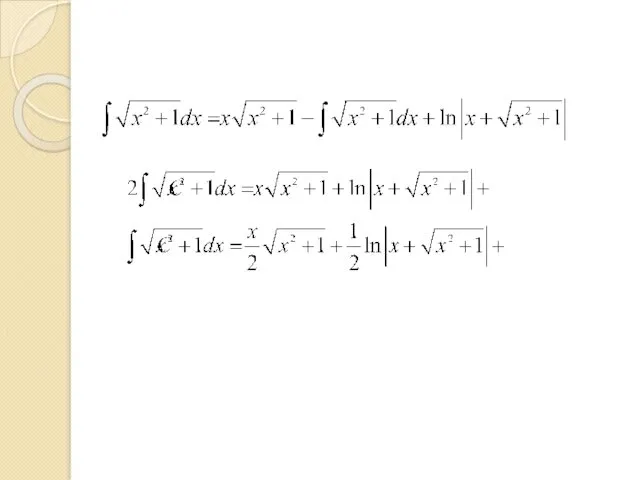







 Органолептический анализ продуктов питания
Органолептический анализ продуктов питания Планирование профессиональной карьеры. Мотивы и потребности
Планирование профессиональной карьеры. Мотивы и потребности АРИНА_ЭБРУ_ПРЕЗЕНТАЦИЯ_2_класс_готовая (1)
АРИНА_ЭБРУ_ПРЕЗЕНТАЦИЯ_2_класс_готовая (1) Зеленый виноград. Презентация к занятию по квиллингу
Зеленый виноград. Презентация к занятию по квиллингу Международные экономические и финансовые организации
Международные экономические и финансовые организации Презентация: Качество питьевой воды и здоровье
Презентация: Качество питьевой воды и здоровье Николай Николаевич Носов
Николай Николаевич Носов Классификация профессий. Основные понятия
Классификация профессий. Основные понятия Желудочно-кишечные кровотечения. Часть II
Желудочно-кишечные кровотечения. Часть II Михаил Юрьевич Лермонтов (1814 – 1841)
Михаил Юрьевич Лермонтов (1814 – 1841) Классный час в 5 классе по теме: Что мы должны знать о ПАВ
Классный час в 5 классе по теме: Что мы должны знать о ПАВ Электровакуумные приборы
Электровакуумные приборы Мифологические существа в славянской мифологии: Баба-Яга
Мифологические существа в славянской мифологии: Баба-Яга Электрообработка деталей машины
Электрообработка деталей машины Санкт-Петербург. Визитная карточка города
Санкт-Петербург. Визитная карточка города Разработка зоны отдыха на берегу р.Кондома в районе Малышев Лог
Разработка зоны отдыха на берегу р.Кондома в районе Малышев Лог Zaha Hadid
Zaha Hadid Развитие речи детей раннего возраста
Развитие речи детей раннего возраста Уважаемые дамы, купите собаку
Уважаемые дамы, купите собаку Землеустрій житлової забудови на прикладім міста Фастів
Землеустрій житлової забудови на прикладім міста Фастів Экосистема 2050. Компания лидеров
Экосистема 2050. Компания лидеров Александр Македонский
Александр Македонский Применение активных методов обучения в начальной школе
Применение активных методов обучения в начальной школе Технические условия на переоборудование и перепланировку помещения
Технические условия на переоборудование и перепланировку помещения День народного единения
День народного единения Герой й неповторимой эпохи
Герой й неповторимой эпохи Что мы знаем о хлебе?
Что мы знаем о хлебе? Стоп Корона. Угадай звезду под маской
Стоп Корона. Угадай звезду под маской