Содержание
- 2. Еще немного об IDEF0 Вернёмся к последним двум слайдам предыдущей лекции.
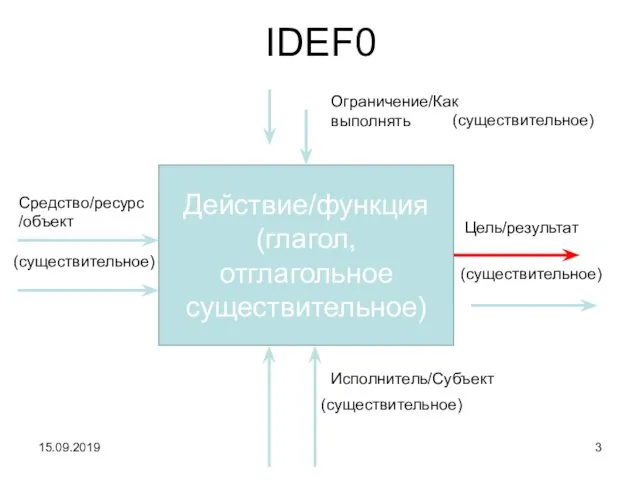
- 3. IDEF0 Действие/функция (глагол, отглагольное существительное) Цель/результат Средство/ресурс/объект Исполнитель/Субъект Ограничение/Как выполнять (существительное) (существительное) (существительное) (существительное) 15.09.2019
- 4. Методика создания диаграммы IDEF0 Уровень 0: (*) Нарисовать и подписать прямоугольник (назвать функцию системы) Указать цель
- 5. НЕ ДОПУСКАЕТСЯ (НЕЛЬЗЯ!!!): 1. Отсутствие у функции одновременно стрелок управления и входа не допускается. Это означает,
- 6. 2 (НЕЛЬЗЯ!!). У каждого блока должен быть как минимум один выход. Пример: Функция без выхода
- 7. Рассмотрим пример.
- 9. Укажем некоторые недостатки этих диаграмм (несбалансированность контекстной диаграммы, Недочёты в дочерней ( «Должностные инструкции» и определения
- 10. Тема 2. МЕТОДЫ ОПИСАНИЯ СЛОЖНЫХ СИСТЕМ
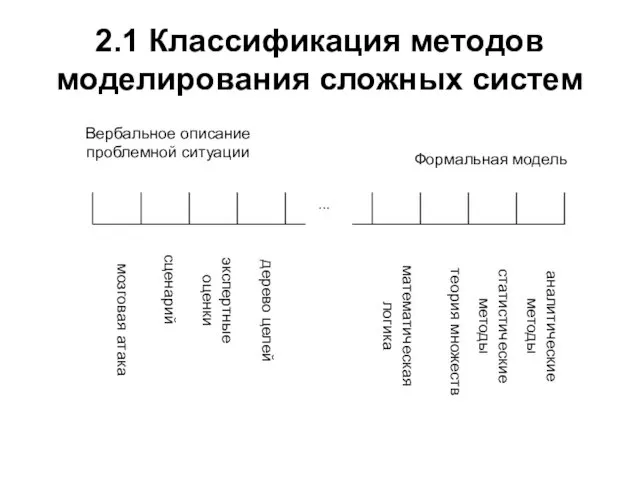
- 11. 2.1 Классификация методов моделирования сложных систем
- 13. 2.2 Методы направленные на активизацию использования интуиции и опыта специалистов Методы типа «мозговой атаки» или коллективной
- 14. Методы типа «сценариев». Методы подготовки и согласования представлений о проблеме или анализируемом объекте, изложенных в письменном
- 15. Сценарий предусматривает не только содержательные суждения, помогающие не упустить детали, которые невозможно учесть в формальной модели
- 16. Методы типа «Дельфи». Основные средства повышения объективности результатов при применении метода «Дельфи» – использование обратной связи,
- 17. Методы экспертных оценок. Основные этапы методов экспертных оценок заключаются в следующем: формирование экспертных групп, включая требования
- 18. Пример Предположим, например, что эксперты оценивают альтернативы в числовых шкалах. Пусть – оценка i-й альтернативы j-м
- 19. Если альтернативы нельзя оценить сразу одним числом и экспертам предлагается дать оценки отдельно по каждому показателю.
- 20. Определение коэффициента компетентности j-го эксперта можно поручить самим экспертам. Пусть каждый из них (l-й) оценивает компетентность
- 21. При обработке материалов коллективной экспертной оценки используются методы теории ранговой корреляции. Для оценки степени согласованности мнений
- 22. - количество рассматриваемых свойств; - место, которое заняло i-е свойство в ранжировке j-м экспертом; - отклонение
- 23. Пример на доске – 3 эксперта, 4 цвета, матрица предпочтений 3х4 Сильная несогласованность 3 1 2
- 24. Методы структуризации. Структурные представления разного рода позволяют разделить сложную проблему с большой неопределенностью на более мелкие,
- 25. Методы типа «дерева целей». Термин «дерево» подразумевает использование иерархической структуры, получаемой путем расчленения общей цели на
- 26. Морфологические методы. Основная идея морфологического подхода − систематически находить все возможные варианты решения поставленной проблемы или
- 27. 2.3 Методы формализованного представления систем Классификация . Выделяют следующие обобщенные группы (классы) методов: аналитические (методы классической
- 28. теоретико-множественные, логические, лингвистические, семиотические представления (методы дискретной математики), составляющие теоретическую основу разработки языков моделирования, автоматизации проектирования,
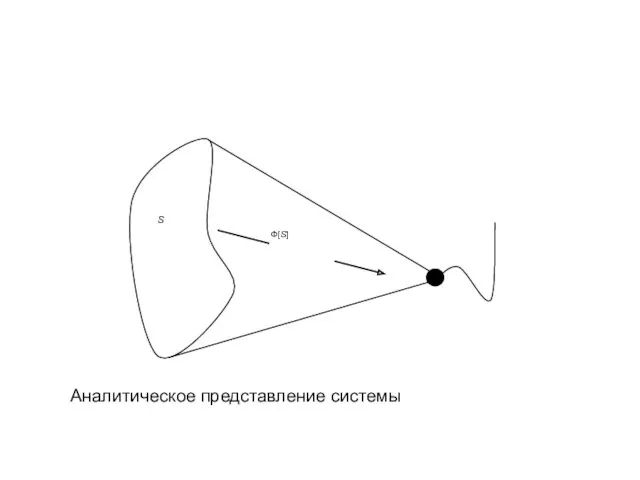
- 29. 1. Аналитические методы. Аналитическими в рассматриваемой классификации названы методы, которые отображают свойства реальных объектов и процессов
- 30. Аналитическое представление системы
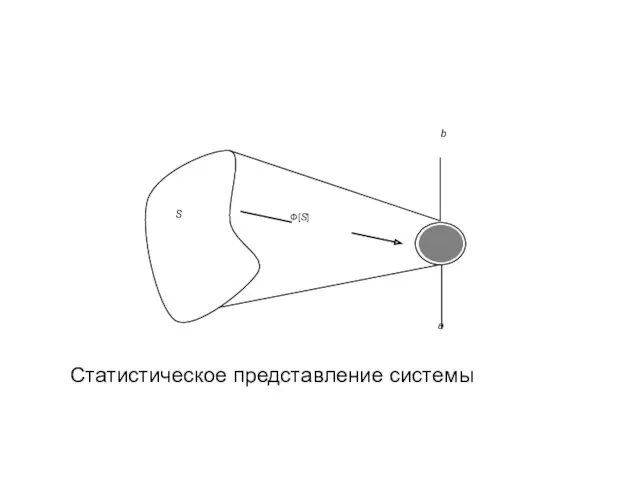
- 31. Статистические методы. Статистическим представлением называют отображение системы с помощью случайных (стохастических) событий, процессов, которые описываются вероятностными
- 32. Статистическое представление системы
- 33. На базе статистических представлений развивается ряд математических теорий: математическая статистика, объединяющая различные методы статистического анализа (регрессионный,
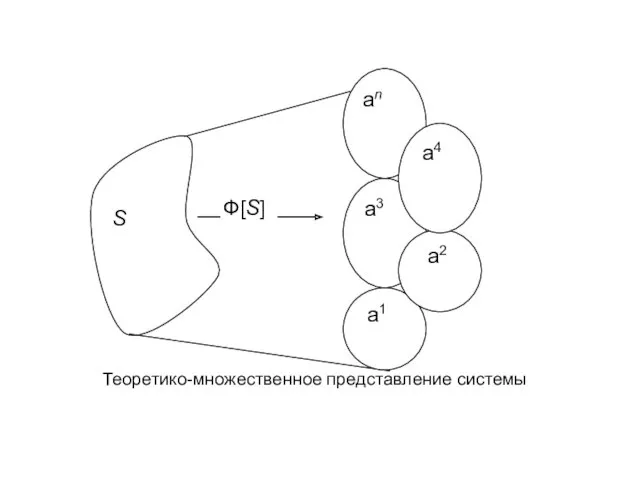
- 34. Теоретико-множественные представления. Теоретико-множественные представления базируются на понятиях множество, элементы множества, отношения на множествах. Сложную систему можно
- 35. Теоретико-множественное представление системы
- 36. Благодаря тому что при теоретико-множественных представлениях систем и процессов в них можно вводить любые отношения, эти
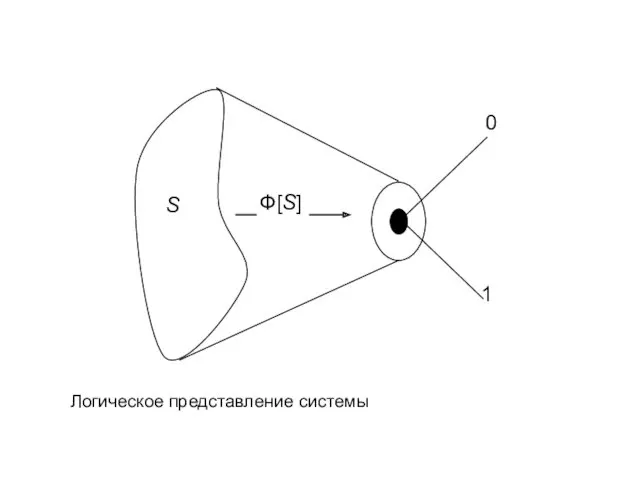
- 37. Математическая логика. Логические представления переводят реальную систему и отношения в ней на язык одой из алгебр
- 38. Логическое представление системы
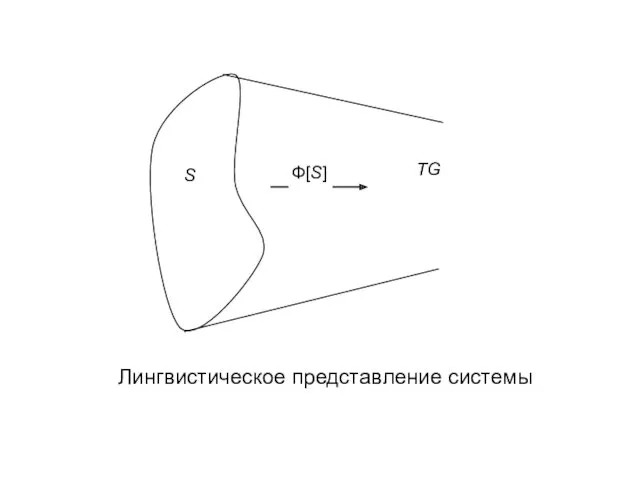
- 39. Лингвистические, семиотические представления. Лингвистические представления (рис. 2.10) базируются на понятиях тезауруса Т (множество смысловыражающих элементов языка
- 40. Лингвистическое представление системы
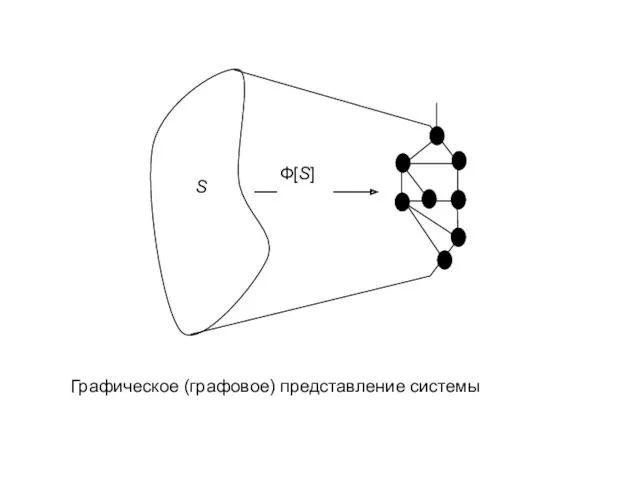
- 41. Графические представления. К графическим представлениям (рис. 2.11) отнесены любые графики (графики Ганта, диаграммы, гистограммы и т.д.)
- 42. Графическое (графовое) представление системы
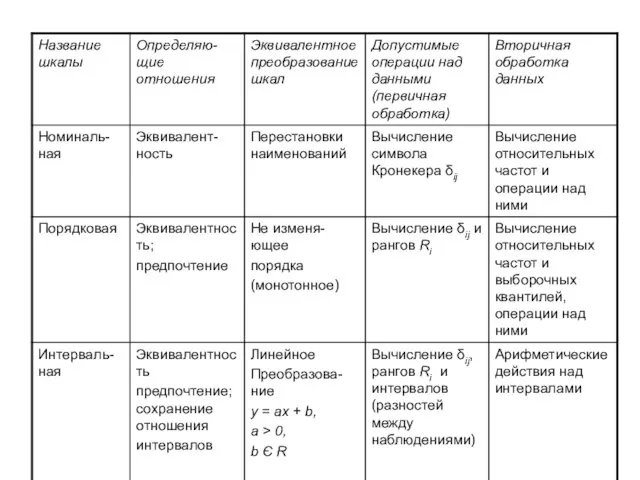
- 43. 2.4 Измерительные шкалы В современной теории измерений определено, что измерение – это алгоритмическая операция, которая данному
- 44. Рассматриваются только такие системы, про любые два состояния которых можно сказать, различимы они или нет, и
- 45. Шкалы наименований. Предположим, что число различимых состояний (или, как говорят математики, – число классов эквивалентности) конечно.
- 46. Перейдем теперь к вопросу о допустимых операциях над данными, выраженными в номинальной шкале. Подчеркнем еще раз,
- 47. Пример номинальной шкалы – номер спортсмена на майке
- 48. При обработке экспериментальных данных, зафиксированных в номинальной шкале, непосредственно с самими данными можно выполнять только операцию
- 49. Можно: сравнивать эти частоты между собой (находя, например, моду – номер наиболее часто встречающегося класса выполнять
- 50. Порядковые шкалы. Следующей по силе за номинальной шкалой является порядковая шкала (используется также название ранговая шкала).
- 51. Операция проверки отношения предпочтения может быть формализована. Введем индикаторную функцию C(t) положительных чисел: . Тогда если
- 52. Модифицированные порядковые шкалы. По-видимому, опыт работы с сильными числовыми шкалами и желание уменьшить относительность порядковых шкал,
- 53. Шкала твердости по Моосу. Из двух минералов тверже тот, который оставляет на другом царапины или вмятины
- 54. Балльные шкалы оценки знаний учащихся – порядковая шкала!!. Слушая ответы учащихся или сравнивая их письменные работы,
- 55. Шкалы интервалов Пусть М – множество совершенно упорядоченных элементов, для каждой пары с, d которых задано
- 56. В шкале интервалов можно ввести систему координат. Выберем для этого любую пару точек (репер) ; точка
- 57. Если ввести в М другую систему координат, построенную на репере с1 и d1, то координаты хe
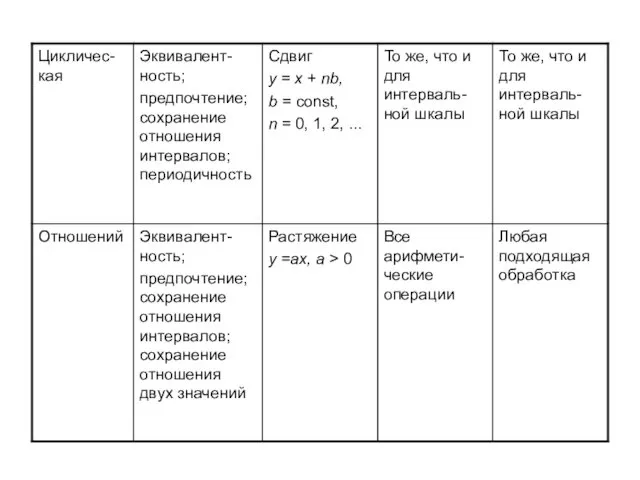
- 58. Шкалы отношений. Пусть наблюдаемые величины удовлетворяют не только аксиомам упорядоченности (2.4) и (2.5), но и аксиомам
- 59. Шкалы разностей. К числу шкал, единственных с точностью до линейных преобразований, относятся шкала интервалов ( ,
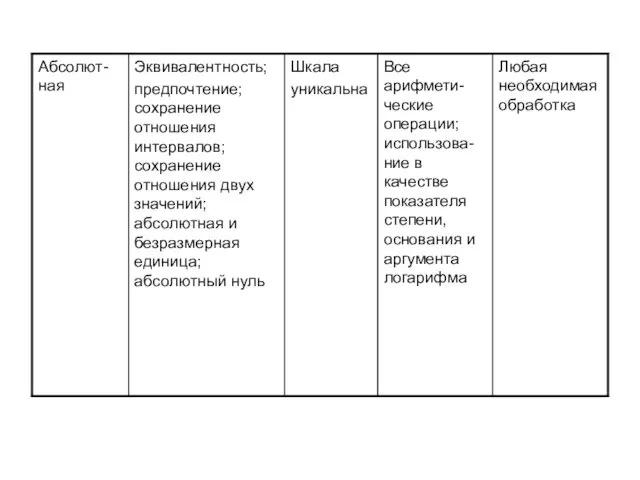
- 60. Абсолютная шкала. Рассмотрим такую шкалу, которая имеет и абсолютный нуль, и абсолютную единицу. Эта шкала не
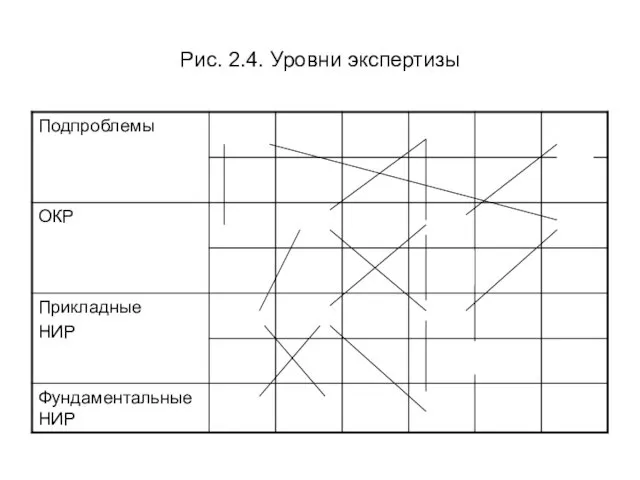
- 64. Метод решающих матриц (опционально) Обозначим относительные веса направлений (подпроблем) составим план опытно-конструкторских работ и оценим их
- 65. Рис. 2.4. Уровни экспертизы
- 66. В методе решающих матриц относительные веса определяются в процентах и нормируются по отношению к 100: Экспертами
- 68. Скачать презентацию





















































 Институциональные основы функционирования рыночной экономики
Институциональные основы функционирования рыночной экономики Создание бульвара по улице Школьная
Создание бульвара по улице Школьная Планета Уран
Планета Уран Шаблоны презентаций по ИЗО
Шаблоны презентаций по ИЗО Мой герой войны
Мой герой войны Силовая схема МПД
Силовая схема МПД Болезнь Альцгеймера
Болезнь Альцгеймера Заводы Санкт-Петербурга
Заводы Санкт-Петербурга Автоматизация конвейерной линии в условиях ОАО Шахтоуправление Анжерское
Автоматизация конвейерной линии в условиях ОАО Шахтоуправление Анжерское Урок в 9 классе. Тема: Аммиак
Урок в 9 классе. Тема: Аммиак Здоровье сберегающий проект ЗОЖ меню
Здоровье сберегающий проект ЗОЖ меню Экономические реформы в период перестройки 1985-1991 гг
Экономические реформы в период перестройки 1985-1991 гг Вирощування печериць з використанням енергозберігаючих технологій
Вирощування печериць з використанням енергозберігаючих технологій Движение связанных тел
Движение связанных тел Презентация Внеурочная деятельность
Презентация Внеурочная деятельность Формы организации обучения. Урок, структура урока, требования к уроку
Формы организации обучения. Урок, структура урока, требования к уроку Бухгалтерский (финансовый) учёт
Бухгалтерский (финансовый) учёт Презентация. НОД развитие речи в подготовительной к школе группе.
Презентация. НОД развитие речи в подготовительной к школе группе. Развитие арабской медицины
Развитие арабской медицины Внутреннее строение Земли. Строение литосферы
Внутреннее строение Земли. Строение литосферы Результаты выращивания форели в условиях КФХ Горное
Результаты выращивания форели в условиях КФХ Горное Балки покрытия
Балки покрытия Marpol and other legal requirements for the protection of the environment
Marpol and other legal requirements for the protection of the environment Выбор ВУЗа. Алгоритм действий будущего абитуриента
Выбор ВУЗа. Алгоритм действий будущего абитуриента Презентация Использование игр в развитии детей, имеющих патологию речи
Презентация Использование игр в развитии детей, имеющих патологию речи Басқару объектісінің математикалық моделдері
Басқару объектісінің математикалық моделдері Зерновые яровые культуры
Зерновые яровые культуры Внутренняя улыбка. Способы сохранения состояния внутренняя улыбка (часть 2)
Внутренняя улыбка. Способы сохранения состояния внутренняя улыбка (часть 2)