Слайд 2СРЕДНИЕ ВЕЛИЧИНЫ.
Средняя – это обобщающая характеристика выборочной совокупности, исчисляемая для однородных статистических совокупностей,
которая имеет двойственный характер.
Слайд 3 Для данной совокупности средняя величина является конкретной величиной, но в отношении индивидуальных значений
признаков средняя является величиной абстрактной.
Средние бывают двух видов:
1. Средние объема
2. Структурные средние.
Слайд 4Формула степенной средней,
Служит базой для исчисления всех средних объемов.
Формула конкретной средней
зависит от показателя степени Z.
Слайд 5Формулы исчисления некоторых средних объема:
Слайд 6Средняя гармоническая
применяется в тех случаях, когда в ряду распределения представлены не отдельно варианты,
а их произведения.
Слайд 7Средняя геометрическая
применяется в рядах динамики для расчетов среднего коэффициента роста и прироста.
Слайд 8Средняя арифметическая простая
применяется в двух случаях:
- если известен ряд не сгруппированных данных, в
которых число наблюдений равно числу элементов.
- если имеется вариационный ряд, в котором частоты равны между собой.
Слайд 9Средняя арифметическая взвешенная
применяется если в представленном вариационном ряду частоты не равны между собой.
Слайд 10ПРИМЕР 1
Определите средний стаж работников предприятия,если известно
Слайд 12ПРИМЕР 2
Определите среднюю процентную ставку по каждому виду кредита по следующим данным:
Слайд 14ПРИМЕР 3
Определите среднюю внешнеторговую цену товара А, по данным
Слайд 16Расчет средних величин в интервальных рядах распределения.
Рассчитать по имеющимся данным средний объем полученного
кредита предприятиями отрасли,моду медиану, дециль,коэффициент дифференциации, все показатели вариаций.
Слайд 19Расчет средних величин в интервальных рядах распределения.
Для познания статистической совокупности применяются следующие структурные
средние:
- мода;
- медиана;
- квартель;
- квантель;
- дециль;
- продциль.
Слайд 20Мода
это значение признака, которое чаще всего встречается в ряду распределения.
Используется в торговле.
В интервальном ряду распределения мода рассчитывается по следующей формуле:
Слайд 21где X mo – нижняя граница модального интервала;
i Mo – величина модального интервала;
f
Mo - модальная максимальная частота;
f Mo-1 – частота, предшествующая модальной;
f Mo+1 – частота, следующая за модальной.
Мо=5+(7-5)*(21-3)/(2*21+3-12)=6,36 тыс.$
Вывод:чаще всего встречаются автомобили со стоимостью 6,36 тыс.$
Слайд 22Медиана
средняя обобщающая характеристика, которая делит всю совокупность на две равные части, причем
первая часть должна иметь значения больше, чем средний вариант, а другая меньше.
В интервальном ряду распределения медиана рассчитывается по специальной формуле:
Слайд 23где X Me – нижняя граница медиального интервала;
i Me – величина медиального интервала;
f
Me – медиальная частота, которая находится там, где есть половина всех частот;
S Me-1 = сумма накопленных частот до медиальной частоты.
Ме=5+2(50/2-92+3))/21=6,9 тыс.$
Вывод:половина автомобилей имеет стоимость 6,9 тыс.$ ,а другая половина больше.
Слайд 24Дециль
средняя обобщающая характеристика, которая делит всю совокупность на 10 разных частей.
Нижний
дециль показывает средний признак для 10 % минимальных значений. Частота нижнего дециля будет находиться там, где будет находиться 10% частот. Частота верхнего дециля будет находиться там, где будет находиться 9/10 всей суммы частот.
Слайд 25Производится расчет нижнего и верхнего дециля.
Нижний дециль = d1 и рассчитывается по формуле:
Верхний
дециль = d9 и рассчитывается по формуле:
Слайд 26Децильный коэффициент
дифференциации
Слайд 27Показатели вариации
Для изучения строения статистической совокупности, для оценки ее однородности и расчетов насколько
точной является представленная средняя величина, рассчитывают показатели вариации.
Показатели вариации характеризуются абсолютными, относительными и средними величинами.
Слайд 29Размах вариаций
Это разница между максимальным и минимальным показателями.
R=max-min
R=10-2=8 тыс. долларов
Слайд 30Среднее линейное отклонение
Применяется в экономических расчетах для характеристики территориальных и региональных различий и
показывает насколько каждый признак отклоняется от средней величины.
– на эту сумму в среднем отличается каждый признак.
Слайд 31Дисперсия
Более объективно отражает меру вариаций в статистике на практике.
Слайд 32Среднее квадратическое отклонение
Является мерилом надежности средней. Чем меньше среднее квадратическое отклонение, тем точнее
среднее представляет собой всю статистическую совокупность.
Слайд 33Коэффициент вариации
Относительный показатель, который характеризует вариацию.
Если , то колеблемость показателя слабая, от 10%
до 30% - умеренная, >30% - высокая.
Слайд 34При расчете дисперсии по интервальному ряду распределения с равными интервалами вычисления можно производить
по способу расчета от условного 0 или способу моментов по следующим формулам:
i – величина интервала
А – любое число в ряду распределения, которое как правило находится или в середине ряда или имеет наибольшую частоту.
Слайд 35Расчет дисперсии по способу моментов проводится по следующей формуле:
где
Слайд 36Общая дисперсия
Показывает изменчивость признака, вызванную за счет группировочного признака и дисперсии, возникающие в
каждой отдельной группе
Слайд 37Межгрупповая дисперсия
Обуславливает вариацию результативного признака за счет группировочного и рассчитывают по следующей формуле:
где
- среднее, исчисленное в каждой группе
- среднее, исчисленной для всей статистической совокупности
Слайд 38Среднее из групповых дисперсий
Характеризует случайную вариацию в каждой отдельной группе и рассчитывается по
следующей формуле:
где
- частная или групповая дисперсия, которая рассчитывается:
Слайд 39Правило сложения дисперсий
По правилу сложения дисперсий общая дисперсия представляет собой сумму из межгрупповой
и средней из групповых дисперсий:
Слайд 40Эмпирическое корреляционное отношение
Для характеристики тесноты связи между группировочными и результативными признаками применяется эмпирическое
корреляционное отношение, которое рассчитывается:
Если показатель тесноты связи находится в пределах от 0,1 до 0,3, то связь слабая; 0,3-0,5 – умеренная; от 0,5 до 0,7 – заметная; 0,7–0,9 – тесная; 0,9–0,99 – весьма тесная.
Слайд 41Коэффициент детерминации
Коэффициент детерминации – показывает долю межгрупповой дисперсии в общей дисперсии результативного признака
и характеризует силу влияния группировочного признака на образование общей вариации. Это эмпирическое корреляционное отношение в квадрате:
Слайд 42Пример 4:
Определите тесноту связи между формой собственности банка и размером его капитала, рассчитав
эмпирическое корреляционное отношение и коэффициент детерминации по следующим данным:
Слайд 43Определите тесноту связи между территориальным расположением и количеством таможенных постов, рассчитав эмпирическое корреляционное
отношение и коэффициент детерминации по следующим данным:
Слайд 44Расчеты:
Коэффициент детерминации – это эмпирическое корреляционное отношение в квадрате:
Показывает, что на 12%
вариация капитала обусловлена различиями в форме собственности и на 88% зависит от влияния прочих факторов.
 Отчет работы участка обслуживанию клапанов и навесного оборудования
Отчет работы участка обслуживанию клапанов и навесного оборудования Строение семян растений
Строение семян растений Задания по математике. (Вариант 6)
Задания по математике. (Вариант 6) Классификация холодильных машин
Классификация холодильных машин Автоматизация звука Ш. Презентация Искатель.
Автоматизация звука Ш. Презентация Искатель. Электромагнитное взаимодействие
Электромагнитное взаимодействие 12 апреля – День космонавтики
12 апреля – День космонавтики педсовет в ДОУ Инновационная деятельность как условие формирования профессиональной компетентности педагогов ДОУ.
педсовет в ДОУ Инновационная деятельность как условие формирования профессиональной компетентности педагогов ДОУ. У Лукоморья дуб зеленый
У Лукоморья дуб зеленый Биологические ритмы в жизни человека
Биологические ритмы в жизни человека Итоги деятельности центра здоровья для детей
Итоги деятельности центра здоровья для детей Rotacyzm. Deformacja (rotacyzm właściwy)
Rotacyzm. Deformacja (rotacyzm właściwy) Основы безопасности информационных технологий. Виртуальные частные сети
Основы безопасности информационных технологий. Виртуальные частные сети Природа и архитектура. Организация архитектурноландшафтного пространства
Природа и архитектура. Организация архитектурноландшафтного пространства Презентация к уроку Справедливость
Презентация к уроку Справедливость Блокада Ленинграда
Блокада Ленинграда Презентация к уроку С днем Победы. Открытка
Презентация к уроку С днем Победы. Открытка Составление текста по сюжетным картинкам
Составление текста по сюжетным картинкам Не так живи, как хочется, а так живи, как Бог велит
Не так живи, как хочется, а так живи, как Бог велит Гражданское право Российской Федерации
Гражданское право Российской Федерации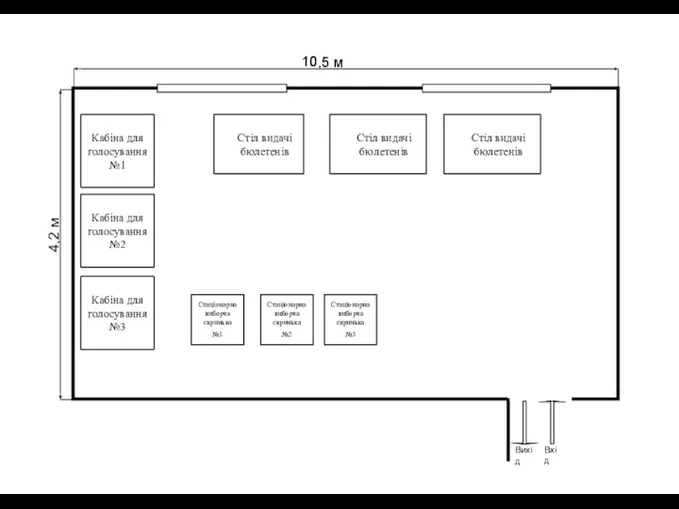 План приміщення для голосування
План приміщення для голосування Владимир Семёнович Высоцкий (1938 – 1980)
Владимир Семёнович Высоцкий (1938 – 1980) Производство – основа экономики
Производство – основа экономики О состоянии и об охране окружающей среды в Тверской области
О состоянии и об охране окружающей среды в Тверской области Анестезиология и реаниматология. Кислотно-щелочное равновесие. Клинические варианты нарушений
Анестезиология и реаниматология. Кислотно-щелочное равновесие. Клинические варианты нарушений Организационное заседание ШНО.
Организационное заседание ШНО. Исследование скважин и пластов
Исследование скважин и пластов Противоэпидемические мероприятия в очагах с фекальнооральным механизмом передачи
Противоэпидемические мероприятия в очагах с фекальнооральным механизмом передачи