Содержание
- 2. Литература Высшая математика: учебное пособие / В.И. Белоусова, Г.М. Ермакова, М.М. Михалева, Н.В. Чуксина, И.А. Шестакова
- 3. Понтрягин ЛС Обыкновенные ДУ. – М, 1961. Филлипов АФ Сборник задач по ДУ. – М, 2008.
- 4. Дифференциальные уравнения Любой процесс, в котором есть движение, описывается ДУ §1. Основная терминология дифференциальных уравнений Уравнение,
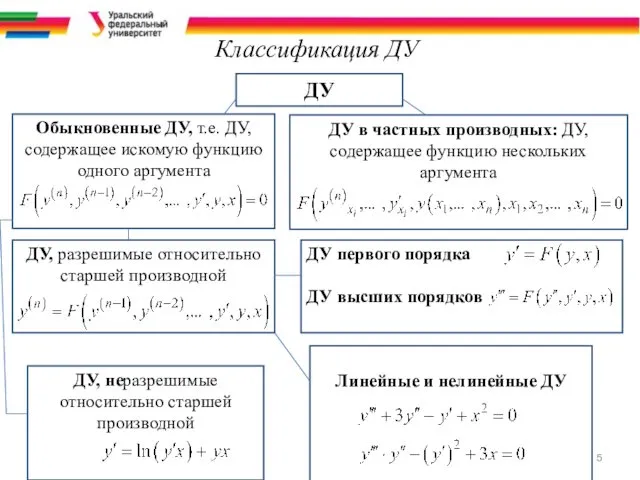
- 5. Классификация ДУ ДУ ДУ, разрешимые относительно старшей производной Обыкновенные ДУ, т.е. ДУ, содержащее искомую функцию одного
- 6. В данном курсе будут рассматриваться только обыкновенные дифференциальные уравнения, разрешенные относительно старшей производной, т. е. уравнения
- 7. Основная задача теории ДУ: решить ДУ, т. е. найти все его решения и описать их свойства.
- 8. Методы решения ДУ: Точные (аналитические). Приближенные Численные Графические
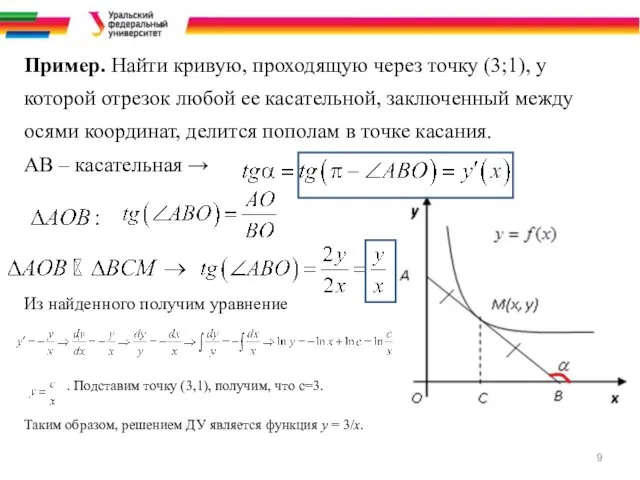
- 9. Пример. Найти кривую, проходящую через точку (3;1), у которой отрезок любой ее касательной, заключенный между осями
- 10. §2. Дифференциальные уравнения первого порядка. Дифференциальное уравнение первого порядка имеет вид: F(x, y, y')=0, где x
- 11. Например, уравнение y' = x2/y можно записать в виде dy/dx = x2/y или x2 dx −
- 12. Чтобы получить одно решение дифференциального уравнения, необходимо подчинить его некоторым дополнительным условиям. Условие, что функция у(х)
- 13. Общим решением дифференциального уравнения первого порядка называется функция у = φ(х, С), содержащая одну произвольную постоянную
- 14. С геометрической точки зрения общее решение дифференциального уравнения есть семейство интегральных кривых на плоскости Оху; частное
- 15. Теорема (существования и единственности решения задачи Коши). Если в уравнении y' = f(x, y) функция f(x,
- 16. В процессе решения дифференциального уравнения нередко приходят к соотношению вида Ф(х, у, С) = 0, которое
- 17. Пример: рассмотрим уравнение – общее решение; – частное решение; у≡0 – особое решение ДУ.
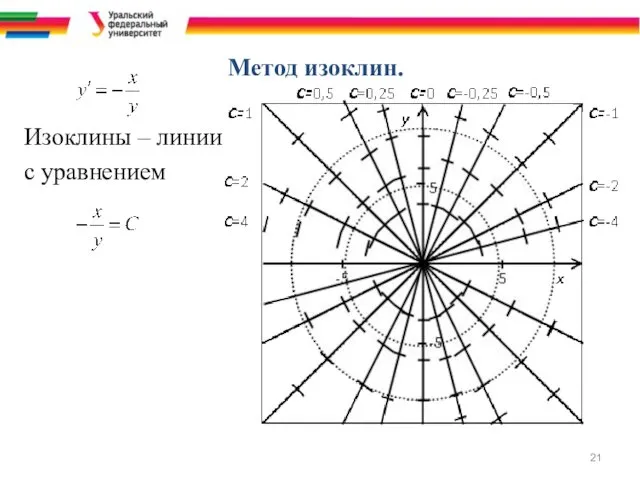
- 18. Геометрический метод решения. Метод изоклин. Уравнение y' = f(x, y) в каждой точке (x, y) области
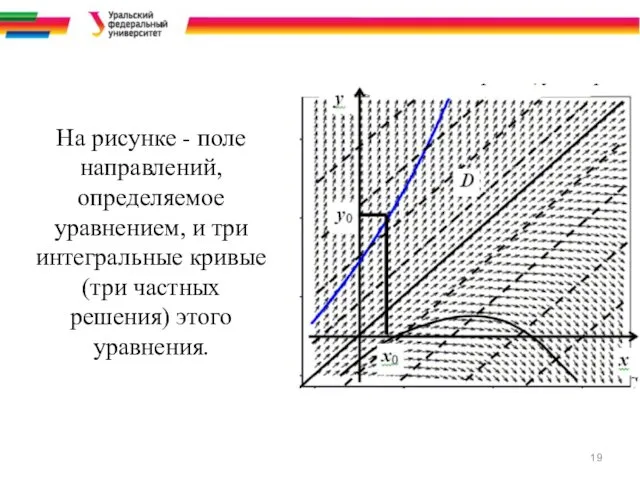
- 19. На рисунке - поле направлений, определяемое уравнением, и три интегральные кривые (три частных решения) этого уравнения.
- 20. Метод изоклин. Для изображения поля направлений, задаваемого дифференциальным уравнением, рассматривают линии уровня функции f(x, y), т.е.
- 21. Метод изоклин. Изоклины – линии с уравнением
- 23. Скачать презентацию















 Письмо по электронной почте от микроба Лентяйкина
Письмо по электронной почте от микроба Лентяйкина ГИА. Вопрос А3. Химическая связь
ГИА. Вопрос А3. Химическая связь Открытые переломы, гнойные осложнения переломов, травматический остеомиелит, современные методы лечения открытых переломов
Открытые переломы, гнойные осложнения переломов, травматический остеомиелит, современные методы лечения открытых переломов Тайны яблока
Тайны яблока Анализ ликвидности и платежеспособности организации на основе бухгалтерской отчетности на примере ООО Вертикаль
Анализ ликвидности и платежеспособности организации на основе бухгалтерской отчетности на примере ООО Вертикаль Программа работы с одаренными детьми
Программа работы с одаренными детьми методическая разработка интегрированного урока по предмету Численные методы и Основы алгоритмизации и программирования
методическая разработка интегрированного урока по предмету Численные методы и Основы алгоритмизации и программирования 20240123_izo_5_klass._tema_6._konstruktsiya_i_dekor_predmetov_narodnogo_byta
20240123_izo_5_klass._tema_6._konstruktsiya_i_dekor_predmetov_narodnogo_byta лекция_Растворы
лекция_Растворы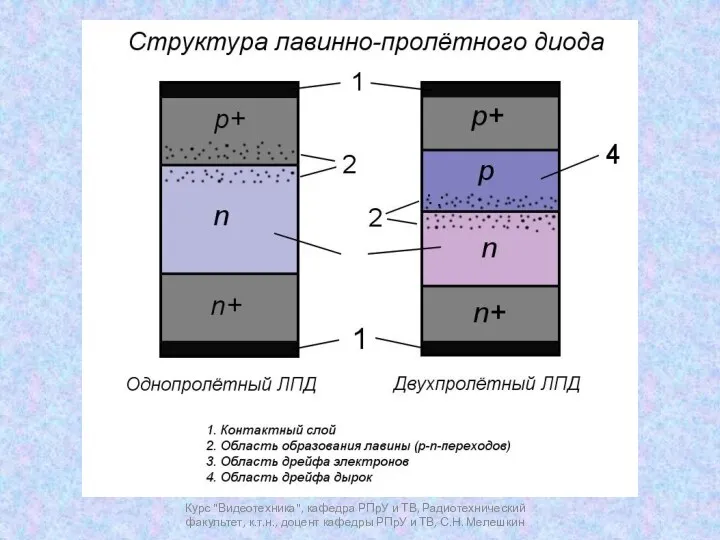 Лавинно-пролётный диод. Диод Ганна
Лавинно-пролётный диод. Диод Ганна Кубические и биквадратные уравнения
Кубические и биквадратные уравнения Источники трудового права
Источники трудового права Артикуляционная гимнастика с обезьянкой Соней
Артикуляционная гимнастика с обезьянкой Соней Презентация Покормите птиц зимой
Презентация Покормите птиц зимой Геометрические фигуры (для дошкольников)
Геометрические фигуры (для дошкольников) Химия. Образовательные программы магистратуры
Химия. Образовательные программы магистратуры Тұрақты стенокардия
Тұрақты стенокардия Введение во храм Пресвятой Богородицы
Введение во храм Пресвятой Богородицы Использование нетрадиционной техники на занятиях Юный художник
Использование нетрадиционной техники на занятиях Юный художник Рекламная кампания. Планирование и организация
Рекламная кампания. Планирование и организация Буквенная запись свойств сложения и вычитания
Буквенная запись свойств сложения и вычитания Карстовые процессы
Карстовые процессы Девиантное поведение детей и подростков – виды, причины, феноменология
Девиантное поведение детей и подростков – виды, причины, феноменология Инфологическое моделирование
Инфологическое моделирование Недостаточность коры надпочечников
Недостаточность коры надпочечников Потребитель и его права
Потребитель и его права Динамическое проектирование систем стабилизации летательных аппаратов. Исполнительные устройства. Рулевой привод
Динамическое проектирование систем стабилизации летательных аппаратов. Исполнительные устройства. Рулевой привод В здоровом теле - здоровый дух
В здоровом теле - здоровый дух