Содержание
- 2. Готфрид Фридрих Лейбниц 1646 - 1716 Иоган Бернулли 1667 - 1748 Якоб Бернулли 1654 - 1705
- 3. ОПРЕДЕЛЕНИЕ 1. Пусть X и Y – числовые множества. Если задано правило, по которому каждому элементу
- 4. Способы задания функции: аналитический графический табличный Аналитический способ. Функция задается формулой, которая указывает последовательность операций, которые
- 5. Примеры :
- 6. При аналитическом способе задания ( в случае, если область Определения не указана явно) область определения функции
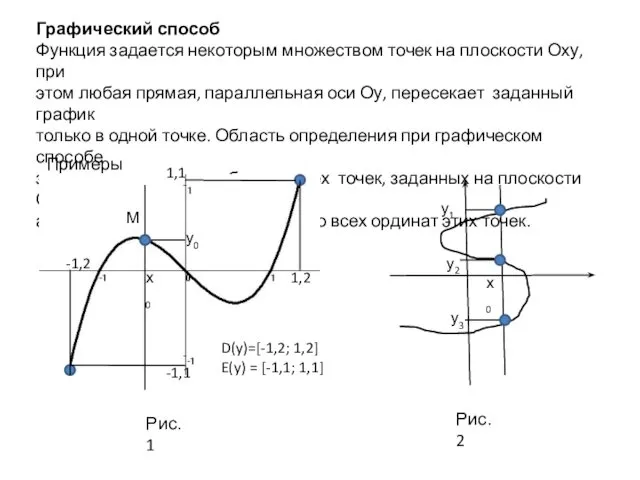
- 7. Графический способ Функция задается некоторым множеством точек на плоскости Оху, при этом любая прямая, параллельная оси
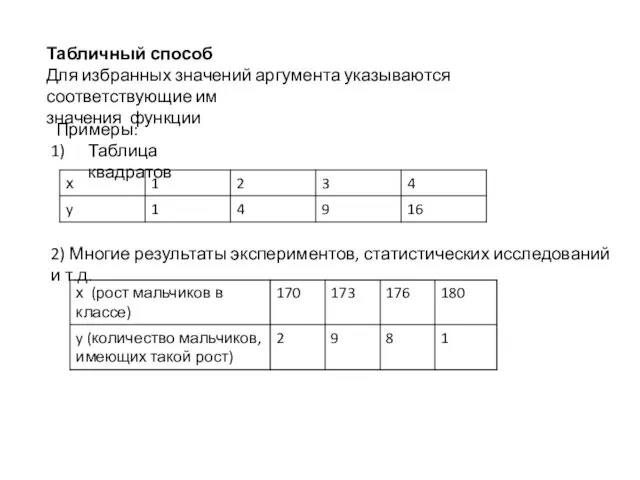
- 8. Табличный способ Для избранных значений аргумента указываются соответствующие им значения функции Примеры: Таблица квадратов 2) Многие
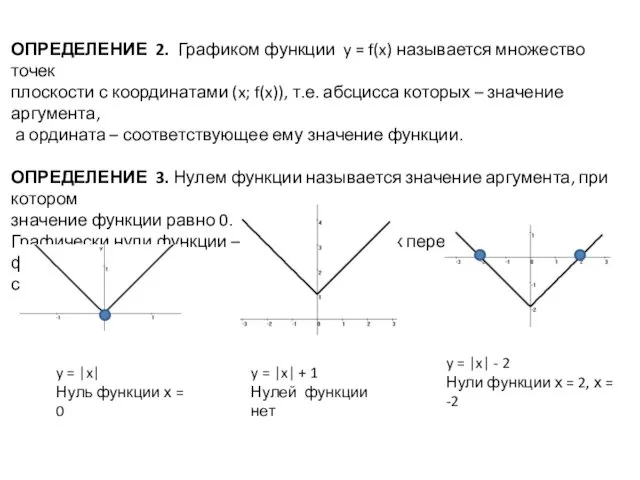
- 9. ОПРЕДЕЛЕНИЕ 2. Графиком функции y = f(x) называется множество точек плоскости с координатами (x; f(x)), т.е.
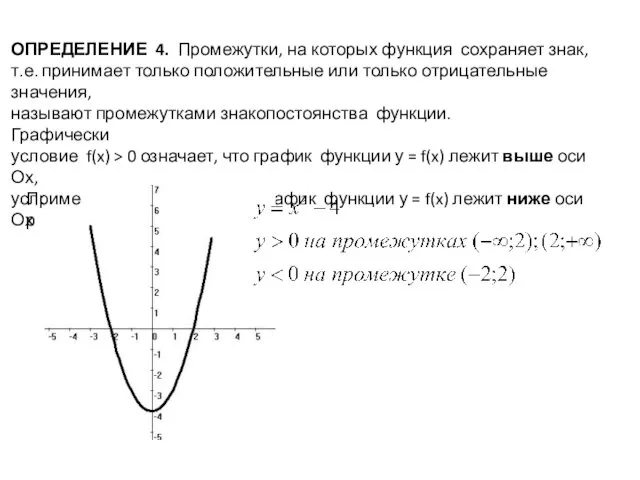
- 10. ОПРЕДЕЛЕНИЕ 4. Промежутки, на которых функция сохраняет знак, т.е. принимает только положительные или только отрицательные значения,
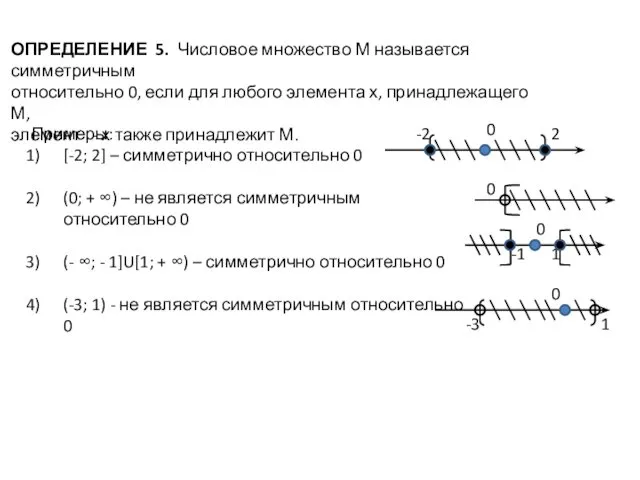
- 11. ОПРЕДЕЛЕНИЕ 5. Числовое множество М называется симметричным относительно 0, если для любого элемента х, принадлежащего М,
- 12. ОПРЕДЕЛЕНИЕ 6. Функция y = f(x) называется четной, если ее область определения симметрична относительно 0 и
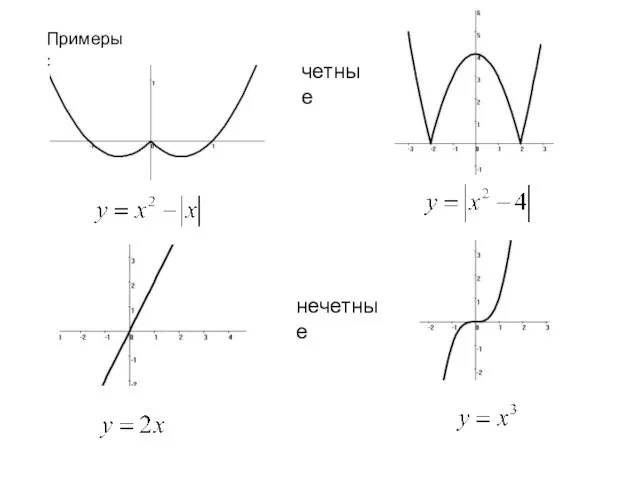
- 13. Примеры: четные нечетные
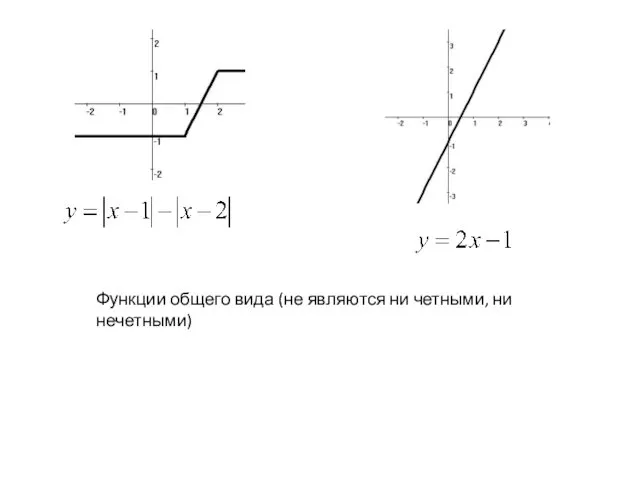
- 14. Функции общего вида (не являются ни четными, ни нечетными)
- 15. ОПРЕДЕЛЕНИЕ 7. Функция y = f(x) называется возрастающей на промежутке Р, принадлежащим области определения функции, если
- 16. Примеры: 1. возрастающие функции 2. убывающая функция Замечание. Нельзя считать функцию y = k/x возрастающей или
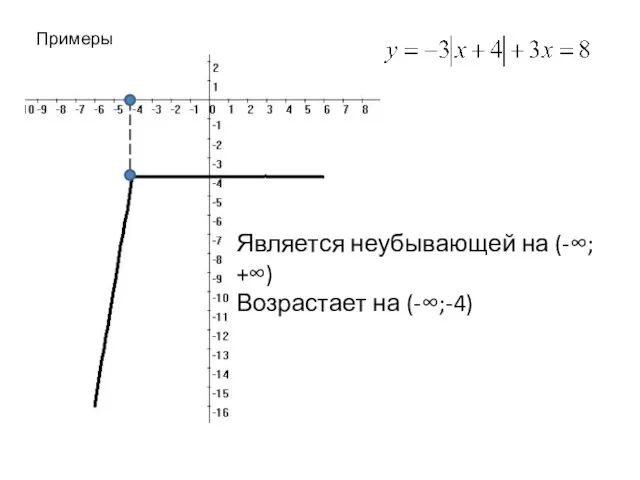
- 17. Примеры: Является неубывающей на (-∞; +∞) Возрастает на (-∞;-4)
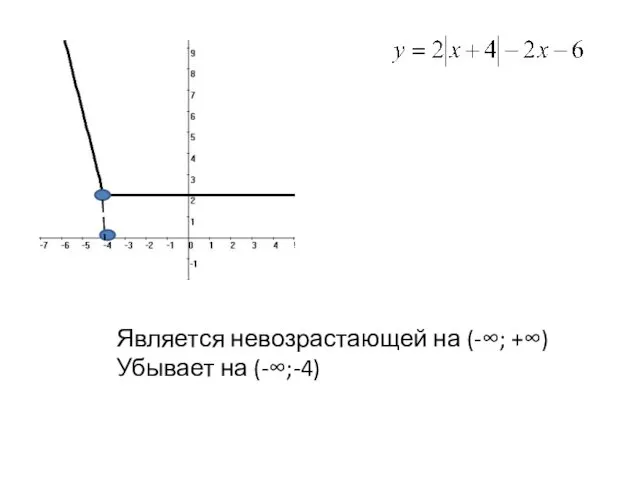
- 18. Является невозрастающей на (-∞; +∞) Убывает на (-∞;-4)
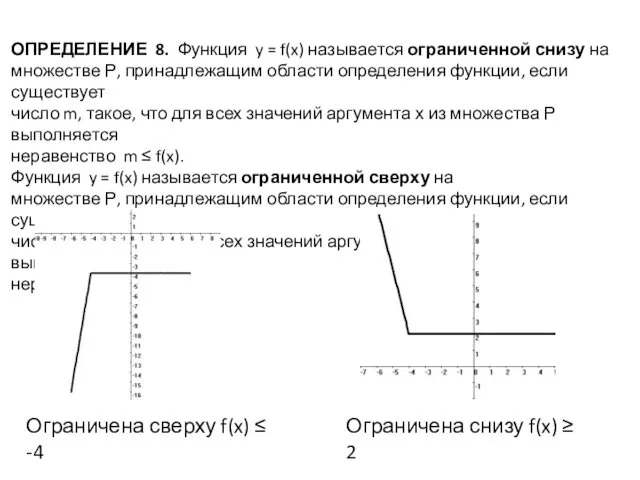
- 19. ОПРЕДЕЛЕНИЕ 8. Функция y = f(x) называется ограниченной снизу на множестве Р, принадлежащим области определения функции,
- 20. ОПРЕДЕЛЕНИЕ 9. Наименьшее из всех значений, которые может принимать переменная у (если такое существует) называется наименьшим
- 21. ОПРЕДЕЛЕНИЕ 9. Функция вида y = кх + b, где k и b – действительные числа,
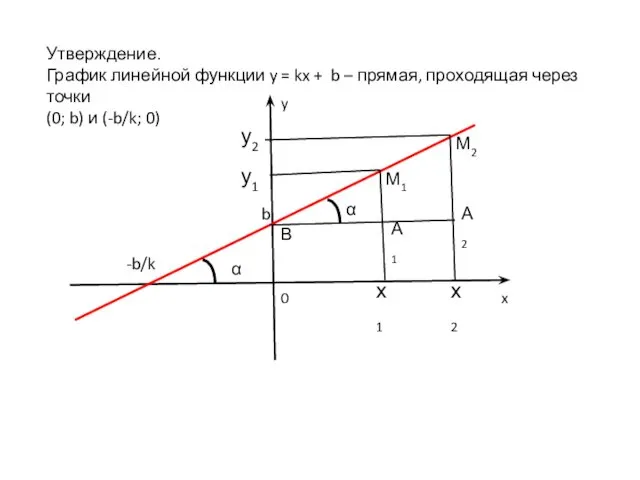
- 22. Утверждение. График линейной функции y = kx + b – прямая, проходящая через точки (0; b)
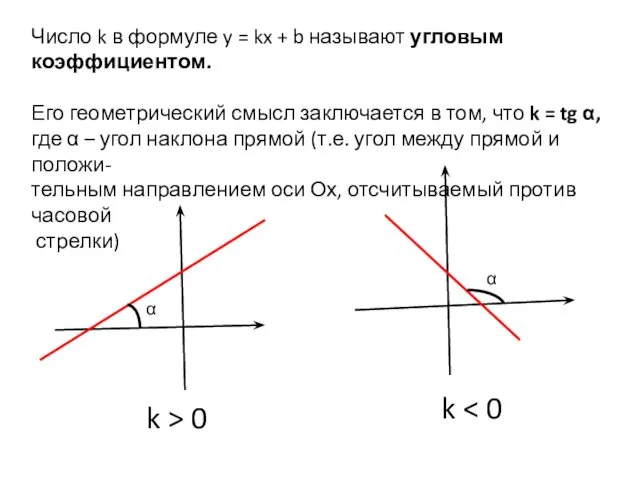
- 23. Число k в формуле y = kx + b называют угловым коэффициентом. Его геометрический смысл заключается
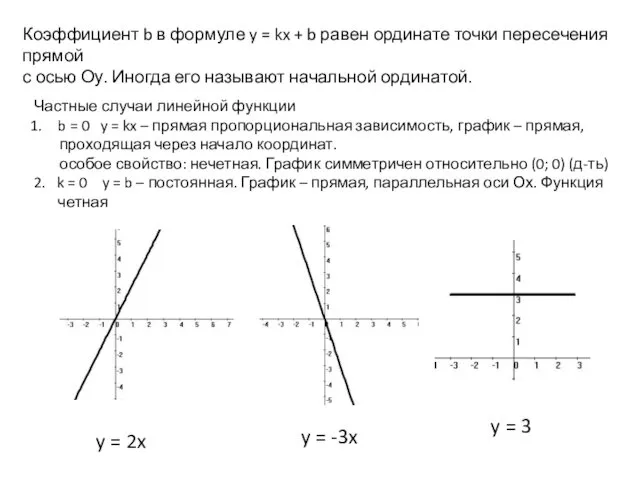
- 24. Коэффициент b в формуле y = kx + b равен ординате точки пересечения прямой с осью
- 25. ОПРЕДЕЛЕНИЕ 9. Функция вида y = ах2 + bх + с, где а, b и с
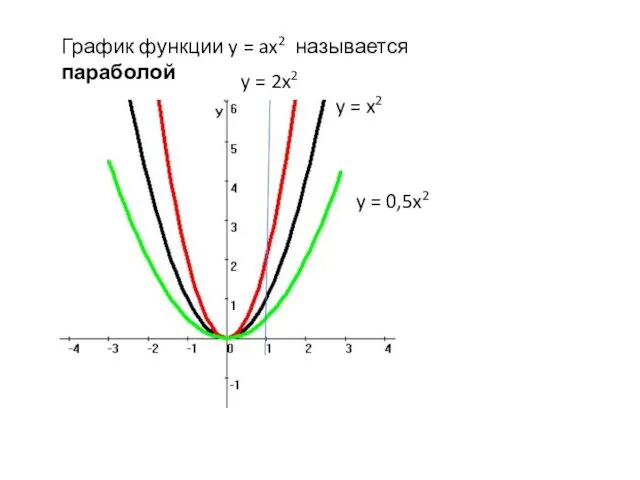
- 26. График функции y = ax2 называется параболой y = x2 y = 2x2 y = 0,5x2
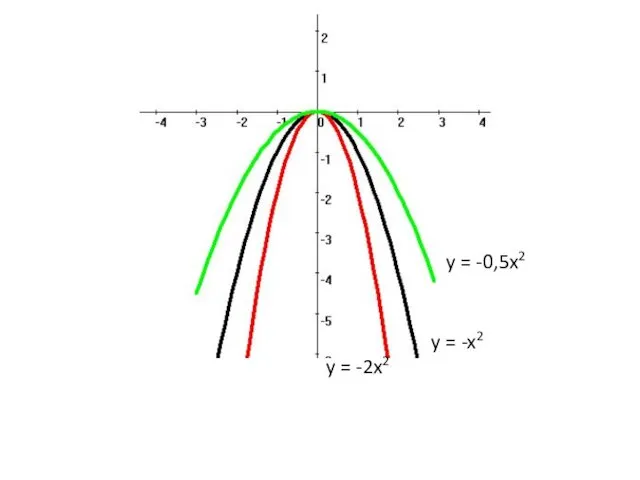
- 27. y = -2x2 y = -0,5x2 y = -x2
- 29. Скачать презентацию



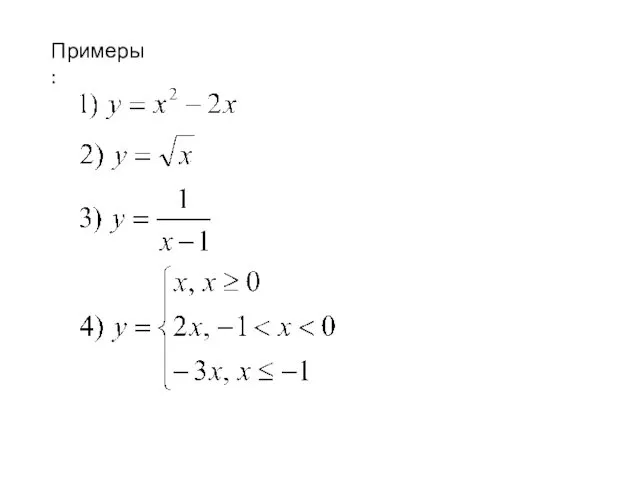







 Научно-техническая революция
Научно-техническая революция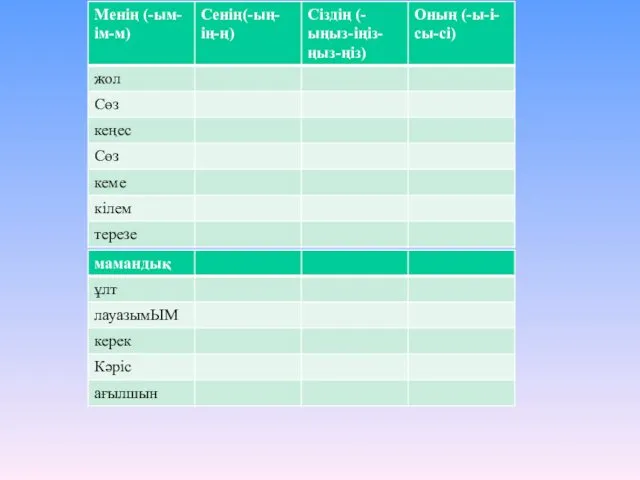 Өзіміз туралы айтайық
Өзіміз туралы айтайық Устройство ЭВМ
Устройство ЭВМ Мы живём среди друзей
Мы живём среди друзей Каучук и резина. История открытия каучука
Каучук и резина. История открытия каучука Презентация проекта Предновогодний календарь
Презентация проекта Предновогодний календарь Команда развития грихастха-ашрама
Команда развития грихастха-ашрама фотоколлаж Бородино
фотоколлаж Бородино Химия глин и принципы ингибирования глинистых пород
Химия глин и принципы ингибирования глинистых пород Влияние цвета на здоровье человека
Влияние цвета на здоровье человека Оформление групповой комнаты
Оформление групповой комнаты Алгоритм составления социального проекта
Алгоритм составления социального проекта Канальная вентиляция. Канальное вентиляционное оборудование Даичи
Канальная вентиляция. Канальное вентиляционное оборудование Даичи Урок химии в 10 классе по теме Белки как биополимеры
Урок химии в 10 классе по теме Белки как биополимеры Подснежники
Подснежники Классный час Огонь - друг и враг человека
Классный час Огонь - друг и враг человека Скороговорки
Скороговорки Римский клуб
Римский клуб Тепловое оборудование в гостиницах и ресторанах
Тепловое оборудование в гостиницах и ресторанах Северная Европа во времена викингов
Северная Европа во времена викингов Презентация к уроку Семья - важнейший институт духовно-нравственного развития
Презентация к уроку Семья - важнейший институт духовно-нравственного развития Рекомендации по содержанию презентации
Рекомендации по содержанию презентации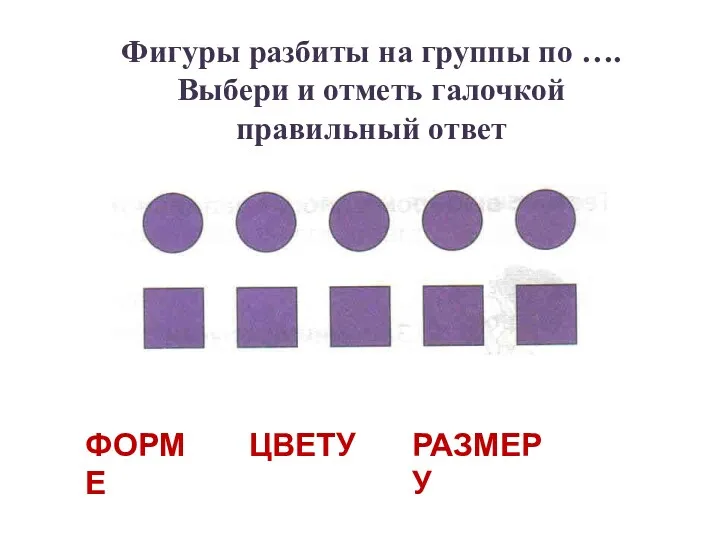 Презентация к занятию на тему: Классификация предметов по форме, цвету, размеру
Презентация к занятию на тему: Классификация предметов по форме, цвету, размеру Революции в 1848-1849 годы, в Европе
Революции в 1848-1849 годы, в Европе Зарубежный опыт применения аудита эффективности
Зарубежный опыт применения аудита эффективности Публикации учащихся: Проект по ОДНК на тему: Свадебные обряды в буддизме
Публикации учащихся: Проект по ОДНК на тему: Свадебные обряды в буддизме Избирательная реформа и демократизация Великобритании в XIX веке
Избирательная реформа и демократизация Великобритании в XIX веке презентация
презентация