Содержание
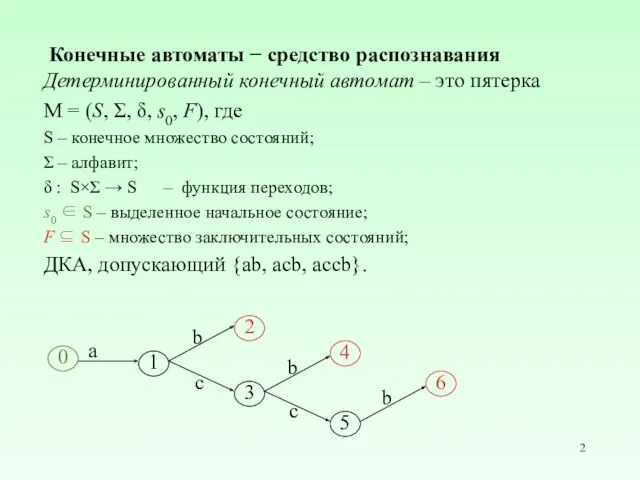
- 2. Конечные автоматы − средство распознавания Детерминированный конечный автомат – это пятерка M = (S, Σ, δ,
- 3. Формальные последовательности Последовательность Туэ - Морса Способы задания 1. Итерации морфизмов. Σ = {a1…aq} ϕ :
- 4. Формальные последовательности Чи́сла Фибона́ччи — 0, 1, 1, 2, 3, 5, 8, 13, 21, 34, 55,
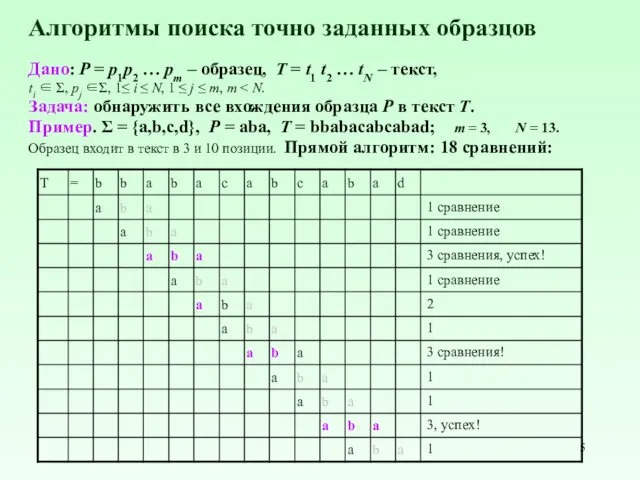
- 5. Алгоритмы поиска точно заданных образцов Дано: P = p1p2 … pm – образец, T = t1
- 6. Алгоритм Кнута-Морриса-Пратта Здесь ti+1… ti+j = p1… pj, но ti+j+1 ≠ pj+1. Если максимальный суффикс цепочки
- 7. Алгоритм Кнута-Морриса-Пратта Функция переходов: g(j − 1, pj) = j, j =1…m; g(0,a)=0 для всех a
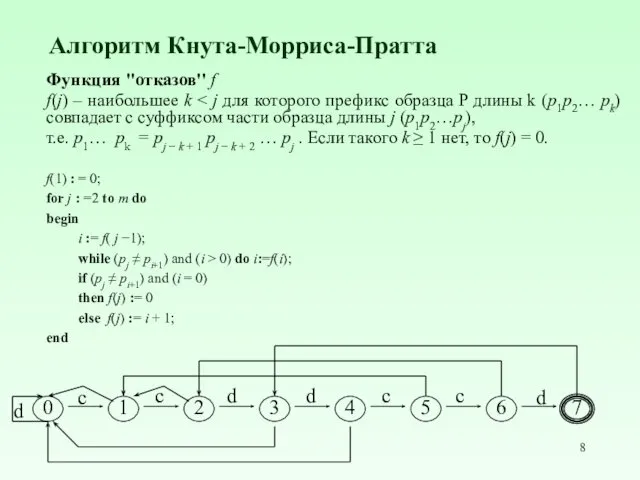
- 8. Алгоритм Кнута-Морриса-Пратта Функция "отказов'' f f(j) – наибольшее k т.е. p1… pk = pj − k
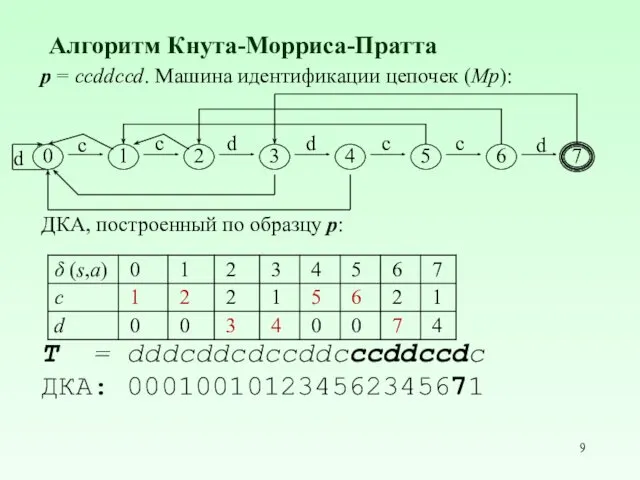
- 9. Алгоритм Кнута-Морриса-Пратта p = ccddccd. Машина идентификации цепочек (Mp): ДКА, построенный по образцу p: T =
- 10. Алгоритм Бойера-Мура Cравнение символов – справа налево !!! 1. Правило «плохого символа». P 1 1 m
- 11. Алгоритм Бойера-Мура 1. Правило «плохого символа». P 1 1 m i+1 i+m T T P P
- 12. Алгоритм Бойера-Мура 2. Правило «хорошего cуффикса». P 1 1 m i+1 i+m T P y x
- 13. Алгоритм Shift-And Пример. Пусть Σ = {a,b,c}, p=aabac, T=aabaacaabacab. R[m, j] = 1: P в (j
- 14. Алгоритм Shift-And Пример. Пусть Σ = {a,b,c}, p=aabac, T=aabaacaabacab. Схема перехода от j-го столбца R к
- 15. Алгоритм Shift-And Пример. Пусть Σ = {a,b,c}, p=aabac, T=aabaacaabacab. Схема перехода от 3-го столбца R к
- 16. Алгоритм Карпа-Рабина ns : Σ → [1.. |Σ|] - порядок символов в Σ. Пусть s =
- 17. Обобщения задачи поиска образца: Поиск образца, позиции которого заданы множествами символов A- [AG]-C-[CG]-¬T-x-A (AGCCAAA, AACCGCA…) Поиск
- 18. Алгоритм Ахо-Корасик Задача. Задано множество образцов P = {P1, P2, … Pz}. Требуется обнаружить все вхождения
- 19. Алгоритм Ахо-Корасик Этап предобработки: построение ДКА по исходному множеству образцов Этап поиска: однократный "прогон" текста через
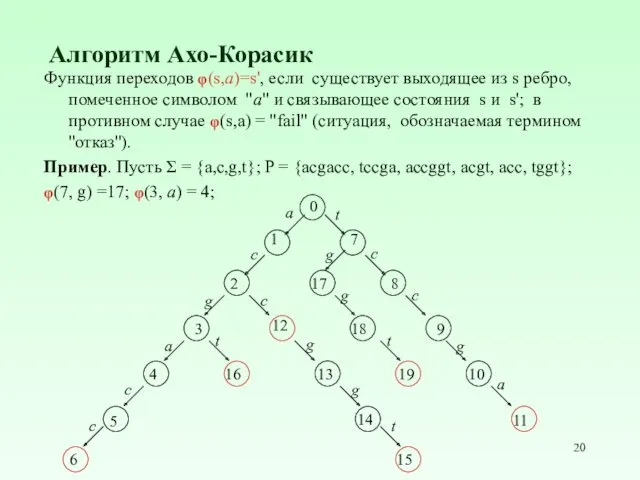
- 20. Алгоритм Ахо-Корасик Функция переходов φ(s,a)=s', если существует выходящее из s ребро, помеченное символом "a" и связывающее
- 22. Скачать презентацию










![Алгоритм Карпа-Рабина ns : Σ → [1.. |Σ|] - порядок](/_ipx/f_webp&q_80&fit_contain&s_1440x1080/imagesDir/jpg/45834/slide-15.jpg)



 Санкт -Петербург
Санкт -Петербург Задачи на совместную работу
Задачи на совместную работу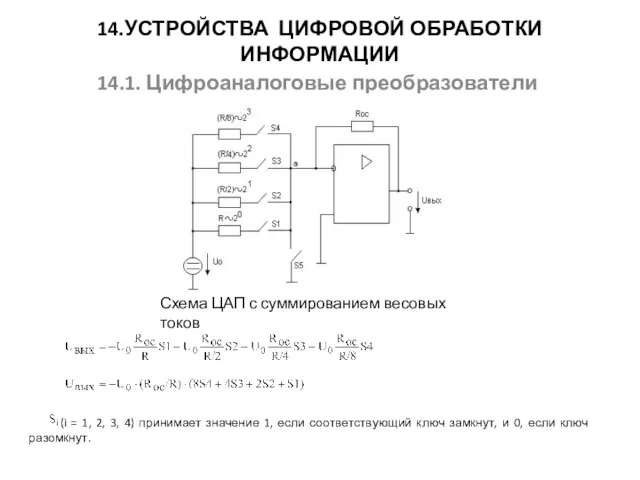 Устройства цифровой обработки информации
Устройства цифровой обработки информации Комплект радіостанції Becker RT6201/RCU6201 на вертольоті та його разміщення
Комплект радіостанції Becker RT6201/RCU6201 на вертольоті та його разміщення Презентации к курсу Химия и питание
Презентации к курсу Химия и питание Предмет, цели и задачи товароведения
Предмет, цели и задачи товароведения М. Зощенко. Золотые слова
М. Зощенко. Золотые слова Разнообразие животных
Разнообразие животных Web-программирование. Лекция 7. HTTP. Django
Web-программирование. Лекция 7. HTTP. Django Афинские школы
Афинские школы Русская наука во второй половине XIX века
Русская наука во второй половине XIX века Создание промышленных предприятий по производству органоминеральных удобрений из осадков сточных вод
Создание промышленных предприятий по производству органоминеральных удобрений из осадков сточных вод Изобразительное творчество дошкольников с точки зрения психологии
Изобразительное творчество дошкольников с точки зрения психологии Профессия – родину защищать
Профессия – родину защищать Тундра
Тундра Мұнай - көмірсутектер қоспасы болып табылатын, жанатын майлы сұйықтық, пайдалы қазбалардың ең маңызды түрі
Мұнай - көмірсутектер қоспасы болып табылатын, жанатын майлы сұйықтық, пайдалы қазбалардың ең маңызды түрі Шляпный этикет, как правильно вписать аксессуар из прошлого в современный образ
Шляпный этикет, как правильно вписать аксессуар из прошлого в современный образ Сутність маркетингу та його сучасна концепція
Сутність маркетингу та його сучасна концепція Психология развития и возрастная психология
Психология развития и возрастная психология Северная война (1700-1721)
Северная война (1700-1721) Природные ресурсы Западно-Сибирской равнины и условия их освоения.
Природные ресурсы Западно-Сибирской равнины и условия их освоения. Устройство шестивесельного яла
Устройство шестивесельного яла Тредмил-тест. Метод функциональной диагностики заболев аний сердечнососудистой системы
Тредмил-тест. Метод функциональной диагностики заболев аний сердечнососудистой системы Чего себе не хочешь, того другим не делай.
Чего себе не хочешь, того другим не делай. Single screw compressor presentation. Working principle & inspection guidelines
Single screw compressor presentation. Working principle & inspection guidelines Фонарик из цветной бумаги и картона
Фонарик из цветной бумаги и картона Эксплуатация нефтяных и газовых скважин. Методы увеличения дебита скважин
Эксплуатация нефтяных и газовых скважин. Методы увеличения дебита скважин Предохранители. Виды предохранителей
Предохранители. Виды предохранителей