Решение заданий 14 (С2) по материалам ЕГЭ профильного уровня (нахождение углов, расстояний, построение сечений) презентация
Содержание
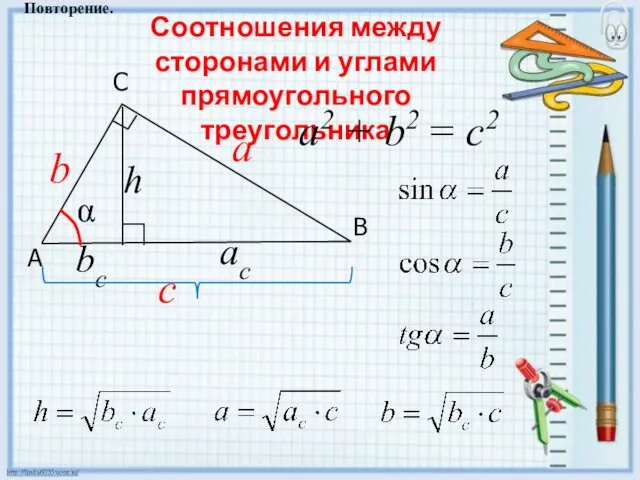
- 2. Соотношения между сторонами и углами прямоугольного треугольника Повторение. C A В a2 + b2 = c2
- 3. a2 = B a A C c b Квадрат стороны треугольника равен сумме квадратов двух других
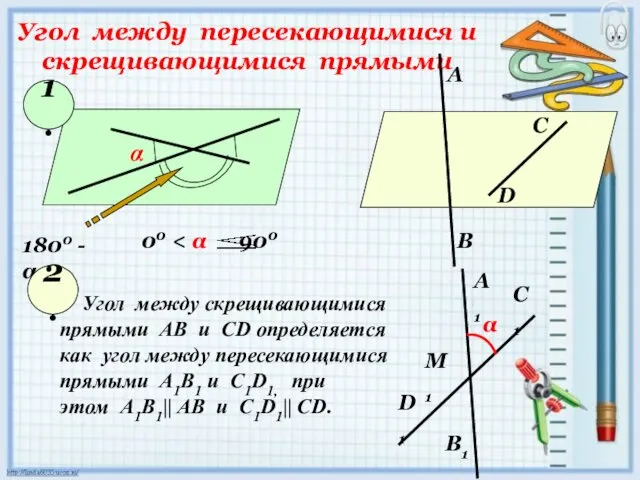
- 4. Угол между пересекающимися и скрещивающимися прямыми α 1800 - α 00 1. 2. Угол между скрещивающимися
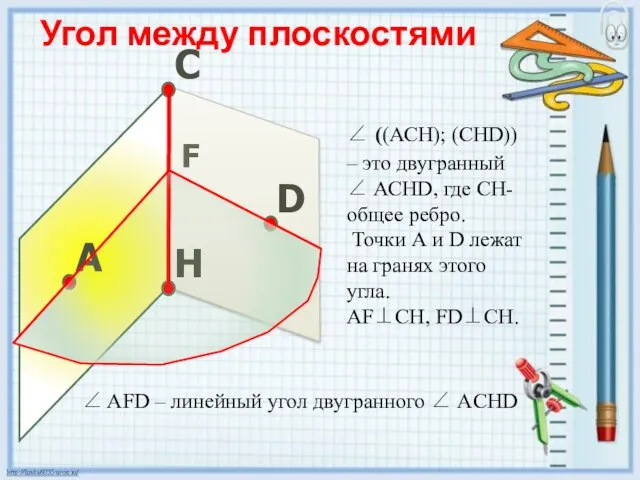
- 5. ∠ ((АСН); (СНD)) – это двугранный ∠ АСНD, где СН-общее ребро. Точки А и D лежат
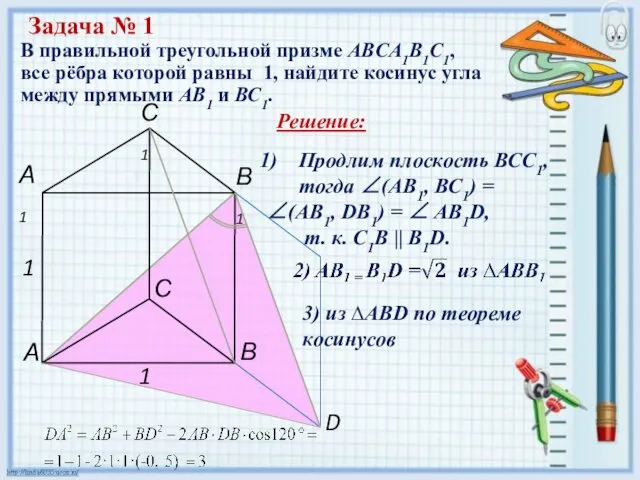
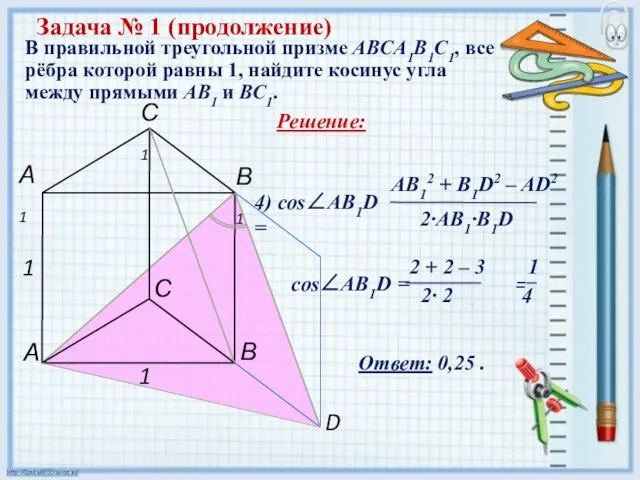
- 6. В правильной треугольной призме ABCA1B1C1, все рёбра которой равны 1, найдите косинус угла между прямыми АВ1
- 7. В правильной треугольной призме ABCA1B1C1, все рёбра которой равны 1, найдите косинус угла между прямыми АВ1
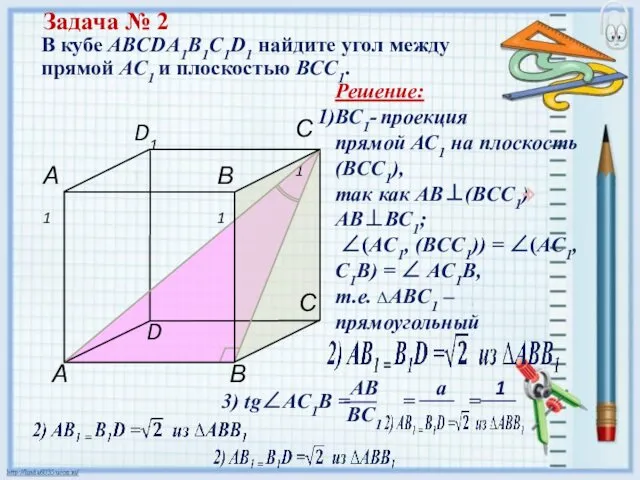
- 8. В кубе ABCDA1B1C1D1 найдите угол между прямой AC1 и плоскостью ВСC1. Задача № 2 С В
- 9. Основанием прямой треугольной призмы ABCA1B1C1, является равнобедренный треугольник АВС, в котором АВ = ВС = 20,
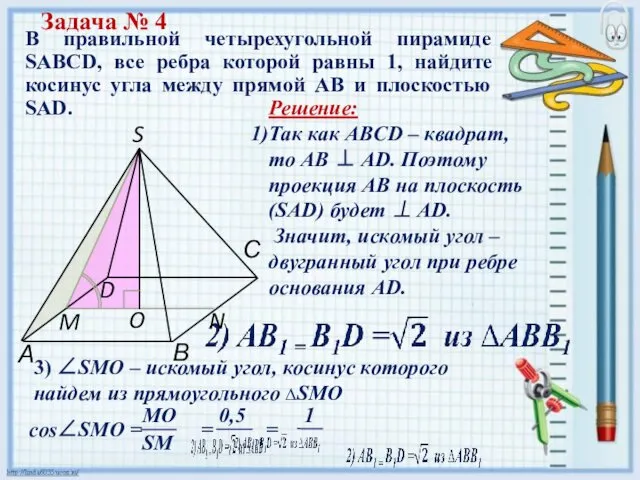
- 10. Решение: Так как ABCD – квадрат, то АВ ⊥ AD. Поэтому проекция AB на плоскость (SAD)
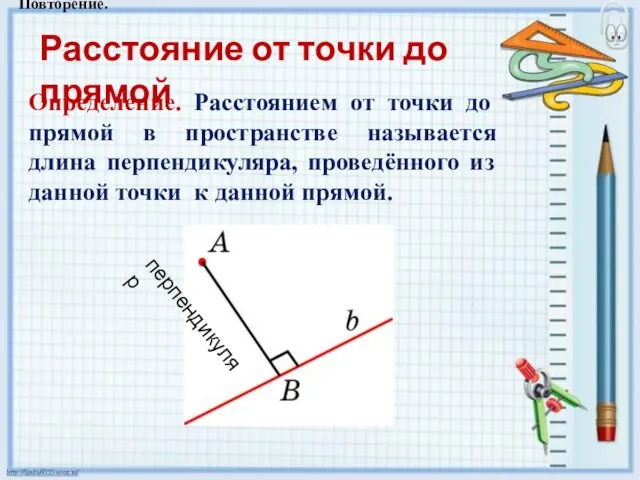
- 11. Расстояние от точки до прямой Определение. Расстоянием от точки до прямой в пространстве называется длина перпендикуляра,
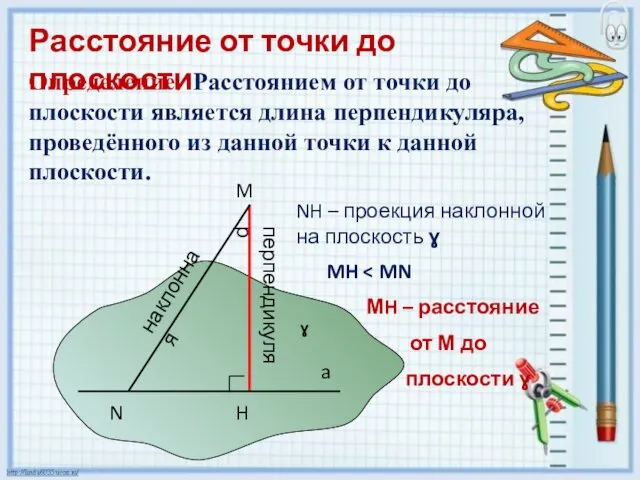
- 12. Расстояние от точки до плоскости Определение. Расстоянием от точки до плоскости является длина перпендикуляра, проведённого из
- 13. Общим перпендикуляром двух скрещивающихся прямых называют отрезок с концами на этих прямых, являющийся перпендикуляром к каждой
- 14. Способы вычисления расстояния между скрещивающимися прямыми Расстояние между скрещивающимися прямыми равно расстоянию от любой точки одной
- 15. Способы вычисления расстояния между скрещивающимися прямыми Расстояние между скрещивающимися прямыми равно расстоянию между двумя параллельными плоскостями,
- 16. Способы вычисления расстояния между скрещивающимися прямыми Расстояние между скрещивающимися прямыми равно расстоянию между их проекциями на
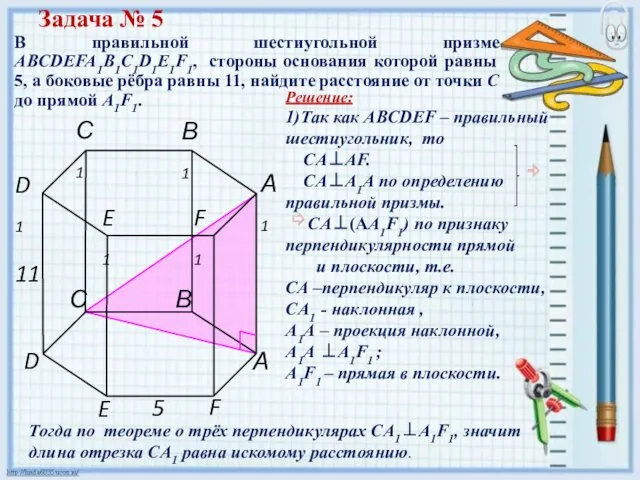
- 17. В правильной шестиугольной призме ABCDEFA1B1C1D1E1F1, стороны основания которой равны 5, а боковые рёбра равны 11, найдите
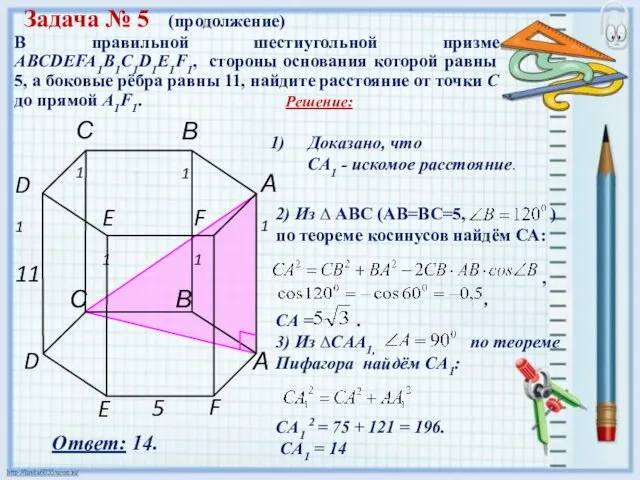
- 18. В правильной шестиугольной призме ABCDEFA1B1C1D1E1F1, стороны основания которой равны 5, а боковые рёбра равны 11, найдите
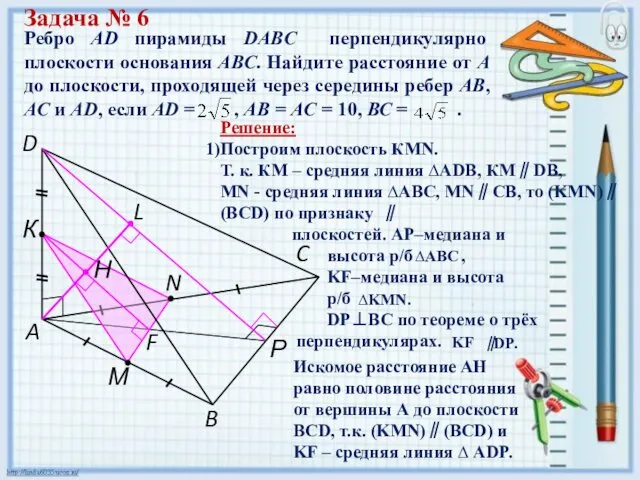
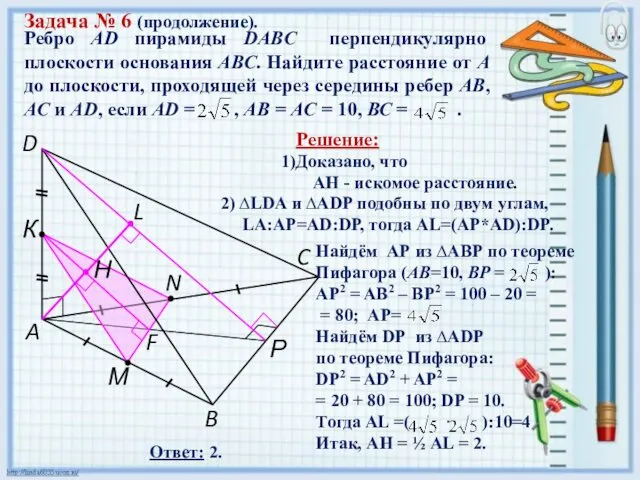
- 19. Ребро AD пирамиды DABC перпендикулярно плоскости основания АВС. Найдите расстояние от А до плоскости, проходящей через
- 20. Ребро AD пирамиды DABC перпендикулярно плоскости основания АВС. Найдите расстояние от А до плоскости, проходящей через
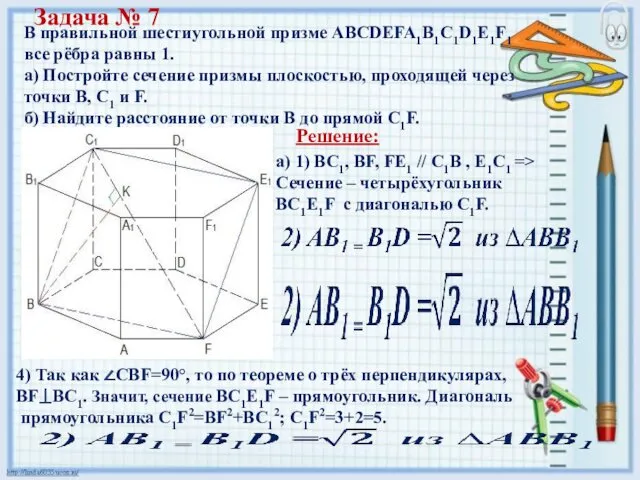
- 21. Задача № 7 В правильной шестиугольной призме АВCDEFA1B1C1D1E1F1 все рёбра равны 1. а) Постройте сечение призмы
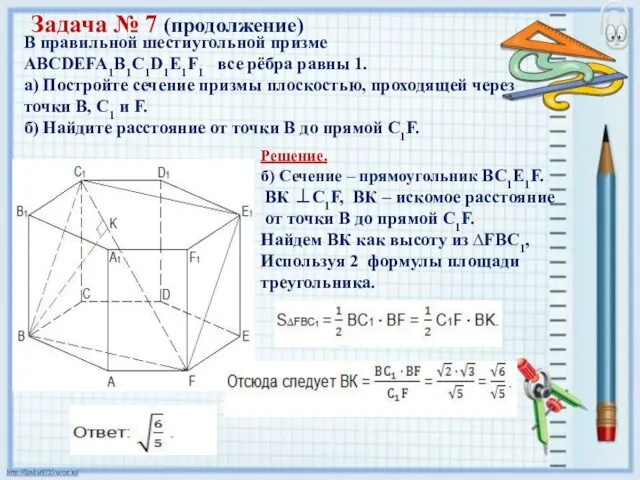
- 22. Задача № 7 (продолжение) Решение. б) Сечение – прямоугольник BC1E1F. ВК ⊥C1F, ВК – искомое расстояние
- 23. Задача №8 Основанием прямой четырехугольной призмы является квадрат ABCD со стороной , высота призмы равна .
- 24. Задача №8 (продолжение) Основанием прямой четырехугольной призмы ABCDA1B1C1D1 является квадрат ABCD со стороной , высота призмы
- 25. Задачи для самостоятельного решения На ребре AA1 прямоугольного параллелепипеда ABCDA1B1C1D1 взята точка E так, что A1E
- 26. Задачи для самостоятельного решения 3) В правильной шестиугольной призме А…F1 все рёбра равны 2. а) Докажите,
- 27. Задачи для самостоятельного решения 5) Высота правильной треугольной пирамиды равна 20, а медиана её основания равна
- 29. Скачать презентацию











 Системы впрыска бензина
Системы впрыска бензина Внеклассное мероприятие Расскажу тебе
Внеклассное мероприятие Расскажу тебе КапиталСтроиПроект. Жилом комплекс по ул. Карпова в Зареченском районе г. Тулы
КапиталСтроиПроект. Жилом комплекс по ул. Карпова в Зареченском районе г. Тулы Тайна имени Илья
Тайна имени Илья Економічне управління підприємством
Економічне управління підприємством Бурильная колонна
Бурильная колонна Литературный глобус С книгой вокруг света
Литературный глобус С книгой вокруг света Всероссийский конкурс для педагогов и учащихся Недаром помнит вся Россия, посвященный 200-летнему юбилею Отечественной войны
Всероссийский конкурс для педагогов и учащихся Недаром помнит вся Россия, посвященный 200-летнему юбилею Отечественной войны Измерение отрезков
Измерение отрезков Роторные Управляемые Системы Power Drive
Роторные Управляемые Системы Power Drive Врожденный нефротический синдром
Врожденный нефротический синдром Конспект и презентация для 1 класса День знаний
Конспект и презентация для 1 класса День знаний презентация Города-герои
презентация Города-герои Философия Новейшего времени и современности
Философия Новейшего времени и современности Центр безопасности Городок Светофорик
Центр безопасности Городок Светофорик Исчезающие виды птиц
Исчезающие виды птиц основы метода ассоциаций
основы метода ассоциаций Управление оборотным капиталом
Управление оборотным капиталом Агропромышленный комплекс. Лёгкая и пищевая промышленность
Агропромышленный комплекс. Лёгкая и пищевая промышленность Портфолио воспитателя детского сада Кирилловых Н. А.
Портфолио воспитателя детского сада Кирилловых Н. А. Презентация социального проекта к 65-летию Победы Следы войны под нашими крышами
Презентация социального проекта к 65-летию Победы Следы войны под нашими крышами Презентация к уроку краеведения Что такое краеведение.Я родился в Заполярье
Презентация к уроку краеведения Что такое краеведение.Я родился в Заполярье Выпускной - 2014
Выпускной - 2014 Организация сюжетно-ролевой игр в старшей группеБольница
Организация сюжетно-ролевой игр в старшей группеБольница Каскад колокольчиков
Каскад колокольчиков Пасхальная открытка
Пасхальная открытка Производные протопласта растительной клетки
Производные протопласта растительной клетки Омыртқа жотасының зақымдануы
Омыртқа жотасының зақымдануы