Содержание
- 2. История анализа сигналов В 19 веке, французский математик Жан Батист Жозеф Фурье показал, что любую функцию,
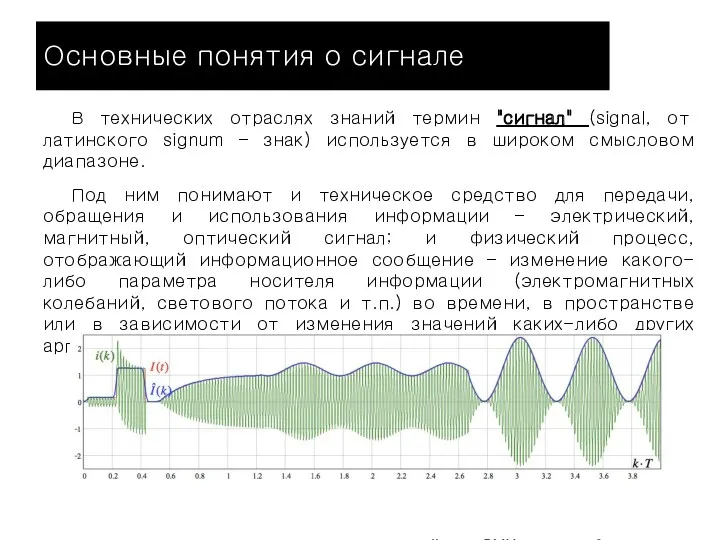
- 3. Основные понятия о сигнале В технических отраслях знаний термин "сигнал" (signal, от латинского signum – знак)
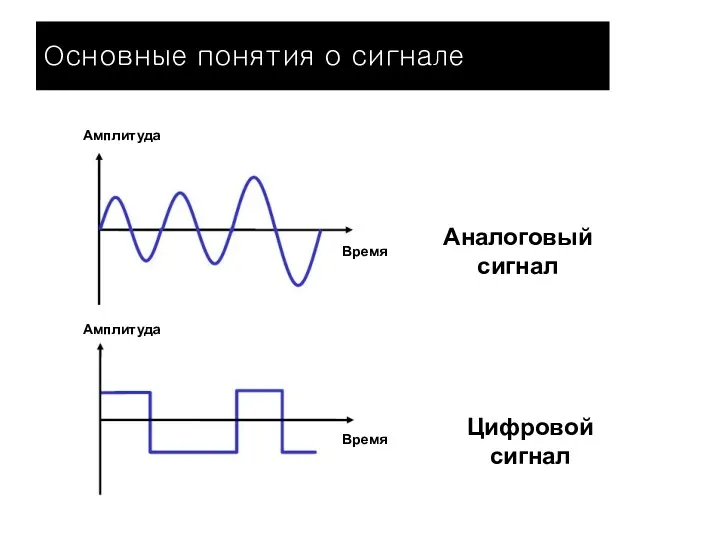
- 4. Аналоговый сигнал Цифровой сигнал Время Время Амплитуда Амплитуда Основные понятия о сигнале
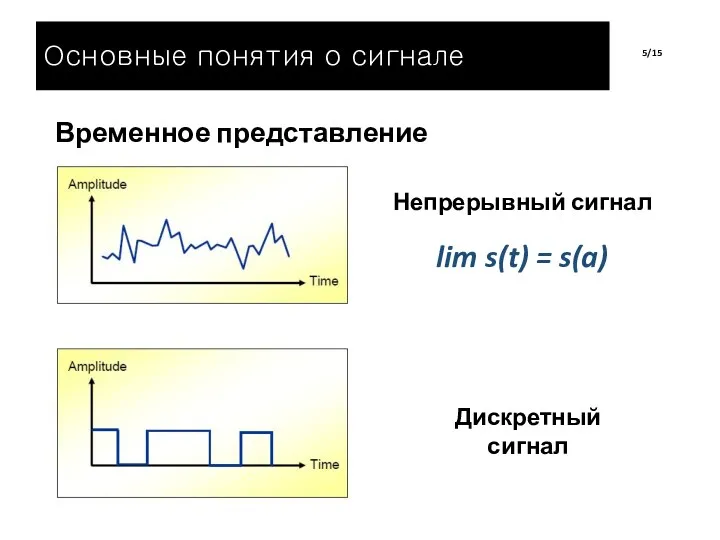
- 5. Временное представление /15 Непрерывный сигнал lim s(t) = s(a) Дискретный сигнал Основные понятия о сигнале
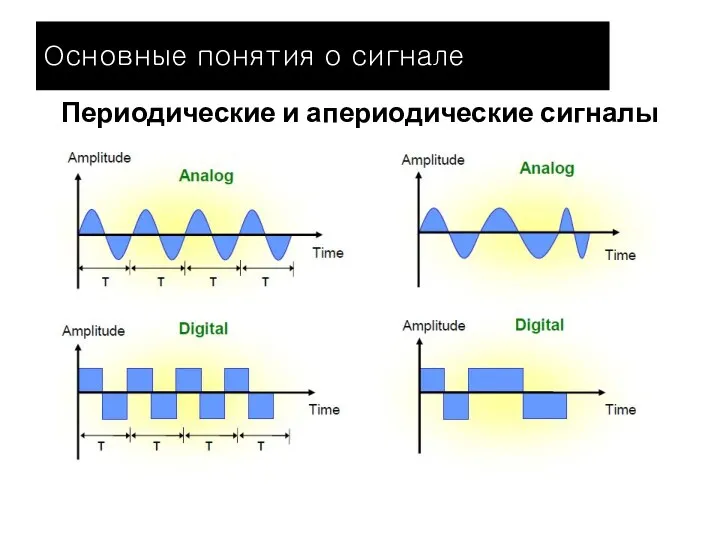
- 6. Периодические и апериодические сигналы Основные понятия о сигнале
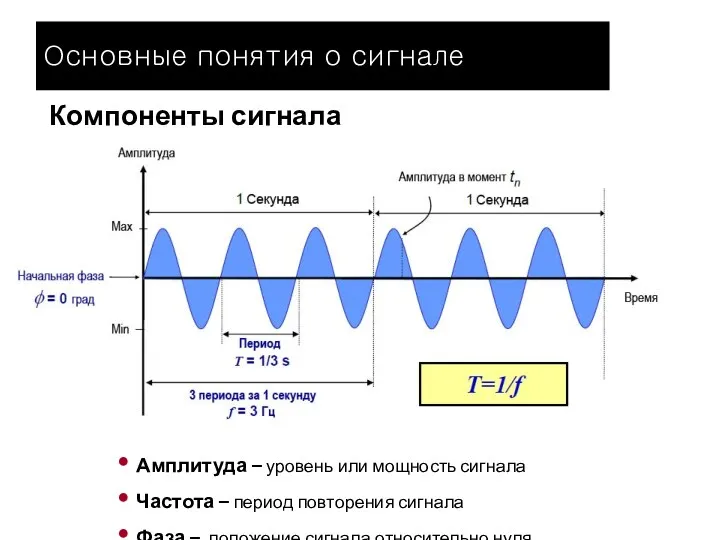
- 7. Компоненты сигнала Амплитуда – уровень или мощность сигнала Частота – период повторения сигнала Фаза – положение
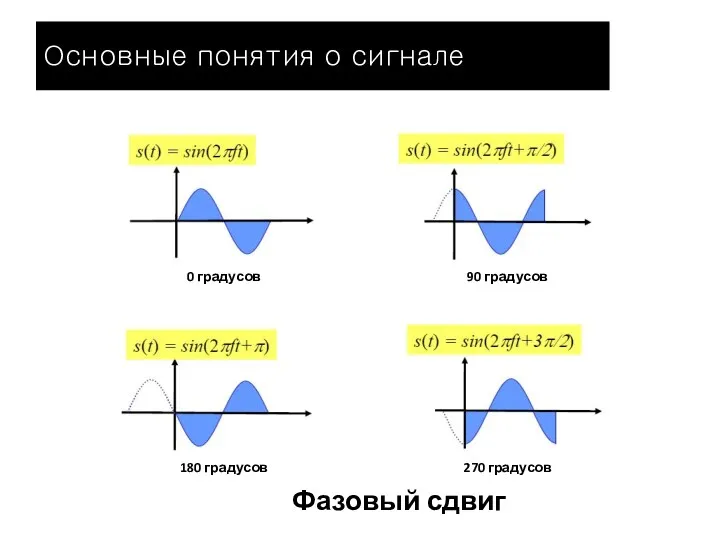
- 8. Фазовый сдвиг 90 градусов 270 градусов 0 градусов 180 градусов Основные понятия о сигнале
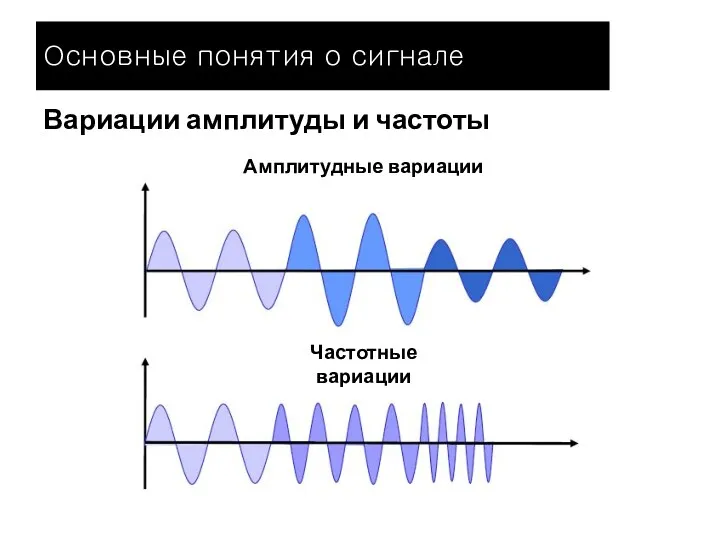
- 9. Вариации амплитуды и частоты Амплитудные вариации Частотные вариации Основные понятия о сигнале
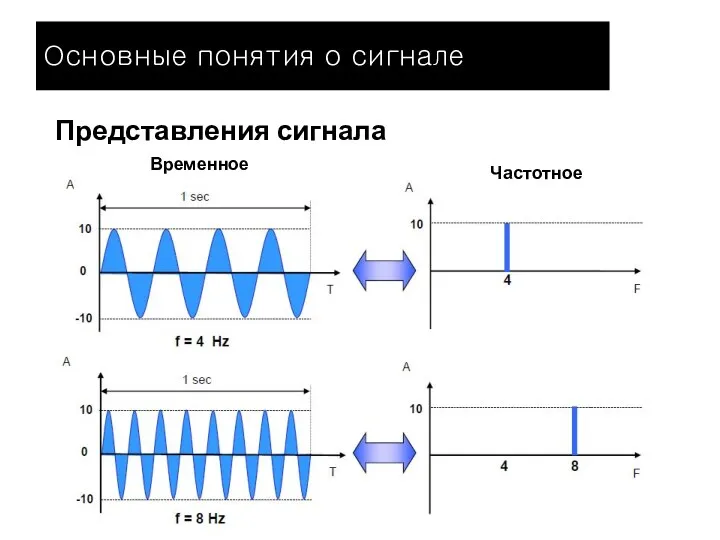
- 10. Представления сигнала Временное Частотное Основные понятия о сигнале
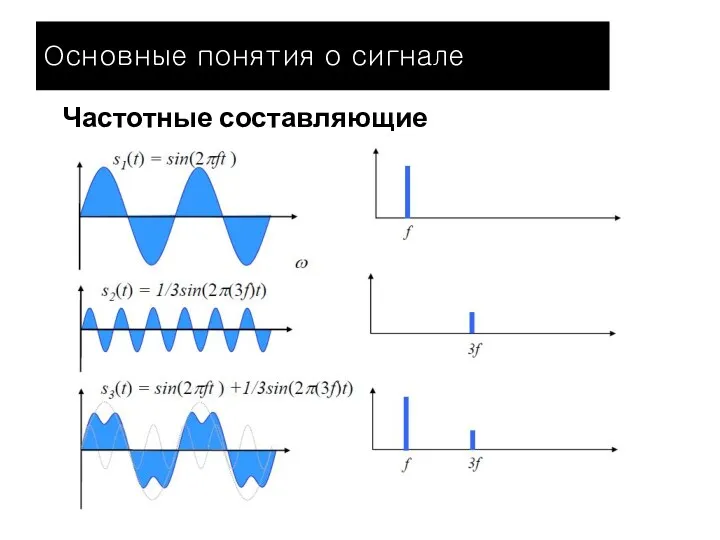
- 11. Частотные составляющие Основные понятия о сигнале
- 12. Основные понятия о сигнале Под "анализом" сигналов имеется в виду не только их чисто математические преобразования,
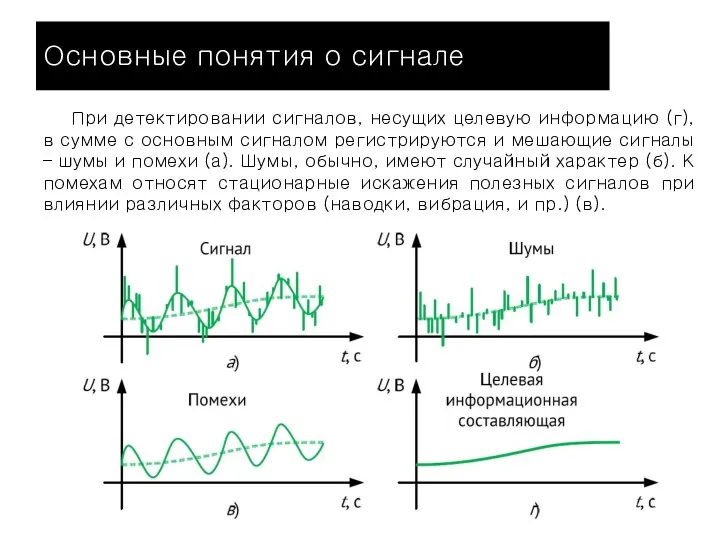
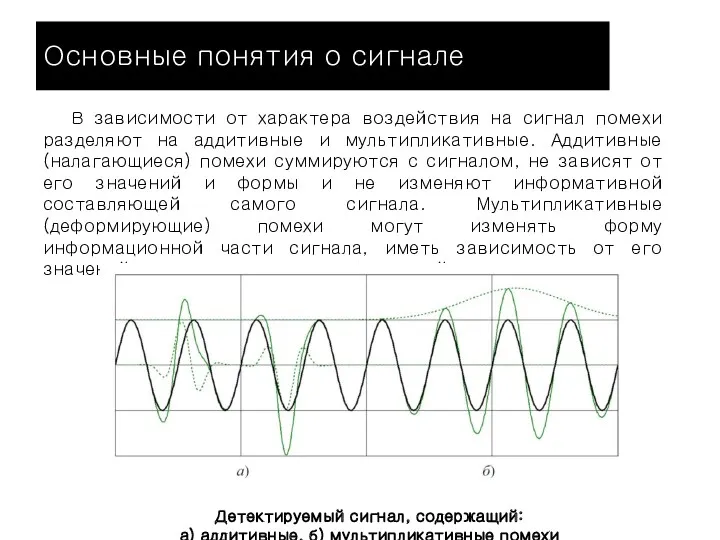
- 13. Основные понятия о сигнале При детектировании сигналов, несущих целевую информацию (г), в сумме с основным сигналом
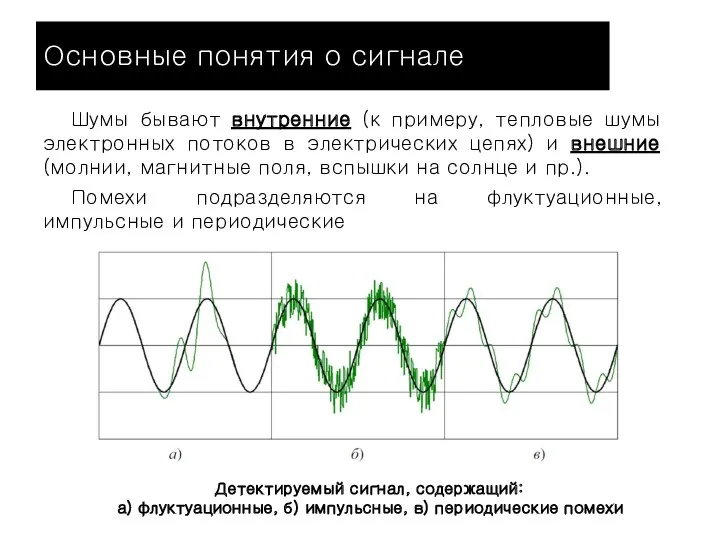
- 14. Основные понятия о сигнале Шумы бывают внутренние (к примеру, тепловые шумы электронных потоков в электрических цепях)
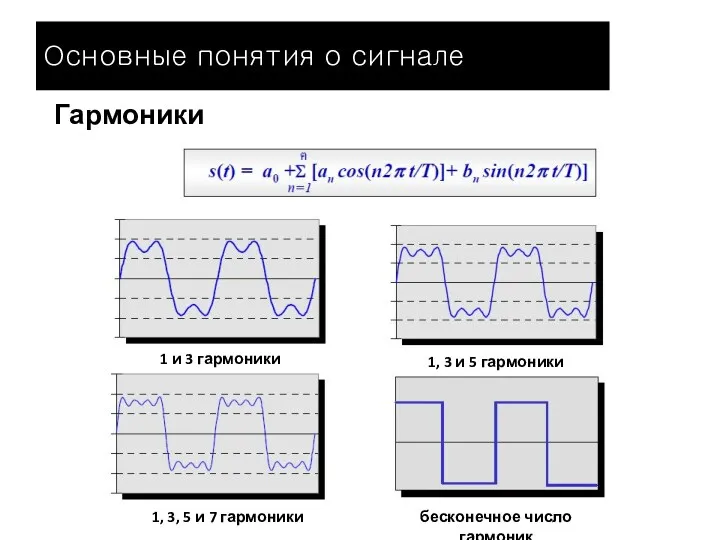
- 15. Гармоники 1 и 3 гармоники 1, 3, 5 и 7 гармоники 1, 3 и 5 гармоники
- 16. Основные понятия о сигнале В зависимости от характера воздействия на сигнал помехи разделяют на аддитивные и
- 17. Основные понятия о сигнале Выделение полезных составляющих из общей суммы зарегистрированных сигналов или максимальное подавление шумов
- 18. Всякое периодическое колебание частоты F можно получить в результате суммирования бесконечного числа гармоник с частотами F,
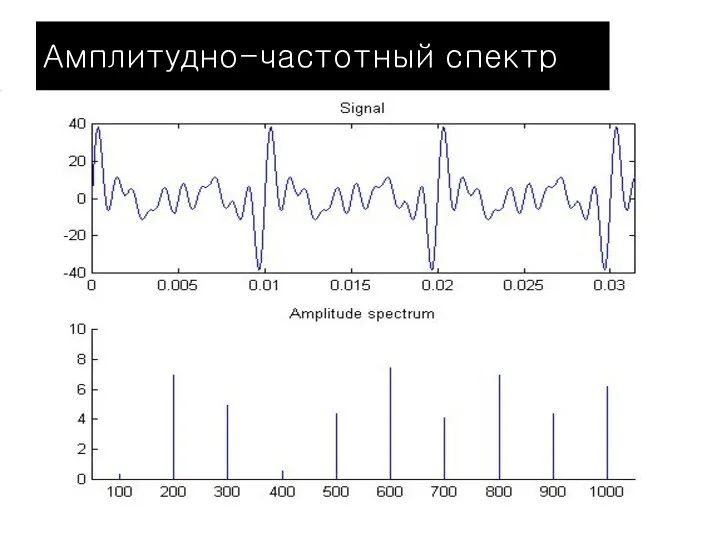
- 19. Амплитудно-частотный спектр
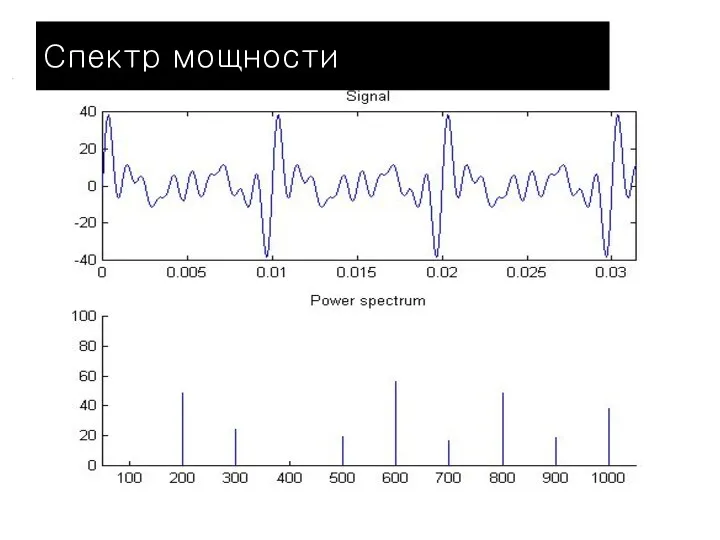
- 20. Спектр мощности
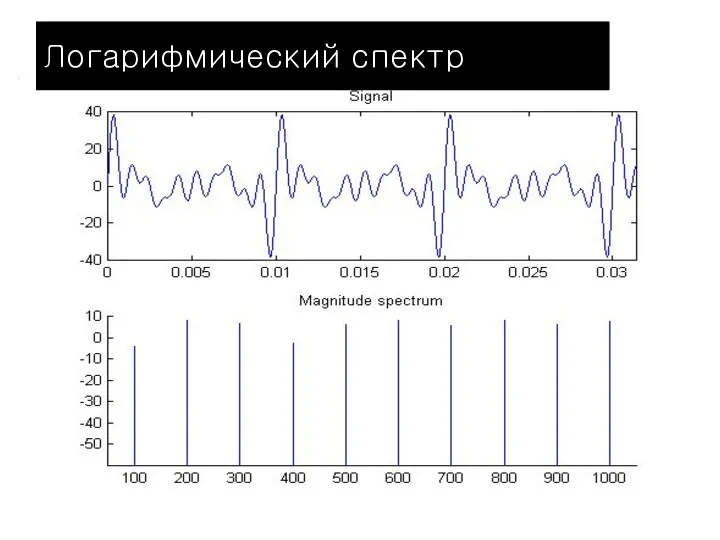
- 21. Логарифмический спектр
- 22. Преобразование Фурье Цифровая обработка сигналов заключается в том, что напряжение, ток, или любой другой физический сигнал
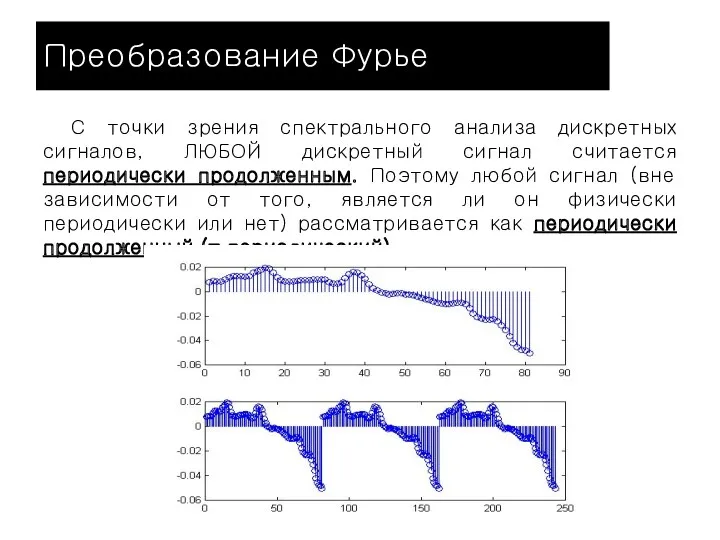
- 23. Преобразование Фурье С точки зрения спектрального анализа дискретных сигналов, ЛЮБОЙ дискретный сигнал считается периодически продолженным. Поэтому
- 24. Раз любой дискретный сигнал рассматривается как периодический (с периодом Т, равным длительности сигнала), то к нему
- 25. Дискретное преобразование Фурье (ДПФ) (Discrete Fourier Transform, DFT) – результат применения теоремы Фурье к дискретному сигналу
- 26. Прямое дискретное преобразование Фурье позволяет получить для цифрового сигнала x(n), период которого задан N точками, N
- 27. Для двух крайних точек в спектре сигнала X(0) и X(N/2) легко определить их значения: и В
- 28. Обратное преобразование Фурье позволяет восстановить сигнал x(n) во временной области по его спектру X(k). Математическая запись
- 29. Свойство 1 Если длина сигнала в отсчетах = N, то количество гармоник в Фурье-разложении также будет
- 30. Пример Пусть частота дискретизации сигнала 16 кГц, длительность сигнала в отсчетах = 160 отсчетов (10 миллисекунд).
- 31. Свойство 2 Если частота дискретизации сигнала = Fs, то частота самой высокой гармоники в ДПФ-разложении равна
- 32. Скорость вычисления спектра Если длина сигнала в отсчетах = N, то общее количество операций, необходимых для
- 33. Быстрое преобразование Фурье (БПФ) (Fast Fourier Transform, FFT) – способ «быстрого» вычисления ДПФ за счет одного
- 34. Если длина сигнала в отсчетах есть степень двойки (например, 256 отсчетов = , 512 отсчетов =
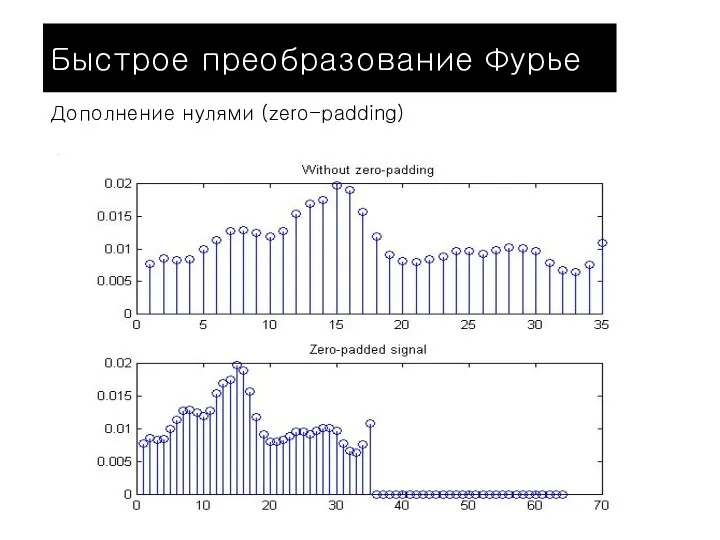
- 35. Быстрое преобразование Фурье Дополнение нулями (zero-padding)
- 36. MATLAB Y = fft(x) - без дополнения нулями (может вычислять ОЧЕНЬ медленно, если длина сигнала x
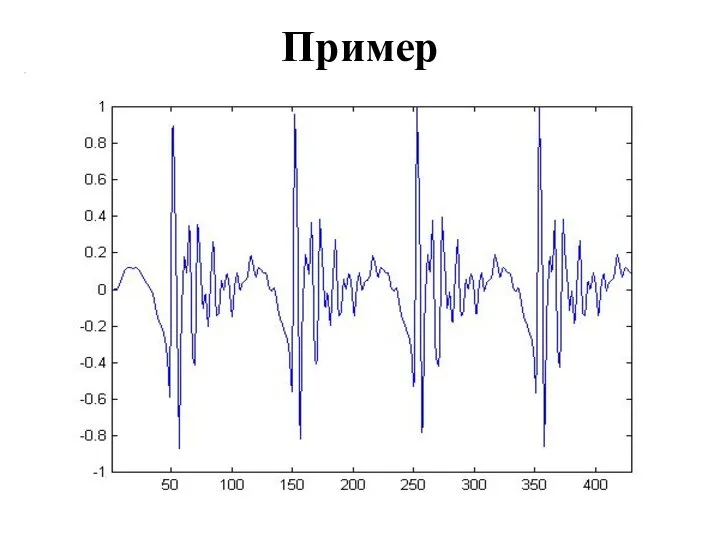
- 37. Пример
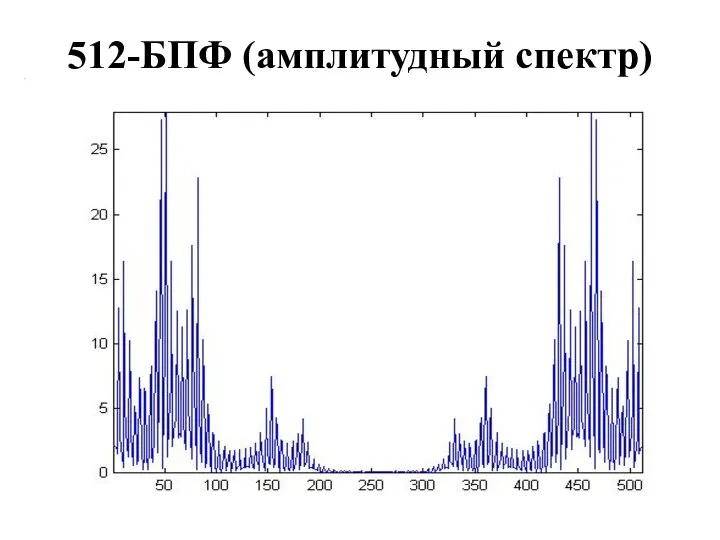
- 38. 512-БПФ (амплитудный спектр)
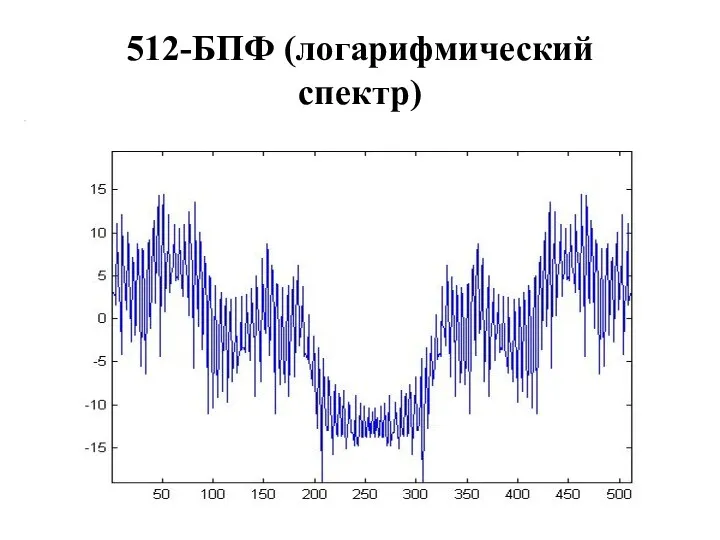
- 39. 512-БПФ (логарифмический спектр)
- 41. Скачать презентацию

















 Автоматизация Р в слогах и словах
Автоматизация Р в слогах и словах Знаменитые жители СПб
Знаменитые жители СПб A Case Bronchitis
A Case Bronchitis Идентификация и фальсификация молочных товаров
Идентификация и фальсификация молочных товаров Испытания в процессе проектирования РЭА
Испытания в процессе проектирования РЭА Шахматные фигуры. Начальная позиция.
Шахматные фигуры. Начальная позиция. Німецька класична філософія 70-ті рр XVIIІ ст. (“коперніканський переворот”)
Німецька класична філософія 70-ті рр XVIIІ ст. (“коперніканський переворот”) Онлайн курс английского языка. Ценностное предложение и УТП
Онлайн курс английского языка. Ценностное предложение и УТП Классный час: Государственные символы РОССИИ. Электронная презентация.
Классный час: Государственные символы РОССИИ. Электронная презентация. Проект: Мир сказок К. И. Чуковского. (средняя группа)
Проект: Мир сказок К. И. Чуковского. (средняя группа) Группа компаний Комитет.Орг. Hr-мероприятия. Деловые события и форумы
Группа компаний Комитет.Орг. Hr-мероприятия. Деловые события и форумы Музыкальная драматургия
Музыкальная драматургия Выселковский район. Вчера, сегодня, завтра.
Выселковский район. Вчера, сегодня, завтра. Иудаизм
Иудаизм Презентация Зимние олимпийские игры в Сочи
Презентация Зимние олимпийские игры в Сочи Знание научное и знание художественное
Знание научное и знание художественное Возбуждение и рассмотрение дела об административном правонарушении
Возбуждение и рассмотрение дела об административном правонарушении Силачи и слабаки в мире кислот и оснований.
Силачи и слабаки в мире кислот и оснований. Интеллектуально-развлекательная игра Морской бой по ПДД
Интеллектуально-развлекательная игра Морской бой по ПДД Συνδρομο υπνικης απνοιας
Συνδρομο υπνικης απνοιας ТЕАТРАЛИЗОВАННАЯ ДЕЯТЕЛЬНОСТЬ – ОДНО ИЗ ПЕРСПЕКТИВНЫХ НАПРАВЛЕНИЙ РАЗВИТИЯ СОВРЕМЕННОГО ДОШКОЛЬНОГО ОБРАЗОВАНИЯ
ТЕАТРАЛИЗОВАННАЯ ДЕЯТЕЛЬНОСТЬ – ОДНО ИЗ ПЕРСПЕКТИВНЫХ НАПРАВЛЕНИЙ РАЗВИТИЯ СОВРЕМЕННОГО ДОШКОЛЬНОГО ОБРАЗОВАНИЯ Peek-a-Boo
Peek-a-Boo День России
День России Цифро-аналоговый преобразователь: структурная схема и принцип действия
Цифро-аналоговый преобразователь: структурная схема и принцип действия Социальный состав населения России на 1897 год
Социальный состав населения России на 1897 год Германия (11 класс)
Германия (11 класс) Сестринский процесс при эпидемическом паротите, ветряной оспе
Сестринский процесс при эпидемическом паротите, ветряной оспе Экономическая политика Петра I
Экономическая политика Петра I