Содержание
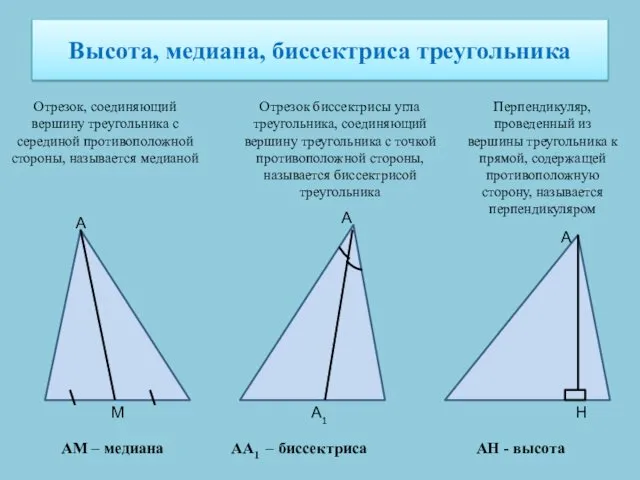
- 2. Высота, медиана, биссектриса треугольника Отрезок, соединяющий вершину треугольника с серединой противоположной стороны, называется медианой А М
- 3. Средняя линия треугольника Средней линией треугольника называется отрезок, соединяющий середины двух его сторон. К М КМ
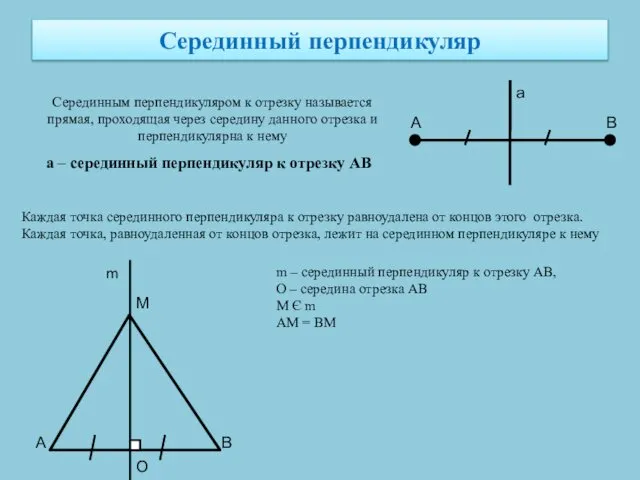
- 4. Cерединный перпендикуляр Серединным перпендикуляром к отрезку называется прямая, проходящая через середину данного отрезка и перпендикулярна к
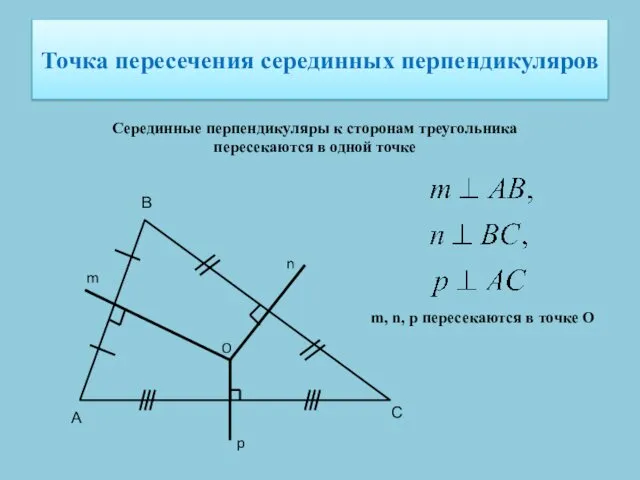
- 5. Точка пересечения серединных перпендикуляров Серединные перпендикуляры к сторонам треугольника пересекаются в одной точке А В С
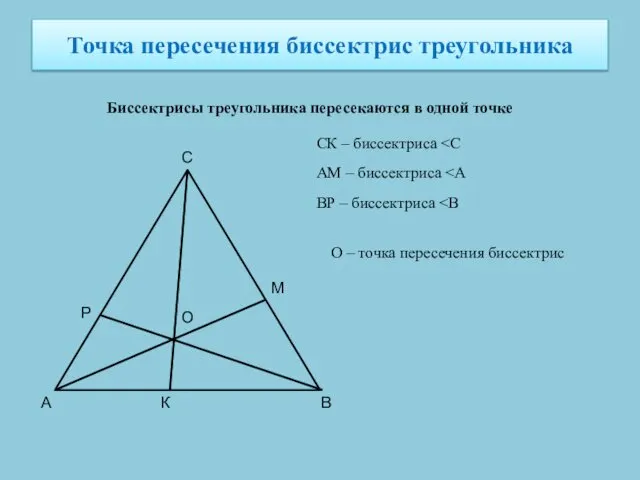
- 6. Точка пересечения биссектрис треугольника Биссектрисы треугольника пересекаются в одной точке А В С К СК –
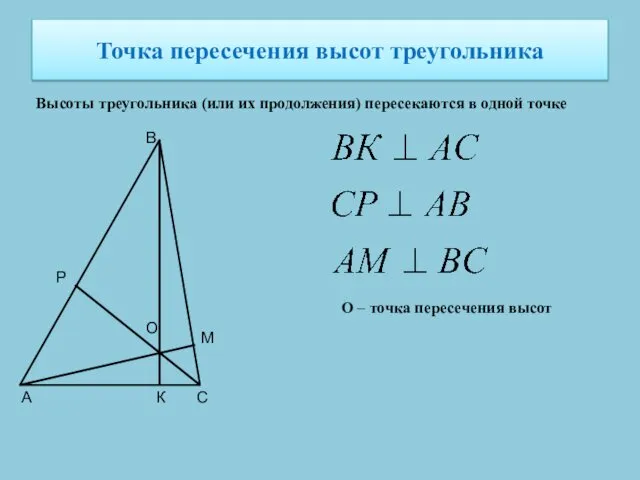
- 7. Точка пересечения высот треугольника Высоты треугольника (или их продолжения) пересекаются в одной точке А С В
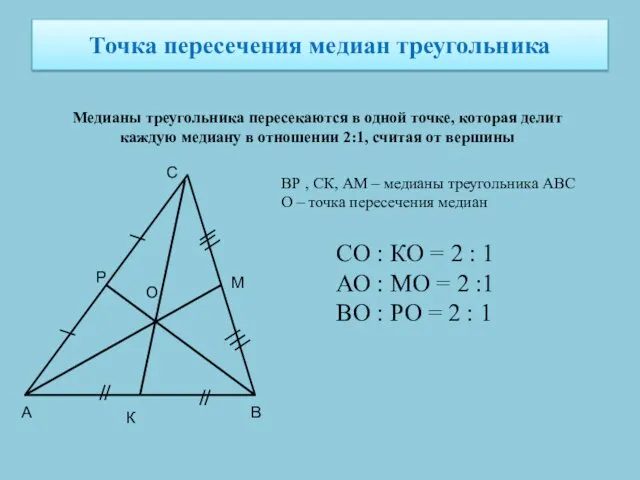
- 8. Точка пересечения медиан треугольника Медианы треугольника пересекаются в одной точке, которая делит каждую медиану в отношении
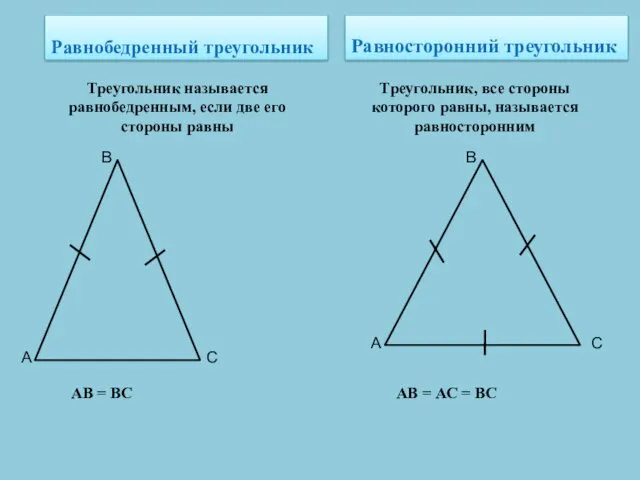
- 9. Равнобедренный треугольник Равносторонний треугольник Треугольник называется равнобедренным, если две его стороны равны Треугольник, все стороны которого
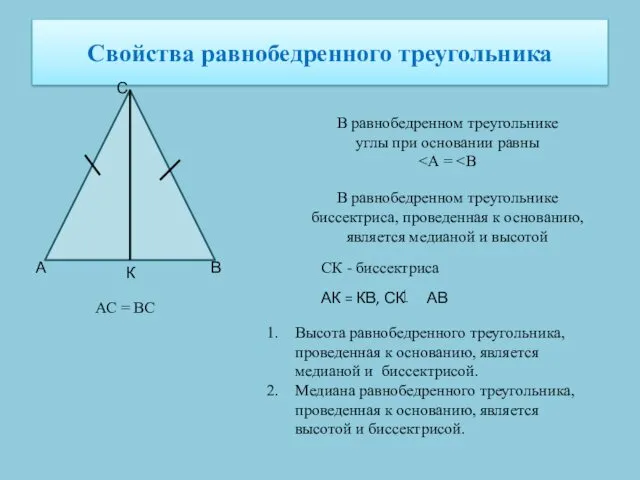
- 10. Свойства равнобедренного треугольника А С В В равнобедренном треугольнике углы при основании равны В равнобедренном треугольнике
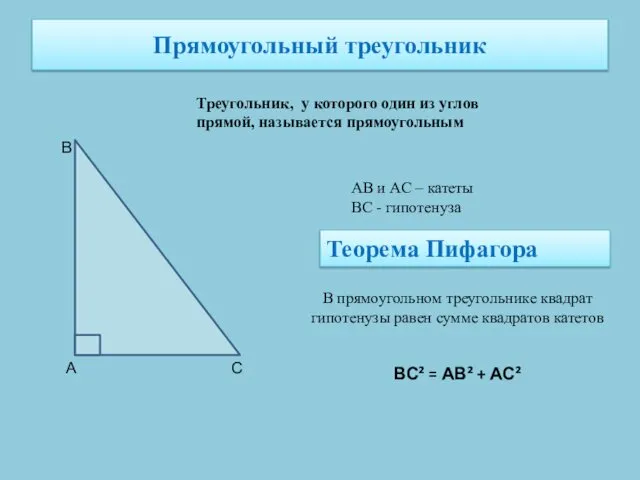
- 11. Прямоугольный треугольник Треугольник, у которого один из углов прямой, называется прямоугольным АВ и АС – катеты
- 12. Свойства прямоугольного треугольника Сумма двух острых углов прямоугольного треугольника равна 90° Катет прямоугольного треугольника, лежащий против
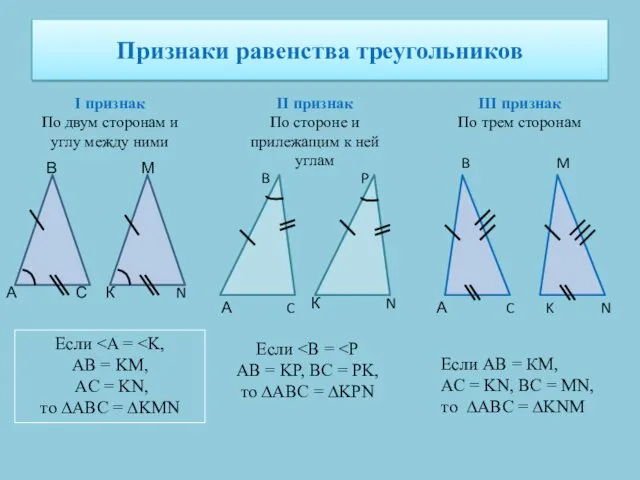
- 13. Признаки равенства треугольников I признак По двум сторонам и углу между ними II признак По стороне
- 14. Признаки равенства прямоугольных треугольников По двум катетам Если АВ = КМ, АС = KN, то ∆АВС
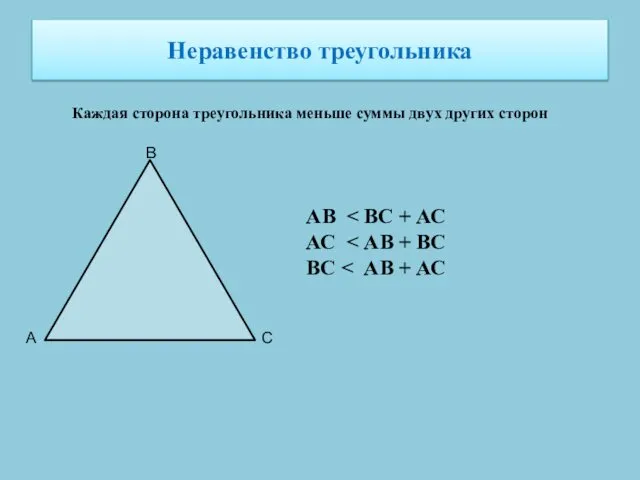
- 15. Неравенство треугольника Каждая сторона треугольника меньше суммы двух других сторон А В С АВ АС ВС
- 16. Сумма углов треугольника равна 180° A B C Угол, смежный с каким-нибудь углом треугольника, называется внешним
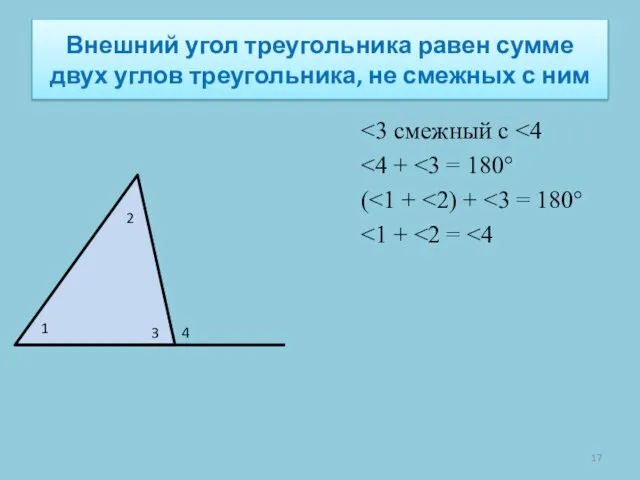
- 17. Внешний угол треугольника равен сумме двух углов треугольника, не смежных с ним ( 1 2 3
- 18. Зависимость между величинами сторон и углов треугольника В треугольнике: 1) против большей стороны лежит больший угол;
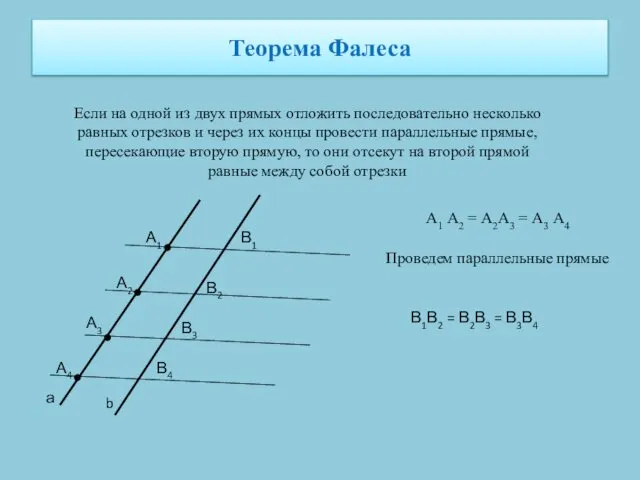
- 19. Теорема Фалеса Если на одной из двух прямых отложить последовательно несколько равных отрезков и через их
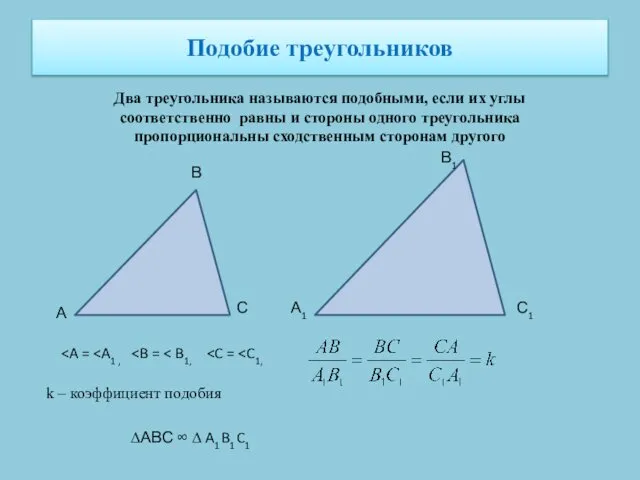
- 20. Подобие треугольников Два треугольника называются подобными, если их углы соответственно равны и стороны одного треугольника пропорциональны
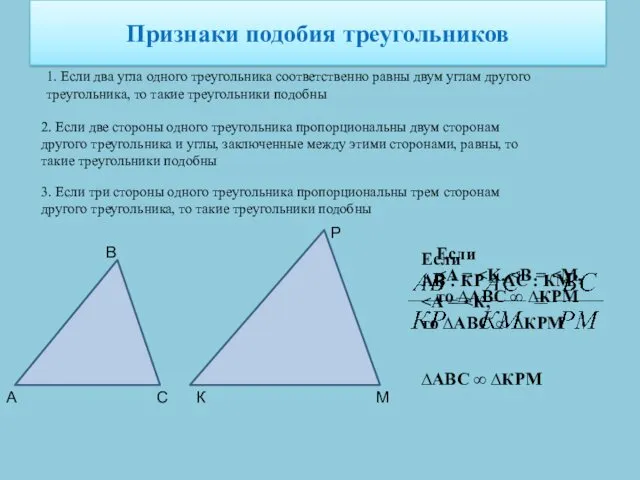
- 21. Признаки подобия треугольников 1. Если два угла одного треугольника соответственно равны двум углам другого треугольника, то
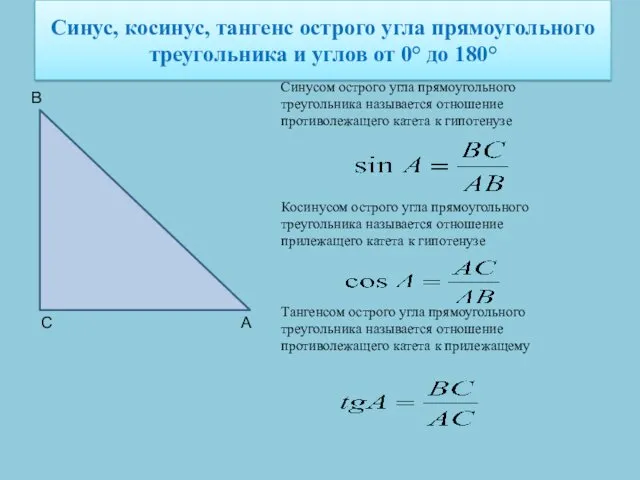
- 22. Синус, косинус, тангенс острого угла прямоугольного треугольника и углов от 0° до 180° С А В
- 23. Основное тригонометрическое тождество sin² x + cos² x = 1 Теорема о площади треугольника Площадь треугольника
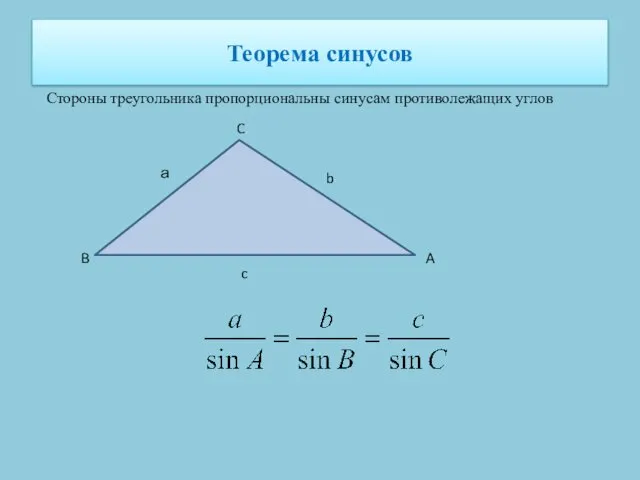
- 24. Теорема синусов Стороны треугольника пропорциональны синусам противолежащих углов а b c C B A
- 25. Теорема косинусов Квадрат стороны треугольника равен сумме квадратов двух других сторон минус удвоенное произведение этих сторон
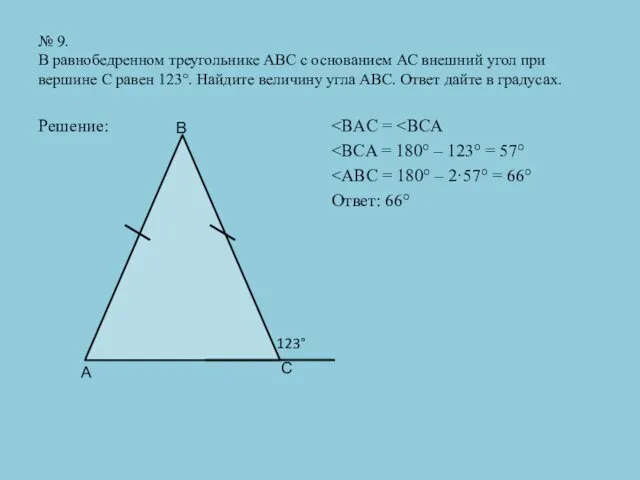
- 26. № 9. В равнобедренном треугольнике АВС с основанием АС внешний угол при вершине С равен 123°.
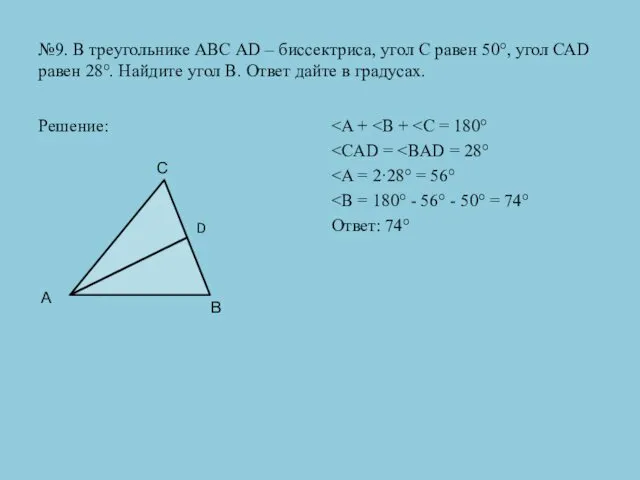
- 27. №9. В треугольнике АВС АD – биссектриса, угол С равен 50°, угол САD равен 28°. Найдите
- 28. №9. Один острый угол прямоугольного треугольника в два раза больше другого. Найдите меньший острый угол. Ответ
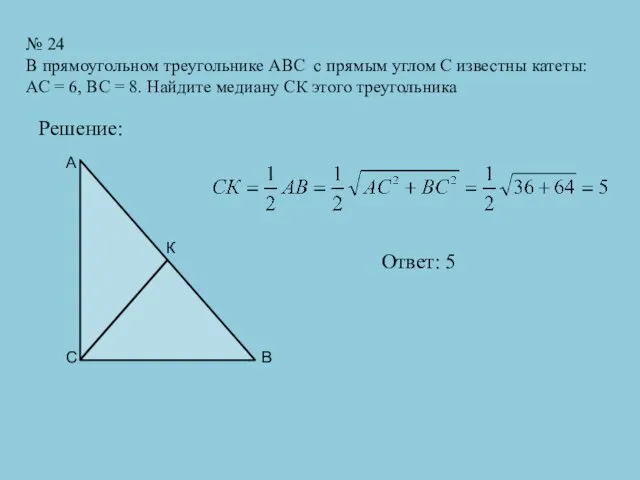
- 29. № 24 В прямоугольном треугольнике АВС с прямым углом С известны катеты: АС = 6, ВС
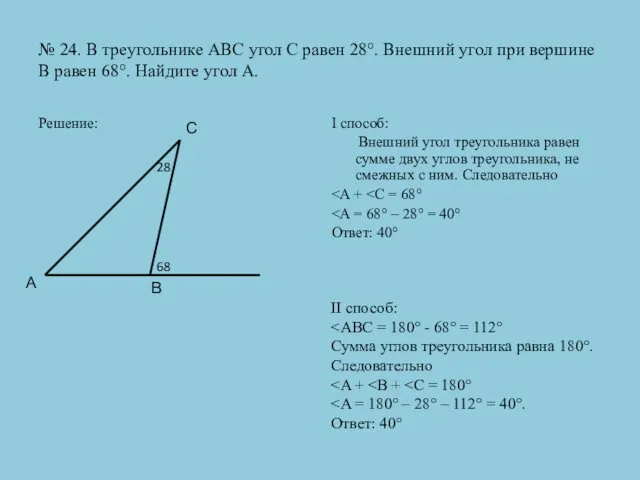
- 30. № 24. В треугольнике АВС угол С равен 28°. Внешний угол при вершине В равен 68°.
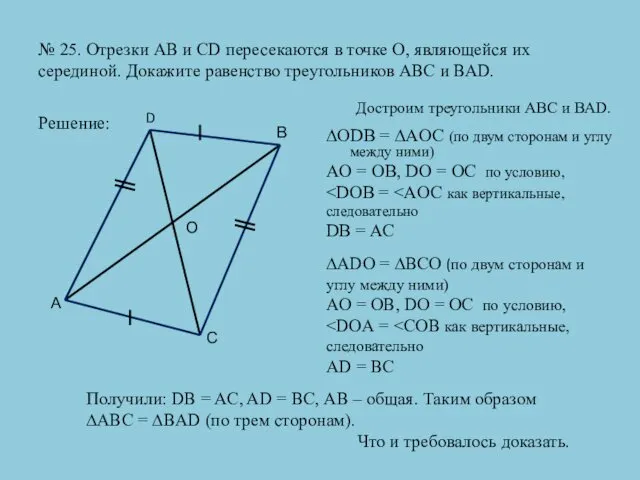
- 31. № 25. Отрезки АВ и CD пересекаются в точке О, являющейся их серединой. Докажите равенство треугольников
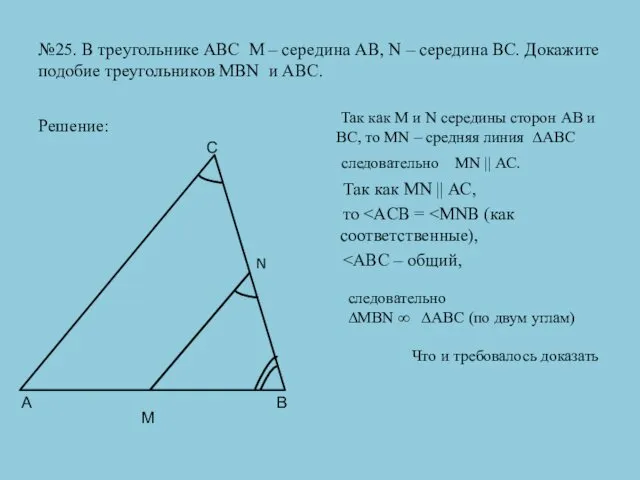
- 32. №25. В треугольнике АВС М – середина АВ, N – середина ВС. Докажите подобие треугольников MBN
- 34. Скачать презентацию








 Педагогический Проект Коррекция речевых нарушений у детей старшего дошкольного возраста посредством развития мелкой моторики
Педагогический Проект Коррекция речевых нарушений у детей старшего дошкольного возраста посредством развития мелкой моторики Игровые технологии как средства формирования коммуникативной компетенции учащихся.
Игровые технологии как средства формирования коммуникативной компетенции учащихся. История домонгольской Руси
История домонгольской Руси Презентация первого урока Город, комфортный для жизни
Презентация первого урока Город, комфортный для жизни Что такое семейные реликвии
Что такое семейные реликвии Развитие медицины сегодня, её роль в обществе. Современное состояние медицины в РК
Развитие медицины сегодня, её роль в обществе. Современное состояние медицины в РК Снижение потерь электроэнергии путем компенсации реактивной мощности
Снижение потерь электроэнергии путем компенсации реактивной мощности Линейные вычислительные алгоритмы
Линейные вычислительные алгоритмы Оределяем темперамент ребенкап
Оределяем темперамент ребенкап Подвижные установки для дегазации и азотирования масла
Подвижные установки для дегазации и азотирования масла Програми-архіватори. Операції над архівами (урок 8, 8клас)
Програми-архіватори. Операції над архівами (урок 8, 8клас)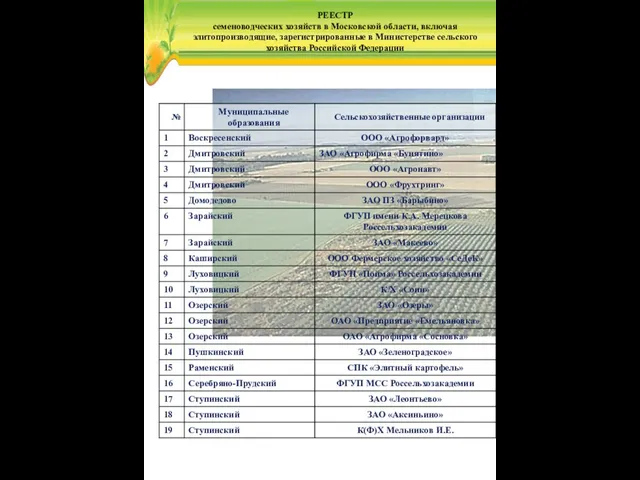 Реестр семеноводческих хозяйств в Московской области, включая элитопроизводящие, зарегистрированные в Министерстве сельского хозяйства
Реестр семеноводческих хозяйств в Московской области, включая элитопроизводящие, зарегистрированные в Министерстве сельского хозяйства Автомобилестроительная корпорация Toyota Motor Corporation
Автомобилестроительная корпорация Toyota Motor Corporation Альтернатива использования мёда в производстве молочных продуктов
Альтернатива использования мёда в производстве молочных продуктов Общество с ограниченной ответственностью Астериас. Промышленная фильтрация. Инжиниринг
Общество с ограниченной ответственностью Астериас. Промышленная фильтрация. Инжиниринг История создания швейной машинки
История создания швейной машинки Оформление реферата по зоопсихологии
Оформление реферата по зоопсихологии Шефская работа. Викторина для мальчиков и девочек.
Шефская работа. Викторина для мальчиков и девочек. Интеллектуальная игра Самый умный
Интеллектуальная игра Самый умный Interaktivnaya_igra_Den_rossiyskoy_nauki
Interaktivnaya_igra_Den_rossiyskoy_nauki ЛОГОПЕДИЧЕСКИЙ АЛЬБОМ
ЛОГОПЕДИЧЕСКИЙ АЛЬБОМ Виды речевой и читательской деятельности
Виды речевой и читательской деятельности Память героям Отечества
Память героям Отечества Туляремия
Туляремия Деятельностный подход в обучении географии
Деятельностный подход в обучении географии Презентация Природные источники углеводородов
Презентация Природные источники углеводородов Работа с молодыми специалистами
Работа с молодыми специалистами Бесік жыры
Бесік жыры