Содержание
- 2. Задача № 1 С помощью критерия Михайлова оценить устойчивость АС, характеристическое уравнение которой имеет вид: 0,0014р4+0,022р3+0,7р2+1,6р+5=0
- 3. Задаваясь различными значениями частоты ω построим годограф вектор-функции Михайлова: Х(ω)=5-0,7ω2+0,0014ω4 Y(ω)=1,6ω-0,022ω3 Исходная АС 4-го порядка и
- 4. Задача №2 Определить устойчивость АС с характеристическим уравнением р5+р4+3р3+2р2+р+0,5=0 Решение: Функция Михайлова А(jω)=(jω)5+(jω)4+3(jω)3+2(jω)2+(jω)+0,5= jω5+ω4-j3ω3-2ω2 +jω+0,5= =ω4-2ω2+0,5+j(ω5-3ω3+ω)
- 5. ω5-3ω3+ω=0 ω3=0 ω4-3ω2+1=0 2,6 0,4 ω4=1,6; ω6=0,63 Располагаем корни в порядке возрастания ω3=0, ω2=0,55, ω5=0,63, ω1=1,3;
- 6. Методика оценки устойчивости системы по следствию критерия Михайлова: а) определяем для замкнутой АС функцию Михайлова А(jω)=X(ω)+jY(ω).
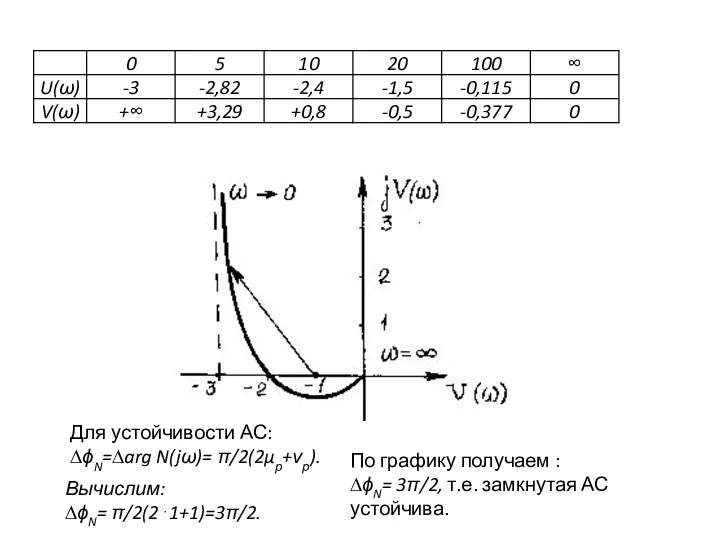
- 7. Задача №3 Определить устойчивость замкнутой АС по критерию Найквиста, если её передаточная функция в разомкнутом состоянии
- 8. Для устойчивости АС: ∆ϕN=∆arg N(jω)= π/2(2μр+νр). По графику получаем : ∆ϕN= 3π/2, т.е. замкнутая АС устойчива.
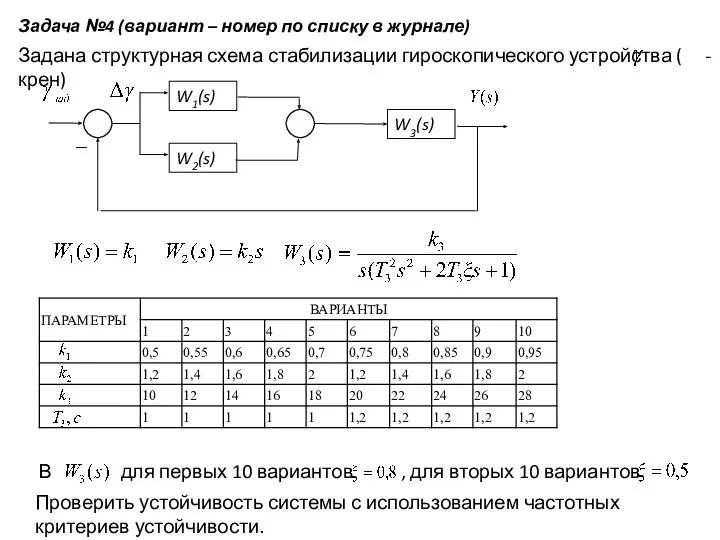
- 9. Задана структурная схема стабилизации гироскопического устройства ( -крен) В для первых 10 вариантов , для вторых
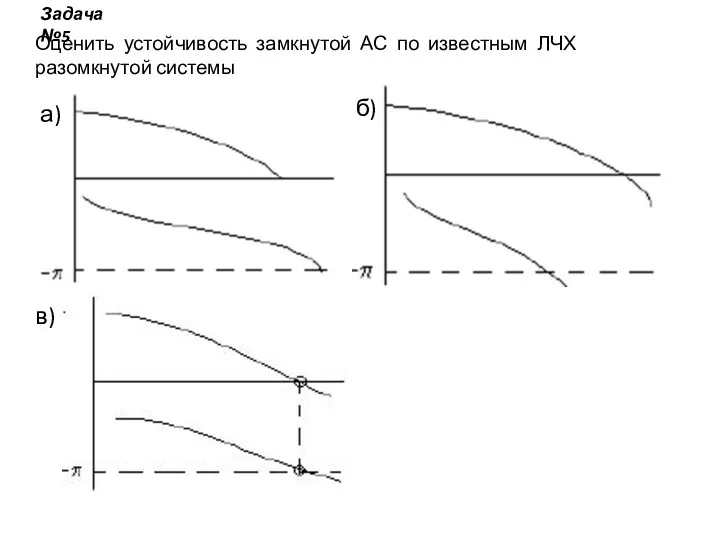
- 10. а) б) в) Оценить устойчивость замкнутой АС по известным ЛЧХ разомкнутой системы Задача №5
- 12. Скачать презентацию






 Тема 2.3 Устранение мелких неисправностей
Тема 2.3 Устранение мелких неисправностей Вышивка гладью
Вышивка гладью Игры на развитие речи детей 2-3 лет
Игры на развитие речи детей 2-3 лет Особенности неврологического осмотра в сосудистой нейрореанимации
Особенности неврологического осмотра в сосудистой нейрореанимации Путешествие в мир доброты
Путешествие в мир доброты Духовная культура. Роль религии в жизни общества
Духовная культура. Роль религии в жизни общества Передовые производственные технологии и роботехника
Передовые производственные технологии и роботехника Цветные сплавы
Цветные сплавы Организация процессов по разработке сайта
Организация процессов по разработке сайта Презентация по теме: Развитие внимания
Презентация по теме: Развитие внимания Состав дорожного полотна
Состав дорожного полотна ВЗАИМОДЕЙСТВИЕ ШКОЛЫ И СЕМЬИ В ДУХОВНО-НРАВСТВЕННОМ ВОСПИТАНИИ МЛАДШЕГО ШКОЛЬНИКА
ВЗАИМОДЕЙСТВИЕ ШКОЛЫ И СЕМЬИ В ДУХОВНО-НРАВСТВЕННОМ ВОСПИТАНИИ МЛАДШЕГО ШКОЛЬНИКА Учебно-методический комплекс Планета знаний
Учебно-методический комплекс Планета знаний Мохнатая азбука. Б. Заходер К уроку внеклассного чтения в 1 классе
Мохнатая азбука. Б. Заходер К уроку внеклассного чтения в 1 классе Асылдандыру жұмыстары
Асылдандыру жұмыстары Плавкие предохранители выше 1 кВ
Плавкие предохранители выше 1 кВ Методическая разработка урока ВОДОРОД 8 класс
Методическая разработка урока ВОДОРОД 8 класс Қызыл жазық теміреткі
Қызыл жазық теміреткі Михаил Евграфович Салтыков-Щедрин
Михаил Евграфович Салтыков-Щедрин Презентация по окружающему миру 5 классДНК.РНК. АТФ
Презентация по окружающему миру 5 классДНК.РНК. АТФ Три состояния воды
Три состояния воды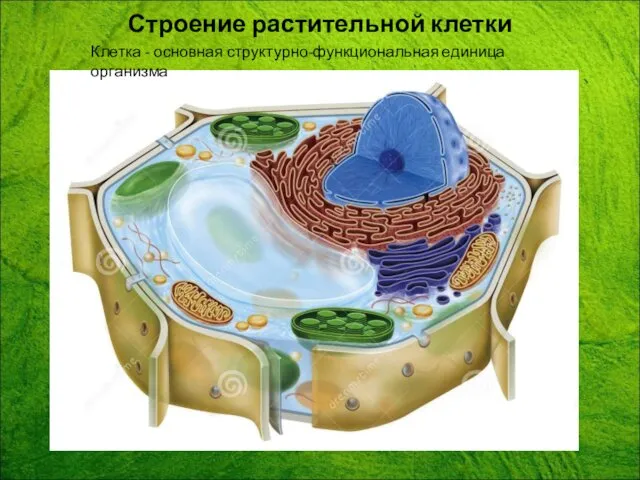 Строение растительной клетки
Строение растительной клетки Обогащение полезных ископаемых. Измельчение и классификация
Обогащение полезных ископаемых. Измельчение и классификация Информация, свойства, системы счисления, измерение и представление текстовой и графической информации
Информация, свойства, системы счисления, измерение и представление текстовой и графической информации Ефективна інституція урядового контролю в Україні
Ефективна інституція урядового контролю в Україні Особенности преобразователей большой и средней мощности
Особенности преобразователей большой и средней мощности Адаптация ребенка к условиям дошкольного образовательного учреждения
Адаптация ребенка к условиям дошкольного образовательного учреждения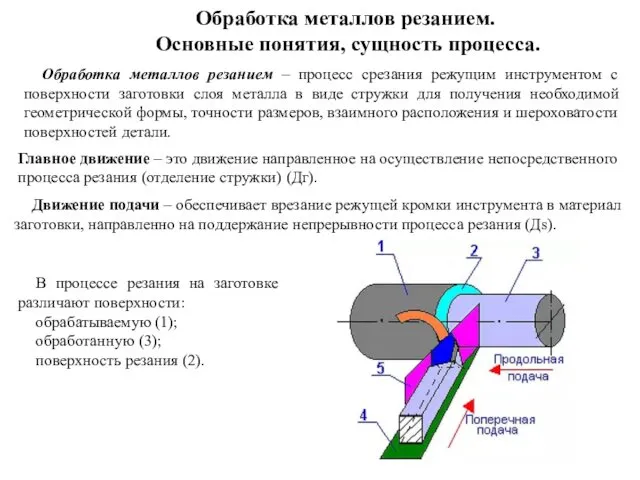 Обработка металлов резанием
Обработка металлов резанием