Содержание
- 2. 1.1. Понятие вектора Мы знаем, что есть 2 вида величин. Например, длина, площадь, объем, масса и
- 3. F
- 4. Аналогично можно ввести понятие геометрического вектора. В отличие от физических векторов, векторы в геометрии не имеют
- 5. 1.2. Равенство векторов Длину отрезка АВ называют модулем вектора AB и обозначают так: |AB|. Аналогично, модуль
- 6. Если векторы а и b лежат на перпендикулярных прямых, то их называют перпендикулярными (ортогональными) векторами и
- 7. 1.3.Cвойства равных векторов Теорема. Равные векторы можно совместить параллельным переносом, и, обратно, если векторы совмещаются парллельным
- 8. А В С D
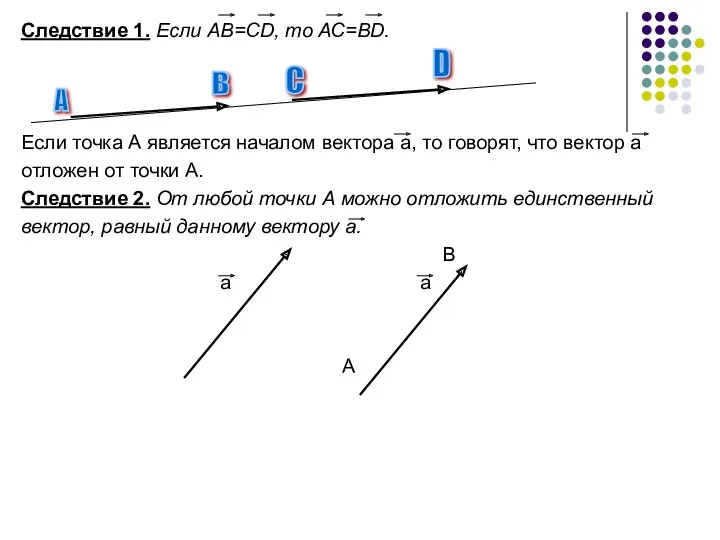
- 9. Следствие 1. Если АВ=СD, то АС=ВD. Если точка А является началом вектора а, то говорят, что
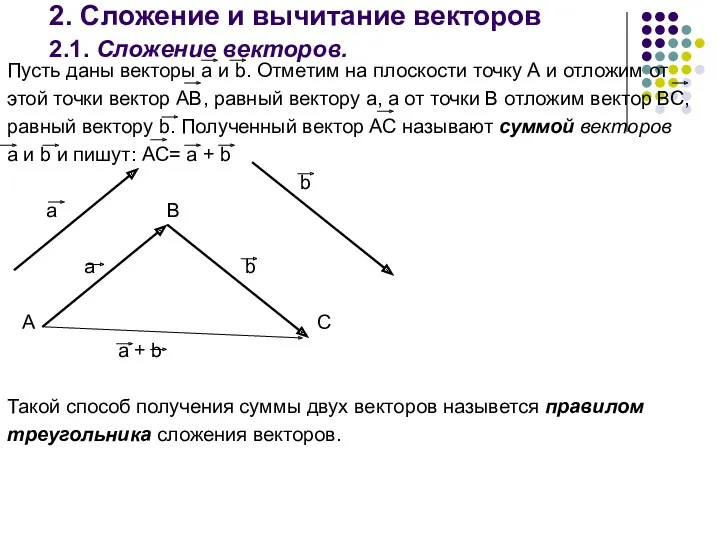
- 10. 2. Сложение и вычитание векторов 2.1. Сложение векторов. Пусть даны векторы а и b. Отметим на
- 11. 2.2. Свойства сложения векторов Теорема 1. Для любых векторов a, b и c верно: 1. а+b=b+a
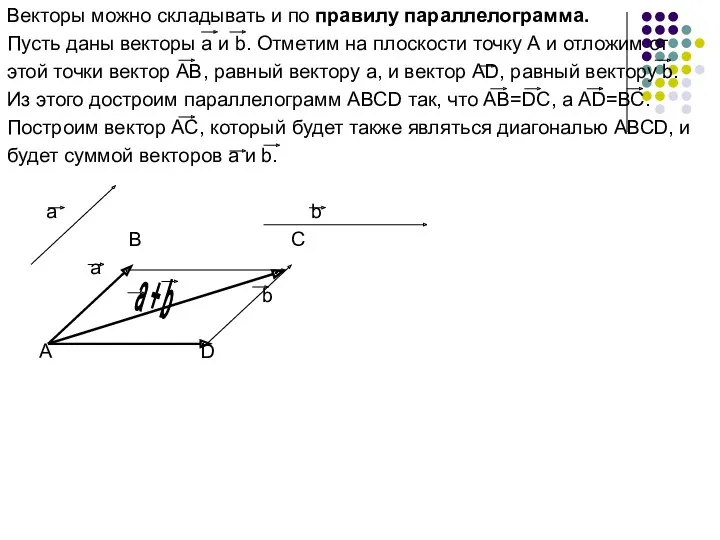
- 12. Векторы можно складывать и по правилу параллелограмма. Пусть даны векторы а и b. Отметим на плоскости
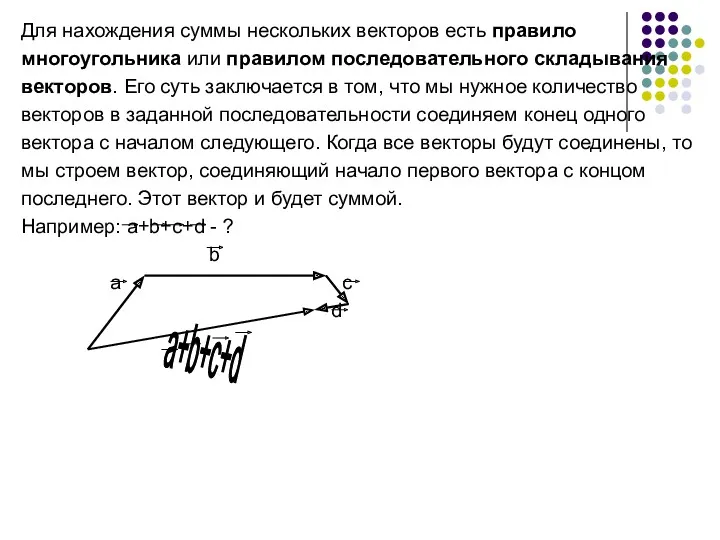
- 13. Для нахождения суммы нескольких векторов есть правило многоугольника или правилом последовательного складывания векторов. Его суть заключается
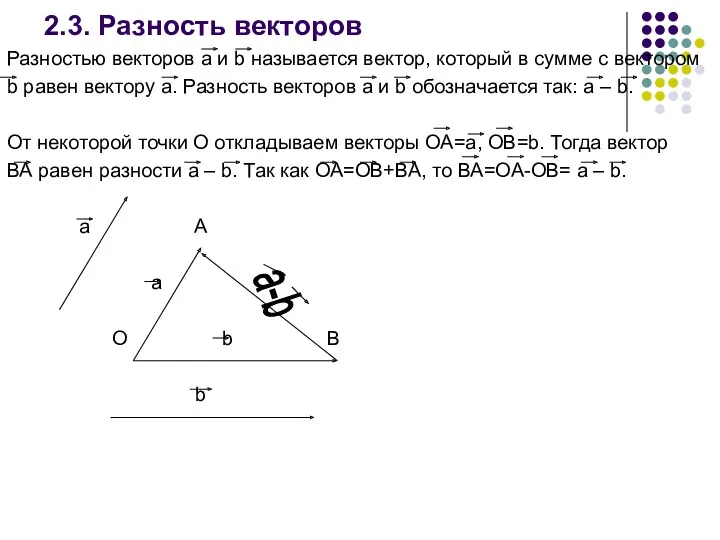
- 14. 2.3. Разность векторов Разностью векторов а и b называется вектор, который в сумме с вектором b
- 15. 3.1. Умножение вектора на число и его свойства Произведением вектора а≠0 на число К называется вектор,
- 16. 3.2. Признак коллинеарности векторов Теорема. Чтобы вектор b был коллинеарен ненулевому вектору а, необходимо и достаточно
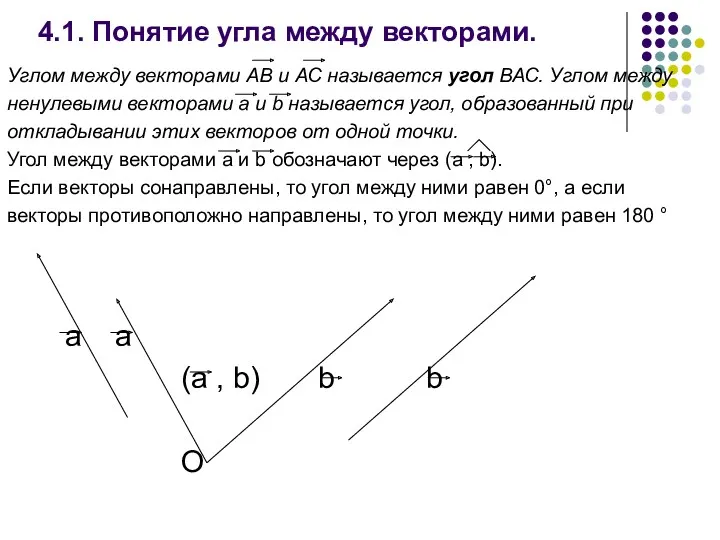
- 17. 4.1. Понятие угла между векторами. Углом между векторами АВ и АС называется угол ВАС. Углом между
- 18. 4.2. Скалярное произведение векторов Скалярным произведением двух векторов называется число, равное произведению модулей этих векторов на
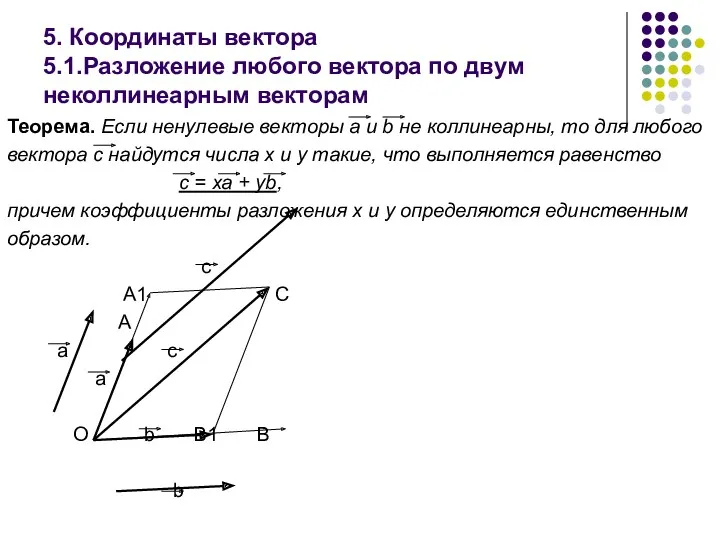
- 19. 5. Координаты вектора 5.1.Разложение любого вектора по двум неколлинеарным векторам Теорема. Если ненулевые векторы а и
- 20. Из этой теоремы вытекает, что любой вектор можно разложить по двум произвольным неколлинеарным векторам. Если на
- 21. 5.2. Координаты вектора в прямоугольной системе координат. Рассмотрим прямоугольную систему координат Оху. Пусть i- единичный вектор,
- 22. Некоторые свойства координат вектора: 1. У равных векторов соответствующие координаты равны: если а= (х; у), b=
- 23. 5.3. Координаты вектора, заданного координатами концов. Радиус-вектор Если на плоскости Оху задана точка А (х;у), то
- 24. 6.Выражение скалярного произведения через координаты векторов 6.1.Координатный вид скалярного произведения Скалярное произведение векторов а = (х1;у1)
- 25. 6.2. Координатный вид коллинеарности и перпенди- кулярности векторов. Определение угла между векторами Если векторы а=(х1;у1) и
- 26. 7.1. Уравнение прямой. Направляющий вектор и вектор нормали прямой Уравнение прямой можно задать различными способами. Например,
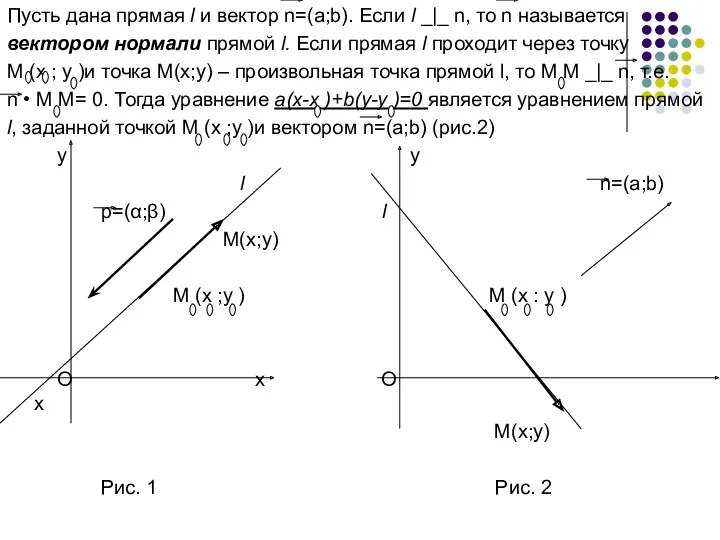
- 27. Пусть дана прямая l и вектор n=(a;b). Если l _|_ n, то n называется вектором нормали
- 29. Скачать презентацию
















 Инструкция по монтажу обтекателя НЕКСТ без сверления
Инструкция по монтажу обтекателя НЕКСТ без сверления Организация и проведение общего собрания собственников помещений в многоквартирном доме в целях проведения капитального ремонта
Организация и проведение общего собрания собственников помещений в многоквартирном доме в целях проведения капитального ремонта Урок-презентация
Урок-презентация Водный туризм, занятие 1
Водный туризм, занятие 1 Конструктивное решение конфликтов в молодежной среде
Конструктивное решение конфликтов в молодежной среде Аммиак
Аммиак Проект Русь моя, жизнь моя. Посвящён Александру Александровичу Блоку
Проект Русь моя, жизнь моя. Посвящён Александру Александровичу Блоку Общая собственность на приватизированное жилище
Общая собственность на приватизированное жилище Отчет о результатах деятельности за 11 месяцев МУП ВГЭС
Отчет о результатах деятельности за 11 месяцев МУП ВГЭС Псков – город воинской славы
Псков – город воинской славы Что мы Родиной зовём ? Подготовительная к школе группа.
Что мы Родиной зовём ? Подготовительная к школе группа. Искусство Киевской Руси X –XIII вв. Галич
Искусство Киевской Руси X –XIII вв. Галич Презентация Детско-родительские отношения.
Презентация Детско-родительские отношения. Итальянский театр Малибран
Итальянский театр Малибран Акция Добрые дела осенью
Акция Добрые дела осенью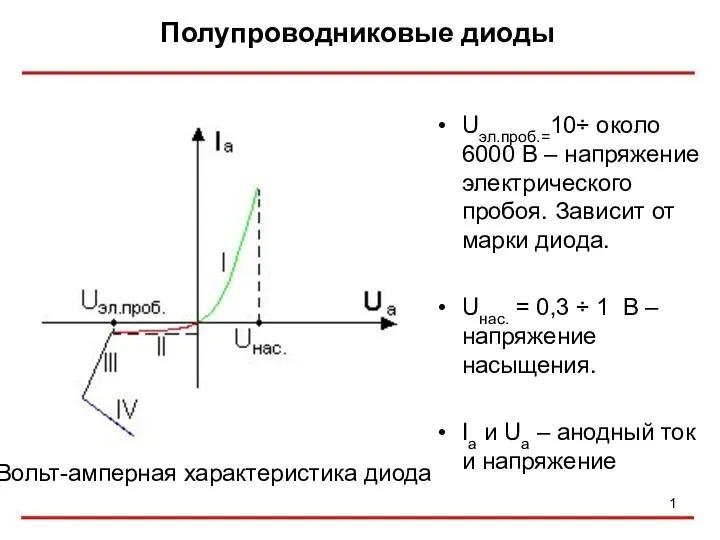 Полупроводниковые диоды
Полупроводниковые диоды Фламенко
Фламенко Топливная промышленность России
Топливная промышленность России Отчет о ходе внедрения проекта 5С, ТРМ и Процессного подхода (шаблон)
Отчет о ходе внедрения проекта 5С, ТРМ и Процессного подхода (шаблон) Сельское хозяйство
Сельское хозяйство Основы теории радиолокационных систем и комплексов
Основы теории радиолокационных систем и комплексов Технологические основы ведения отрасли кролиководства и пушного звероводства
Технологические основы ведения отрасли кролиководства и пушного звероводства Логика высказываний. (Лекция 2)
Логика высказываний. (Лекция 2) Постсекреторная динамика сигнальных соединений. Специфические транспортные белки
Постсекреторная динамика сигнальных соединений. Специфические транспортные белки Презентация на тему Эмоции
Презентация на тему Эмоции Портфолио Чубыкиной Ирины Юрьевны воспитателя МБДОУ Детский сад №18 Колобок г. Брянск (часть IV)
Портфолио Чубыкиной Ирины Юрьевны воспитателя МБДОУ Детский сад №18 Колобок г. Брянск (часть IV) Countries & Nationalities
Countries & Nationalities Гидротехнические сооружения. Виды бетонных плотин
Гидротехнические сооружения. Виды бетонных плотин