Содержание
- 2. Радианная мера угла Центральный угол, опирающийся на дугу, длина которой равна радиусу окружности, называется углом в
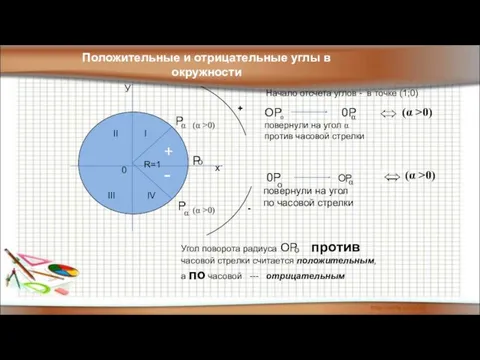
- 3. + - Р (α >0) α (α >0) Р α У х 0 Положительные и отрицательные
- 4. * Радианная мера угла Единичной окружностью называется окружность с центром в начале координат и радиусом, равным
- 5. Числовая окружность. Начало отсчета числовой прямой, единичный отрезок которой равен радиусу единичной окружности, совместим с концом
- 6. Начало отсчета числовой прямой, единичный отрезок которой равен радиусу единичной окружности, совместим с концом одного из
- 7. И так далее… Числовая окружность. Проследите за тем как откладываются на числовой окружности положительные числа. Очевидно,
- 8. И так далее… Числовая окружность. Проследите за тем как откладываются на числовой окружности отрицательные числа.
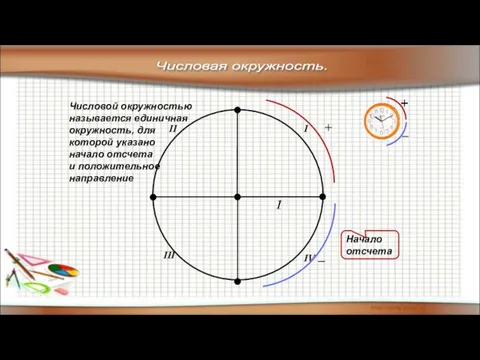
- 9. Числовая окружность. Числовой окружностью называется единичная окружность, для которой указано начало отсчета и положительное направление I
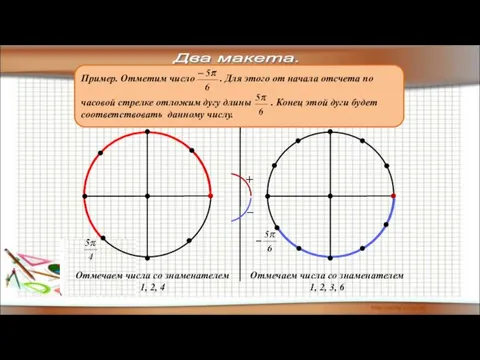
- 10. Два макета. Окружность поделена на восемь равных дуг (каждая дуга =π/4) Окружность поделена на двенадцать равных
- 11. Некоторые свойства. Точке числовой окружности, в отличии от точки числовой прямой, соответствует не одно число. ?
- 12. Некоторые свойства. Симметрия относительно центра окружности ? ? Числам t и t +πk (k ϵ Z)
- 13. Некоторые свойства. Числам t и –t соответствуют точки, симметричные относительно горизонтального диаметра. Симметрия относительно горизонтального диаметра
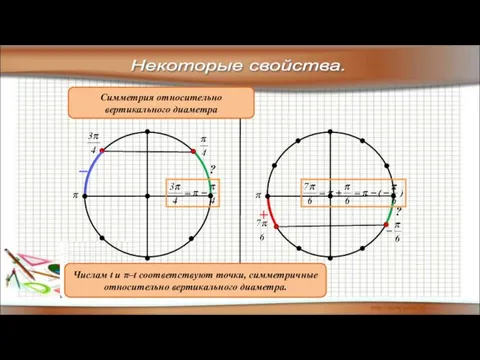
- 14. Некоторые свойства. Числам t и π–t соответствуют точки, симметричные относительно вертикального диаметра. Симметрия относительно вертикального диаметра
- 15. Как отметить на окружности большие числа? Подумай, как воспользоваться свойством и составь алгоритм Потренируйся выполнять первый
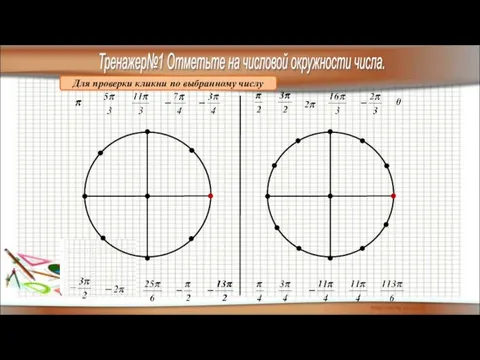
- 16. Тренажер№1 Отметьте на числовой окружности числа. Для проверки кликни по выбранному числу
- 17. Тренажер№2 Подпишите точки окружности. tϵ[0;2π]. очистить Для проверки кликни по выбранной точке
- 18. Тренажер№3 Подпишите точки окружности. tϵ[-2π;0]. очистить Для проверки кликни по выбранной точке
- 19. Тренажер№4 Подпишите точки окружности. tϵ[2π;4π]. очистить Для проверки кликни по выбранной точке
- 20. Определение синуса, косинуса и тангенса угла Косинусом угла называется абсцисса точки, полученной поворотом точки (1;0) вокруг
- 21. Определение синуса, косинуса и тангенса угла Тангенсом угла называется отношение синуса угла к его косинусу (обозначается
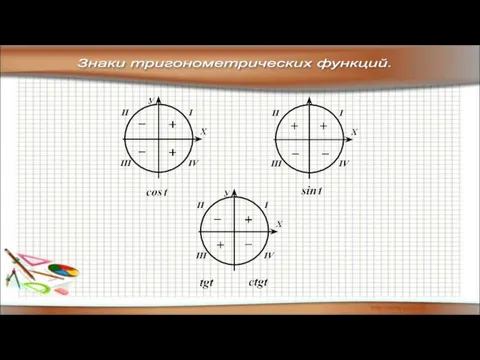
- 22. Знаки тригонометрических функций. I II III IV I II III IV I II III IV
- 23. Зависимость между синусом, косинусом и тангенсом одного и того же угла - основное тригонометрическое тождество. Из
- 24. Зависимость между синусом, косинусом и тангенсом одного и того же угла Выясним теперь зависимость между тангенсом
- 25. *
- 26. Пусть точки М1 и М2 единичной окружности получены поворотом точки Р(1;0) на углы и соответственно). Тогда
- 27. Формулы сложения Теорема. Для любых и справедливо равенство
- 28. Синус, косинус и тангенс двойного угла Выведем формулы синуса и косинуса двойного угла, используя формулы сложения.
- 29. Тригонометрические функции числового аргумента. y = sin x y = cos x
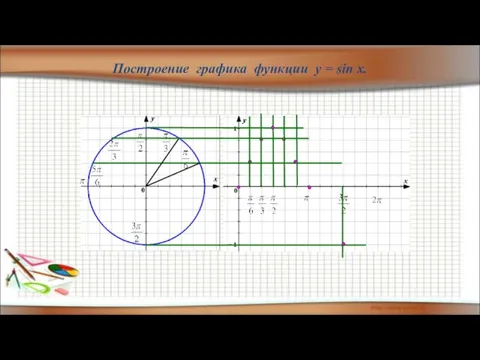
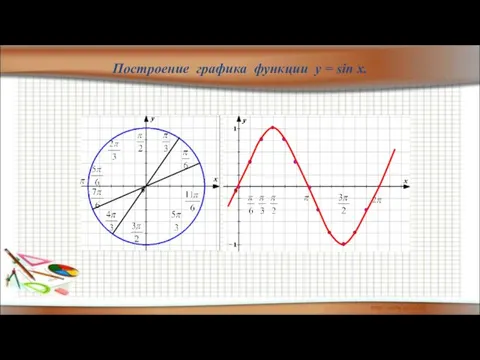
- 30. Построение графика функции y = sin x.
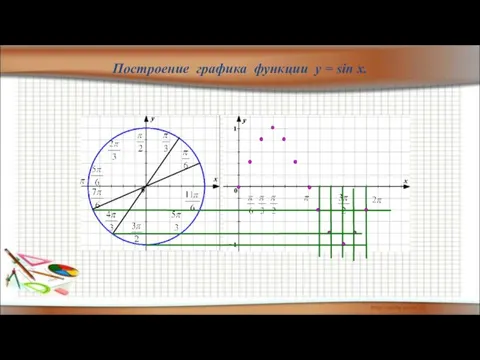
- 31. Построение графика функции y = sin x.
- 32. Построение графика функции y = sin x.
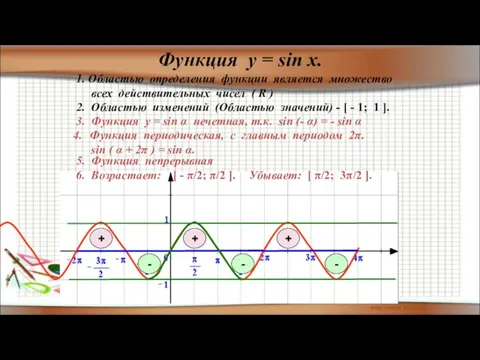
- 33. Функция у = sin x. 3. Функция у = sin α нечетная, т.к. sin (- α)
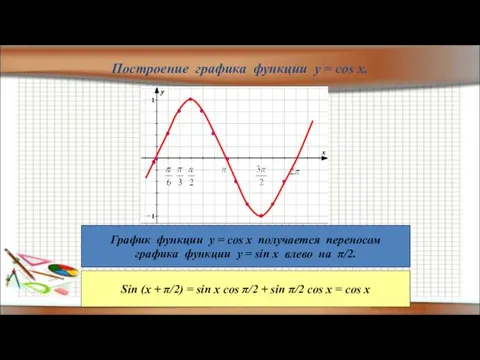
- 34. Построение графика функции y = cos x. График функции у = cos x получается переносом графика
- 36. Скачать презентацию










![Тренажер№2 Подпишите точки окружности. tϵ[0;2π]. очистить Для проверки кликни по выбранной точке](/_ipx/f_webp&q_80&fit_contain&s_1440x1080/imagesDir/jpg/55835/slide-16.jpg)
![Тренажер№3 Подпишите точки окружности. tϵ[-2π;0]. очистить Для проверки кликни по выбранной точке](/_ipx/f_webp&q_80&fit_contain&s_1440x1080/imagesDir/jpg/55835/slide-17.jpg)
![Тренажер№4 Подпишите точки окружности. tϵ[2π;4π]. очистить Для проверки кликни по выбранной точке](/_ipx/f_webp&q_80&fit_contain&s_1440x1080/imagesDir/jpg/55835/slide-18.jpg)









 Презентация Пуговка на счастье
Презентация Пуговка на счастье Изготовление заготовок ковкой
Изготовление заготовок ковкой материал для фестиваля народов мира. Русский народ
материал для фестиваля народов мира. Русский народ Дорожный контроллер ЕС-2. Эксплуатация
Дорожный контроллер ЕС-2. Эксплуатация Биосоциальная сущность личности (задания ОГЭ)
Биосоциальная сущность личности (задания ОГЭ) День православной книги
День православной книги Снаряжение для пешеходного туризма. (Тема 2)
Снаряжение для пешеходного туризма. (Тема 2) Денежные реформы России
Денежные реформы России Какую форму имеет Земля?
Какую форму имеет Земля?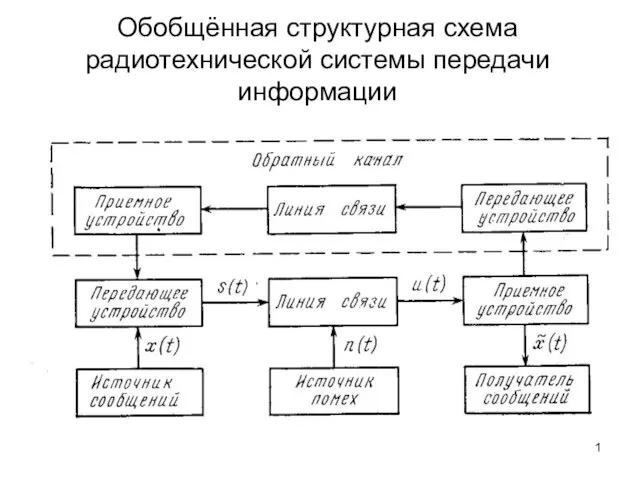 Обобщённая структурная схема радиотехнической системы передачи информации
Обобщённая структурная схема радиотехнической системы передачи информации Вторая Мировая война
Вторая Мировая война Экоурок Свобода от отходов
Экоурок Свобода от отходов Провешивание поверхностей
Провешивание поверхностей Зона транспортной инфраструктуры
Зона транспортной инфраструктуры Звуки и буквы Ч-Ть
Звуки и буквы Ч-Ть Очистка газов от пыли. Характеристики аппаратов для очистки аэрозолей
Очистка газов от пыли. Характеристики аппаратов для очистки аэрозолей Измерения параметров в процессе строительства ВОЛС. Приемо-сдаточные испытания
Измерения параметров в процессе строительства ВОЛС. Приемо-сдаточные испытания Творческая работа учащихся Выращивание кристаллов
Творческая работа учащихся Выращивание кристаллов МАС 5G. Концепции построения и развития Единой сети связи России
МАС 5G. Концепции построения и развития Единой сети связи России Оформление участка в зимнее время года
Оформление участка в зимнее время года Прикладное ПО. Инструментальное ПО
Прикладное ПО. Инструментальное ПО Профилактика психоэмоционального выгорания педагогов
Профилактика психоэмоционального выгорания педагогов Рациональное питание
Рациональное питание Иммунопатологиялық үрдістер
Иммунопатологиялық үрдістер Производство вафель
Производство вафель Разноцветные жуки. 1 класс
Разноцветные жуки. 1 класс Трикотажное полотно. Строение и свойства трикотажного полотна. Классификация трикотажных переплетений
Трикотажное полотно. Строение и свойства трикотажного полотна. Классификация трикотажных переплетений Из жизни слов. Слова добро и зло
Из жизни слов. Слова добро и зло