Содержание
- 2. Во всякой реальной колебательной системе имеются силы сопротивления, действие которых приводит к уменьшению энергии системы. В
- 3. Рассмотрим колебательную систему в которой помимо возвращающей силы имеются силы сопротивления. Запишем второй закон Ньютона для
- 4. В проекциях уравнение принимает вид: Коэффициент затухания Квадрат собственной циклической частоты
- 5. Получили дифференциальное уравнение затухающих колебаний:
- 6. Для решения однородного ДУ 2-го порядка запишем характеристическое уравнение и найдем его корни (сведения из математики):
- 8. Решением ДУ является функция вида: где А0 и ϕ0 – начальные амплитуда и начальная фаза соответственно.
- 9. Следовательно, решением ДУ является функция, описывающая зависимость координаты тела при затухающих колебаниях: где А0 и ϕ0
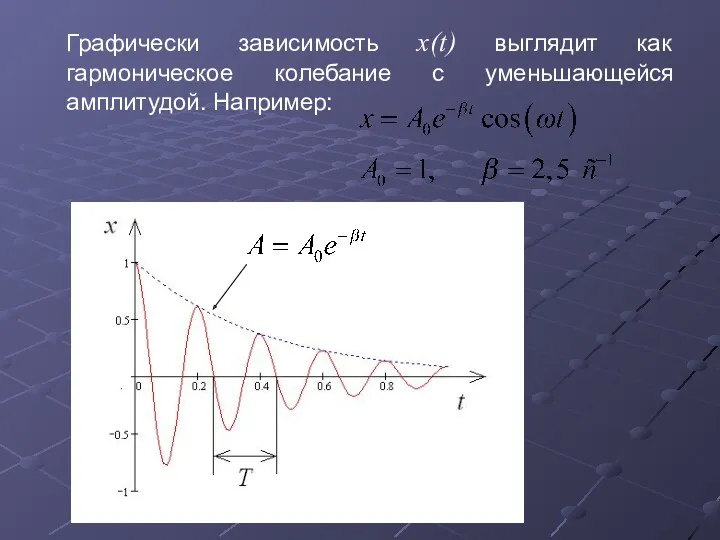
- 10. Графически зависимость x(t) выглядит как гармоническое колебание с уменьшающейся амплитудой. Например:
- 11. Циклическая частота затухающих колебаний уменьшается по сравнению с собственной частотой колебаний системы: Период колебаний увеличивается по
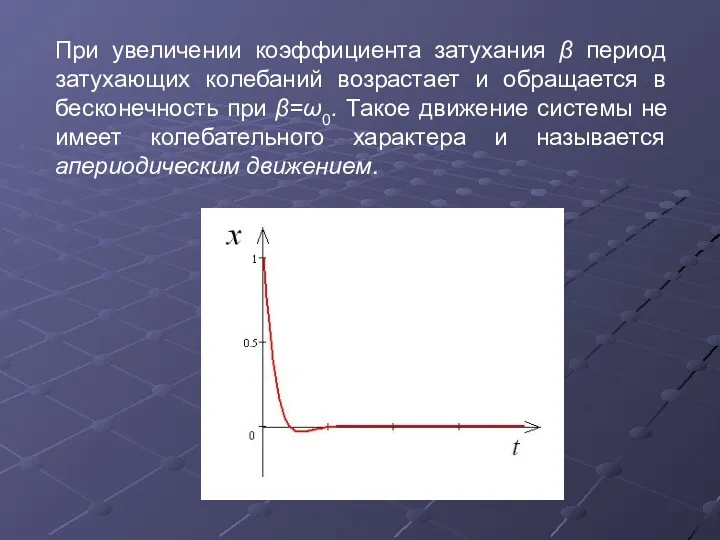
- 12. При увеличении коэффициента затухания β период затухающих колебаний возрастает и обращается в бесконечность при β=ω0. Такое
- 13. Практическое применение апериодического движения: Плавное закрытие дверей; Амортизаторы автомобилей; Успокоение колебаний стрелочных приборов (воздушные, электромагнитные демпферы).
- 14. Амплитуда колебания со временем уменьшается по экспоненциальному закону: Промежуток времени, в течение которого амплитуда колебаний уменьшается
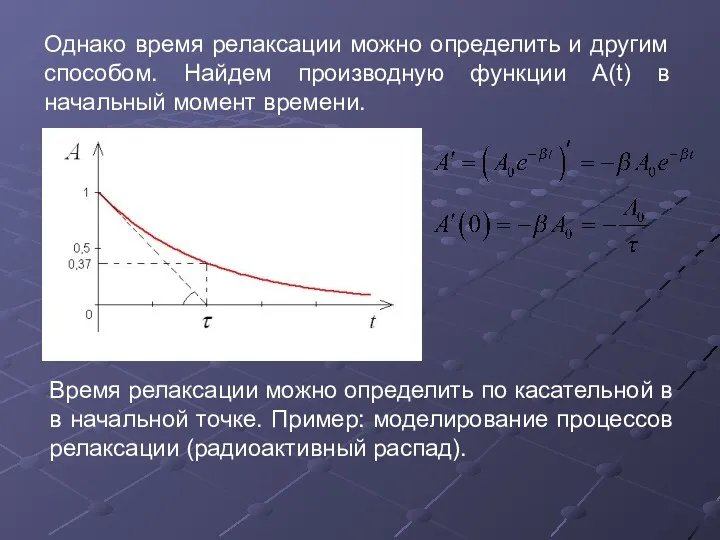
- 15. Однако время релаксации можно определить и другим способом. Найдем производную функции A(t) в начальный момент времени.
- 16. Для количественной характеристики быстроты убывания амплитуды затухающих колебаний пользуются понятиями декремента δ (отношение амплитуд через период)
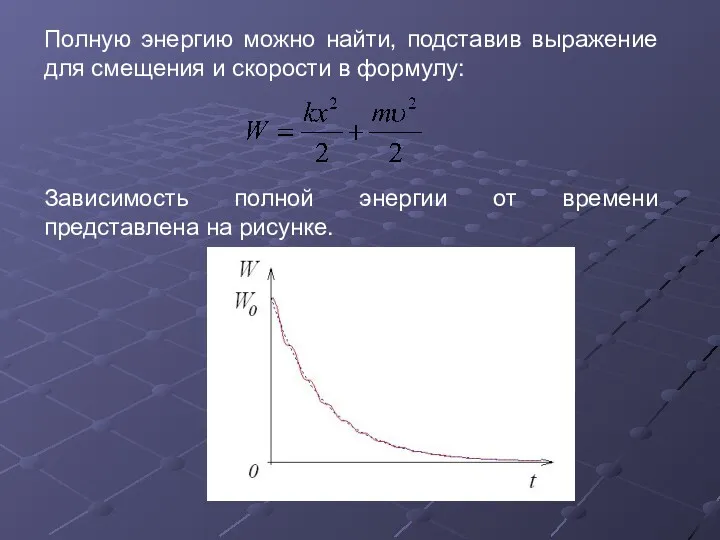
- 17. Полную энергию можно найти, подставив выражение для смещения и скорости в формулу: Зависимость полной энергии от
- 18. При малом затухании (β Полная энергия колебательной системы уменьшается со временем по экспоненциальному закону.
- 19. Добротностью Q колебательной системы называется безразмерная величина, равная произведению 2π на отношение энергии системы в произвольный
- 20. При малом затухании: Добротность пропорциональная числу колебаний за время релаксации Ne.
- 21. В ряде случаев удобно изучать колебательные процессы в системе координат (x, v). Плоскость таких координат называют
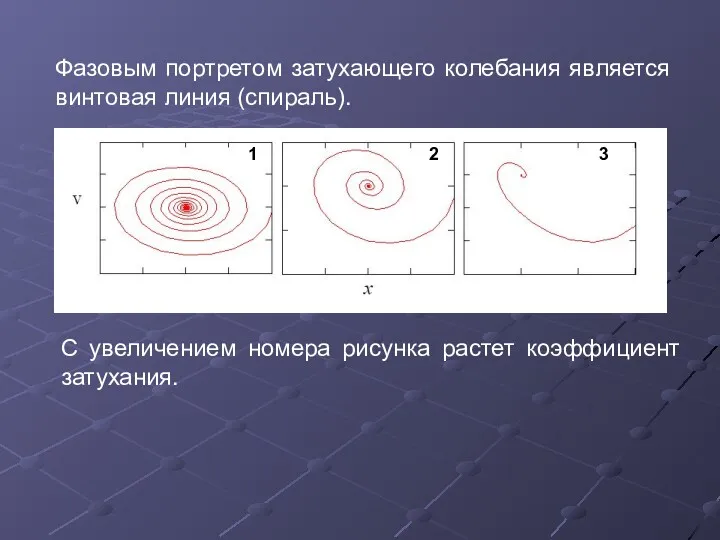
- 22. Фазовым портретом затухающего колебания является винтовая линия (спираль). 1 2 3 С увеличением номера рисунка растет
- 23. 19. Вынужденные колебания. Резонанс
- 24. Вынужденными колебаниями называются незатухающие колебания системы, которые вызываются действием на нее внешних сил, периодически изменяющихся во
- 25. В качестве модели рассмотрим тело, совершающее колебания под действием возвращающей квазиупругой силы, силы сопротивления и внешней
- 26. Преобразуя, получаем дифференциальное уравнение вынужденных колебаний (1): (1) β и ω0 – коэффициент затухания и циклическая
- 27. Решение дифференциального уравнения вынужденных колебаний равно сумме двух решений: общего и частного: Общее решение – уравнение
- 28. Подставим решение (2) в уравнение (1) и определим амплитуду и фазу между силой и смещением:
- 29. при косинусе при синусе (3) (4)
- 30. Решая совместно (3) и (4), находим амплитуду А установившихся вынужденных колебаний и сдвиг фаз межу колебаниями
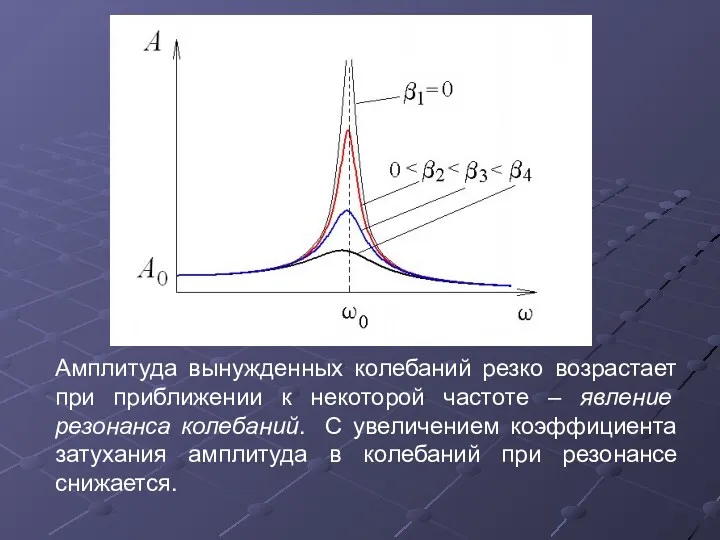
- 31. Амплитуда вынужденных колебаний резко возрастает при приближении к некоторой частоте – явление резонанса колебаний. С увеличением
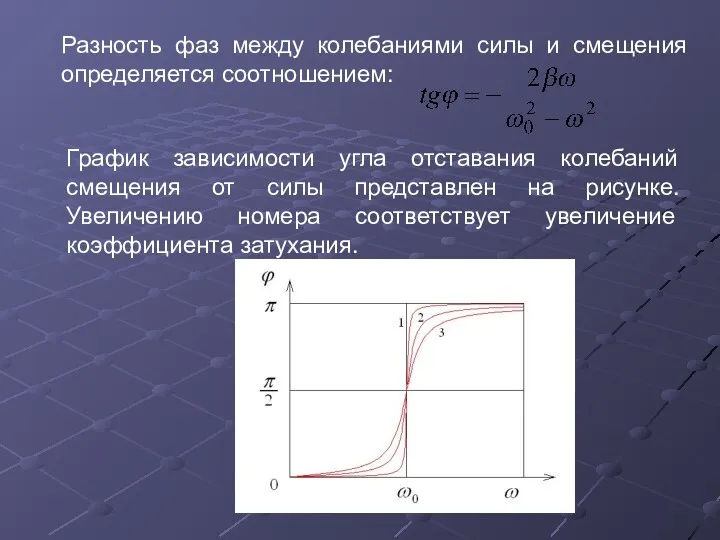
- 32. Разность фаз между колебаниями силы и смещения определяется соотношением: График зависимости угла отставания колебаний смещения от
- 33. В области малых частот амплитуда вынужденных колебаний почти постоянна, а сдвиг фаз равен нулю: В области
- 34. Для нахождения резонансной частоты для амплитуды колебаний необходимо найти максимум функции А(ω), т.е. приравнять к нулю
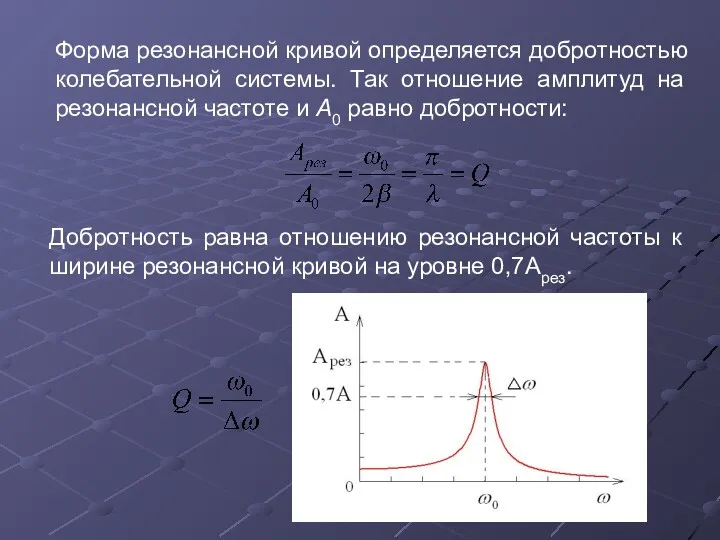
- 35. Форма резонансной кривой определяется добротностью колебательной системы. Так отношение амплитуд на резонансной частоте и A0 равно
- 36. Резонансная частота для амплитуды скорости находится аналогичным образом:
- 37. Резонансная частота для амплитуды ускорения определяется соотношением Для анализа частотной зависимости амплитуды ускорения необходимо исследовать функцию:
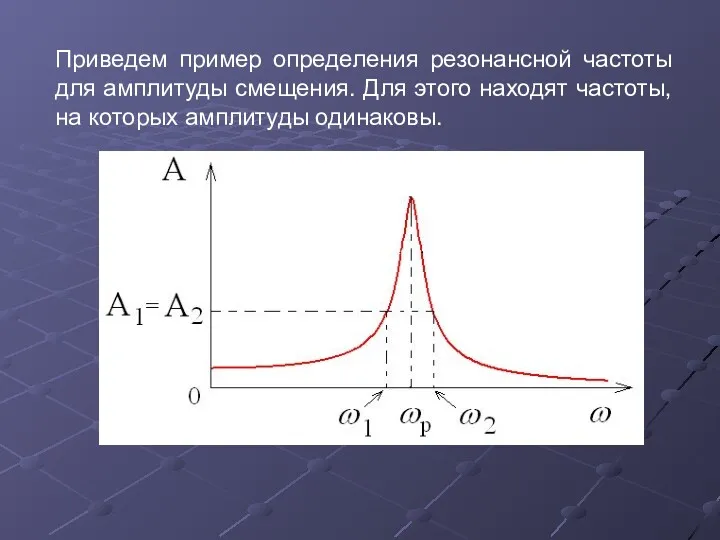
- 38. Приведем пример определения резонансной частоты для амплитуды смещения. Для этого находят частоты, на которых амплитуды одинаковы.
- 39. Вычисляют резонансную частоту.
- 40. Явление резонанса необходимо учитывать при конструировании машин и сооружений. Резонансная частота не должна быть близка к
- 41. Параметрические колебания Возбудить незатухающие колебания можно и другим способом – периодическим изменением в такт с колебаниями
- 42. В момент прохождения маятником равновесия, под действием силы уменьшается длина маятника. В результате угол отклонения увеличивается.
- 44. Скачать презентацию
































 Криминальные субкультуры
Криминальные субкультуры Образование и развитие Московского государства в XV – XVII вв. Занятие 2
Образование и развитие Московского государства в XV – XVII вв. Занятие 2 Мой профсоюз
Мой профсоюз Моя малая родина
Моя малая родина Пилотный проект Прямые выплаты
Пилотный проект Прямые выплаты Самоуплотняющийся бетон
Самоуплотняющийся бетон Известные и малоизвестные имена в краеведении Витебского края: от истоков до современности
Известные и малоизвестные имена в краеведении Витебского края: от истоков до современности Управление персоналом в социальной сфере
Управление персоналом в социальной сфере Групповые формы работы как средство реализации системно – деятельностного подхода на уроках биологии
Групповые формы работы как средство реализации системно – деятельностного подхода на уроках биологии Модель организации методической работы в муниципальном общеобразовательном учреждении Барашевская средняя общеобразовательная школа
Модель организации методической работы в муниципальном общеобразовательном учреждении Барашевская средняя общеобразовательная школа Анализ объема продаж и выявление влияния факторов на его изменение
Анализ объема продаж и выявление влияния факторов на его изменение Признаки химических реакций. Реакции обмена.
Признаки химических реакций. Реакции обмена.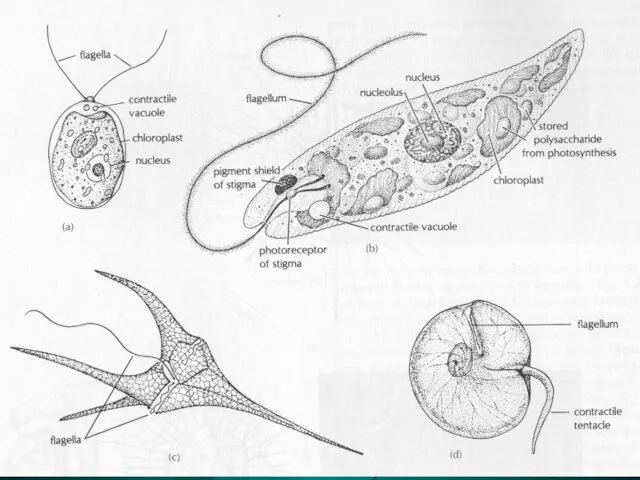 Ряд dinoflagellida. Панцирні прісноводні і морські планктонні джгутикові
Ряд dinoflagellida. Панцирні прісноводні і морські планктонні джгутикові Жилой комплекс Алатау
Жилой комплекс Алатау Международные экологические и природоохранные конференции и организации
Международные экологические и природоохранные конференции и организации Открытое занятие Берём интервью
Открытое занятие Берём интервью Гормоны
Гормоны Воспитательная компонента на уроках ИЗО и Технологии.
Воспитательная компонента на уроках ИЗО и Технологии. Наука, философия и методология науки 19 века
Наука, философия и методология науки 19 века Гломерулонефрит у детей
Гломерулонефрит у детей Сестринский процесс при хроническом энтероколите
Сестринский процесс при хроническом энтероколите Небесное и земное в звуках и красках
Небесное и земное в звуках и красках Однофазный асинхронный двигатель. Пуск и реверс однофазного асинхронного двилателя
Однофазный асинхронный двигатель. Пуск и реверс однофазного асинхронного двилателя Заглавная буква в словах
Заглавная буква в словах Металлургия редких металлов. Вольфрам. Технология производства вольфрама
Металлургия редких металлов. Вольфрам. Технология производства вольфрама Мой край . ПрезентацияЛишь в Усть-Цильме водят горку.
Мой край . ПрезентацияЛишь в Усть-Цильме водят горку. 25
25 Культура 17-18 веков
Культура 17-18 веков