Содержание
- 2. Для решения линейных и квадратных неравенств в 9 классе рассматриваются следующие приемы решения данных неравенств, данные
- 3. 1. Любой член неравенства можно перенести из одной части неравенства в другую с противоположным знаком (не
- 4. Например. Решить неравенство
- 5. Неравенство равносильно неравенству член перенесли из правой части неравенства в левую с противоположным знаком.
- 6. 2. Обе части неравенства можно умножить или разделить на одно и тоже положительное число, не меняя
- 7. Например. Решить неравенство
- 8. Неравенство равносильно Неравенству обе части первого неравенства разделили на положительное число 4
- 9. 3. Обе части неравенства можно умножить и разделить на одно и тоже отрицательное число, заменив при
- 10. Например. Решить неравенство
- 11. Неравенство равносильно Неравенству обе части первого неравенства умножили на отрицательное число -1, изменив при этом знак
- 12. Рассмотренные правила 2 и 3 допускают обобщения (соответствующие утверждения представляют собой теоремы) Теорема 1. Если обе
- 13. Например. Решить неравенство неравенство равносильно неравенству (обе части исходного неравенства умножили на выражение ( ), отрицательное
- 14. Теорема 2. Если обе части неравенства с переменной x умножить или разделить на одно и тоже
- 15. Например. Решить неравенство неравенство равносильно неравенству X+7>0 (обе части исходного неравенства разделили на выражение , положительное
- 16. Рациональные неравенства. При решении рациональных неравенств используются те приемы, которые были рассмотрены выше. С помощью этих
- 17. Метод интервалов Сущность метода интервалов заключается в следующем: ввести функцию; найти область определения; найти нули функции;
- 18. Например. Решить неравенство
- 19. Ввели функцию D (f)= R/{3} 3. Нули функции: x=1; X=-2 4-5. 6. F (x)>0 ⬄ 7.
- 20. Система неравенств Задача. Задумано натуральное число. Известно, что если к квадрату задуманного числа прибавить 13, то
- 21. Решение. Первый этап. Составление математической модели. Пусть x – задуманное число. По первому условию сумма чисел
- 23. Второй этап. Работа с составленной моделью. Преобразуем первое неравенство к виду: Найдем корни трехчлена С помощью
- 24. Преобразуем, второе неравенство системы и приведем к виду Найдем корни трехчлена С помощью параболы делаем вывод,
- 25. Третий этап. Ответ на вопрос задачи. Нас интересует натуральное число, принадлежащее интервалу (13, 15). Таким числом
- 26. Метод парабол неравенство преобразуется к виду находятся корни квадратного трехчлена x1,x2; парабола, служащая графиком функции пересекает
- 27. Например. Решить неравенство 1. 2. 3.
- 28. 4. y Ответ:
- 29. Системы уравнений Метод подстановки Суть данного метода заключается в следующем: выражается y через x из одного
- 30. Система уравнений Метод алгебраического сложения. Суть метода решения данного уравнения учащиеся рассматривается в 7 классе, где
- 32. Скачать презентацию




















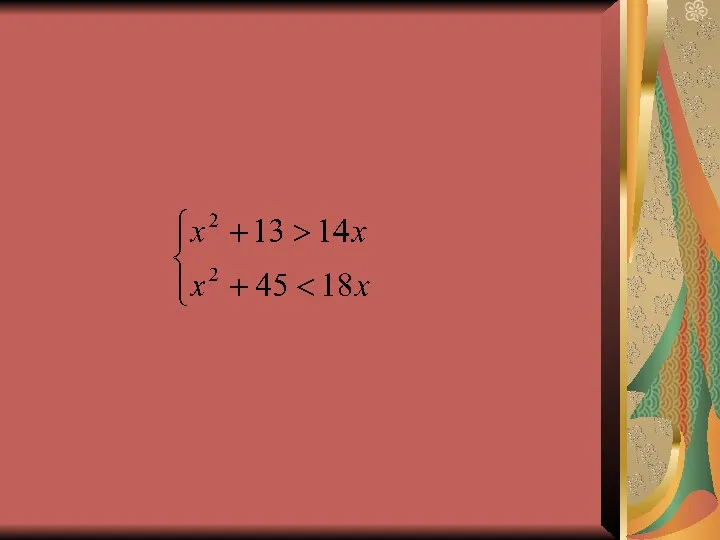








 Урок математики в 6 классе по теме: Прямая и обратная пропорциональные зависимости
Урок математики в 6 классе по теме: Прямая и обратная пропорциональные зависимости Преобразование графиков функций
Преобразование графиков функций Презентация к уроку математики в 6 классе по теме Подобные слагаемые
Презентация к уроку математики в 6 классе по теме Подобные слагаемые Обобщающий урок по теме Сложение и вычитание десятичных дробей, 5 класс
Обобщающий урок по теме Сложение и вычитание десятичных дробей, 5 класс Использование свойств функций для решения уравнений
Использование свойств функций для решения уравнений презентация и конспект урока математики 5 класс (Виленкин) Буквенная запись свойств сложения и вычитания
презентация и конспект урока математики 5 класс (Виленкин) Буквенная запись свойств сложения и вычитания Презентация к интегрированному уроку по теме: Проценты. Пропорции
Презентация к интегрированному уроку по теме: Проценты. Пропорции Кто хочет стать отличником
Кто хочет стать отличником Занятие математического кружка. Инварианты.
Занятие математического кружка. Инварианты. И это все о производной
И это все о производной Умножение одночлена на многочлен
Умножение одночлена на многочлен Урок Функции.Обобщение ЗУН и СД. Приложение.
Урок Функции.Обобщение ЗУН и СД. Приложение. Принцип Дирихле
Принцип Дирихле Презентация к уроку Методы решения тригонометрических уравнений
Презентация к уроку Методы решения тригонометрических уравнений Конспект урока по теме Сложение и вычитание дробей с разными знаменателями
Конспект урока по теме Сложение и вычитание дробей с разными знаменателями Действия с рациональными числами с использованием ИКТ
Действия с рациональными числами с использованием ИКТ Презентация к уроку на тему Подготовка к ГИА
Презентация к уроку на тему Подготовка к ГИА Презентация Площадь параллелограмма
Презентация Площадь параллелограмма Урок по теме Первообразная
Урок по теме Первообразная Решение логарифмических уравнений
Решение логарифмических уравнений Интерактивный тест по теме Функция
Интерактивный тест по теме Функция Презентация по математике на тему Степенная функция
Презентация по математике на тему Степенная функция Числовые и буквенные выражения
Числовые и буквенные выражения Математика. Подготовка к ЕГЭ - 2014. Решение заданий В9
Математика. Подготовка к ЕГЭ - 2014. Решение заданий В9 Корень n-ой степени
Корень n-ой степени Презентация для интерактивной доски Пропорции 6 класс Диск
Презентация для интерактивной доски Пропорции 6 класс Диск Презентация:Учимся решать тригонометрические неравенства
Презентация:Учимся решать тригонометрические неравенства Задания для организации итогового повторения и подготовки к итоговому тестированию по математике в 6 классе (по учебнику Виленкина)
Задания для организации итогового повторения и подготовки к итоговому тестированию по математике в 6 классе (по учебнику Виленкина)