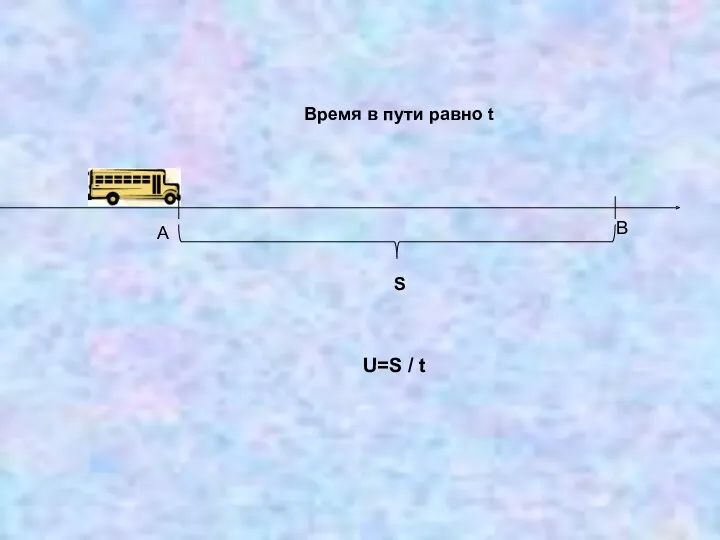
ЗАДАЧА. По прямой, на которой заданы начало отсчета, единица измерения(метр) и
наравление, движется некоторое тело (материальная точка). Закон движения задан формулой S=s(t), где t – время (в секундах), s(t) – положение тела на прямой (координата движущейся материальной точки) в момент времени t по отношению к началу отсчета (в метрах). Найти скорость движения тела в момент времени t (в м/с).
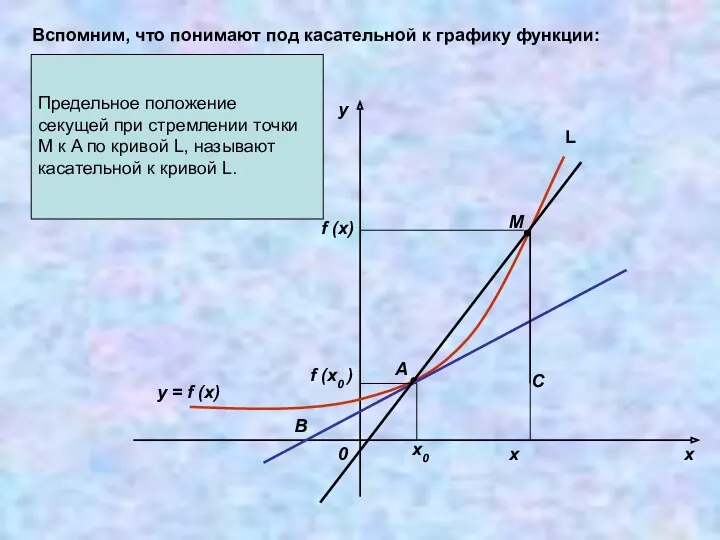
РЕШЕНИЕ. Предположим, что в момент времени t тело находилось в точке M
∆ s
M
P
O
OM=S(t). Дадим аргументу t приращение ∆t и рассмотрим ситуацию в момент времени t + ∆t . Координата материальной точки станет другой, тело в этот момент будет находиться в точке P: OP= s(t+ ∆t) – s(t).
Значит, за ∆t секунд тело переместилось из точки M в точку P.
Имеем: MP=OP – OM = s(t+ ∆t) – s(t).
Полученная разность называется приращением функции: s(t+ ∆t) – s(t)= ∆s. Итак, MP= ∆s (м).
Тогда средняя скорость на промежутке времени [t; t+∆t]:
ʋ ср= ∆s/ ∆t (м/c)








 Презентации к уроку математики
Презентации к уроку математики Частные приемы сравнения обыкновенных дробей
Частные приемы сравнения обыкновенных дробей Внеурочная деятельность Неделя Математики математическая игра Что? Где? Когда?
Внеурочная деятельность Неделя Математики математическая игра Что? Где? Когда? Делители и кратные.
Делители и кратные. Математическая викторина Своя игра
Математическая викторина Своя игра Урок Координаты на прямой
Урок Координаты на прямой основное свойство дроби
основное свойство дроби Квадратичная функция
Квадратичная функция Презентация по теме решения квадратных уравнений
Презентация по теме решения квадратных уравнений Статистические характеристики
Статистические характеристики игра для учащихся старших классов Морской бой
игра для учащихся старших классов Морской бой Урок: Классическое определение теории вероятностей
Урок: Классическое определение теории вероятностей Внеклассное мероприятие по математике для 7 класса Математика без границ!
Внеклассное мероприятие по математике для 7 класса Математика без границ! Презентация к уроку Проценты в современной жизни
Презентация к уроку Проценты в современной жизни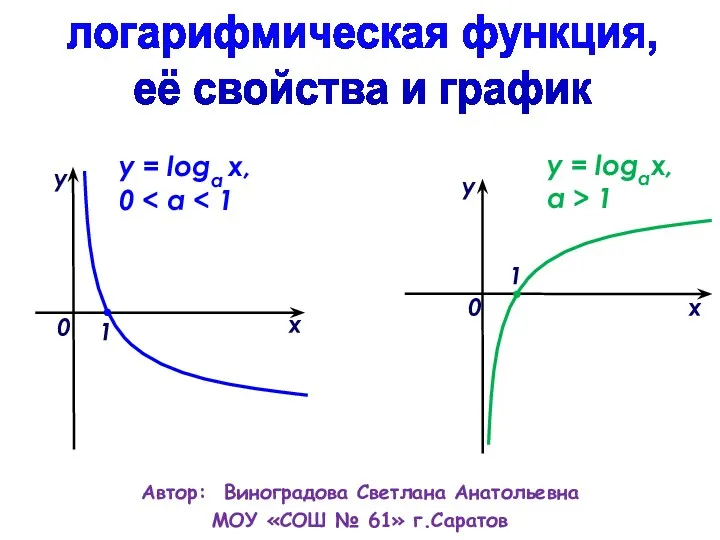 Логарифмическая функция.
Логарифмическая функция. Презентация Формулы сокращенного умножения
Презентация Формулы сокращенного умножения Квадратные уравнения
Квадратные уравнения презентация по математике для 6 класса Пропорции
презентация по математике для 6 класса Пропорции Решение задач с помощью уравнений
Решение задач с помощью уравнений ТЕМА : ЧИСЛОВЫЕ И БУКВЕННЫЕ ВЫРАЖЕНИЯ План-конспект урока по учебнику Математика 5 класс. Авторы: Н. Я. Виленкин, В. И. Жохов
ТЕМА : ЧИСЛОВЫЕ И БУКВЕННЫЕ ВЫРАЖЕНИЯ План-конспект урока по учебнику Математика 5 класс. Авторы: Н. Я. Виленкин, В. И. Жохов Презентация к уроку математики.Повторение. Занимательная математика. 6 класс
Презентация к уроку математики.Повторение. Занимательная математика. 6 класс Презентация к открытому уроку на тему: Свойства квадратного корня
Презентация к открытому уроку на тему: Свойства квадратного корня Презентация урока по теме Решение неравенств методом интервалов
Презентация урока по теме Решение неравенств методом интервалов Применение производной для исследования функции на монотонность и экстремумы.
Применение производной для исследования функции на монотонность и экстремумы. Умножение чисел с разными знаками
Умножение чисел с разными знаками урок Неравенства. 9 класс
урок Неравенства. 9 класс Презентация конкурсной работы.
Презентация конкурсной работы. Урок математики в 5 классе Деление дробей
Урок математики в 5 классе Деление дробей