Содержание
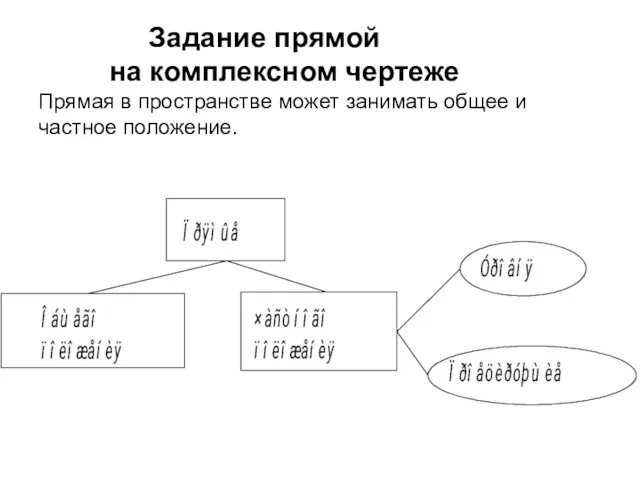
- 2. Задание прямой на комплексном чертеже Прямая в пространстве может занимать общее и частное положение.
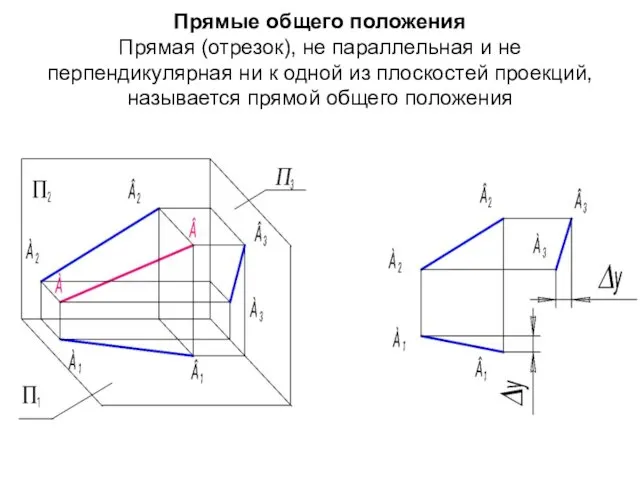
- 3. Прямые общего положения Прямая (отрезок), не параллельная и не перпендикулярная ни к одной из плоскостей проекций,
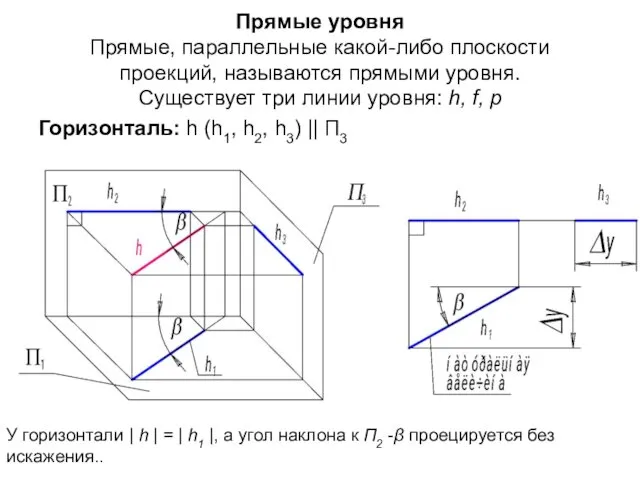
- 4. Прямые уровня Прямые, параллельные какой-либо плоскости проекций, называются прямыми уровня. Существует три линии уровня: h, f,
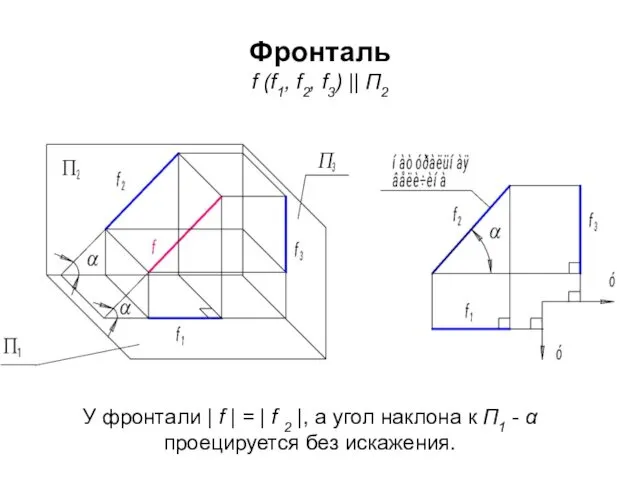
- 5. Фронталь f (f1, f2, f3) || П2 У фронтали | f | = | f 2
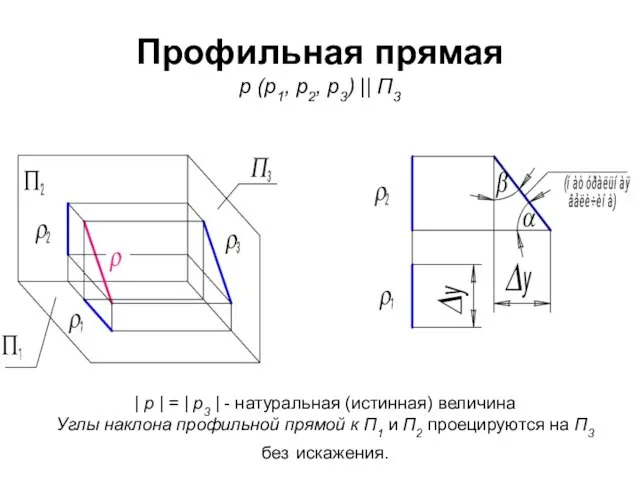
- 6. Профильная прямая р (р1, р2, р3) || П3 | p | = | p3 | -
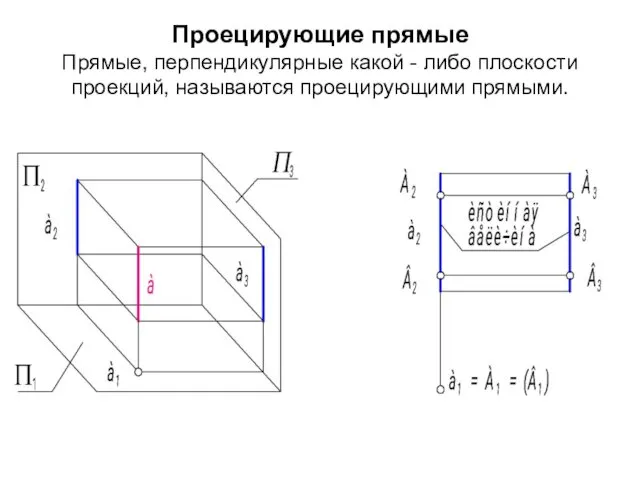
- 7. Проецирующие прямые Прямые, перпендикулярные какой - либо плоскости проекций, называются проецирующими прямыми.
- 8. Графический признак горизонтально проецирующей прямой - ее горизонтальная проекция есть точка, она называется главной проекцией Геометрическая
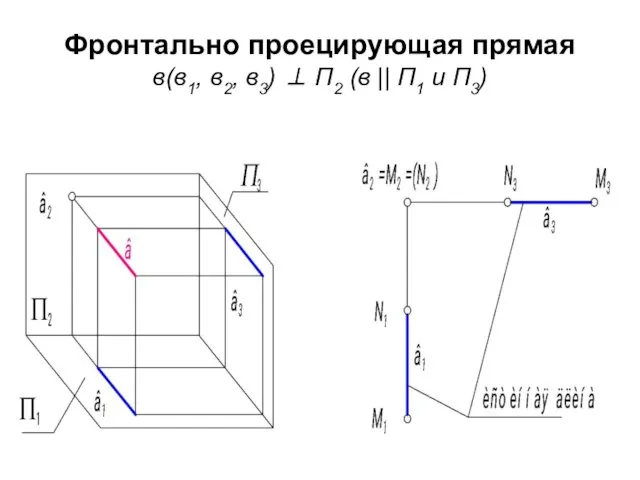
- 9. Фронтально проецирующая прямая в(в1, в2, в3) ⊥ П2 (в || П1 и П3)
- 10. Графический признак фронтально проецирующей прямой, ее фронтальная проекция есть точка, она называется главной проекцией в2 -
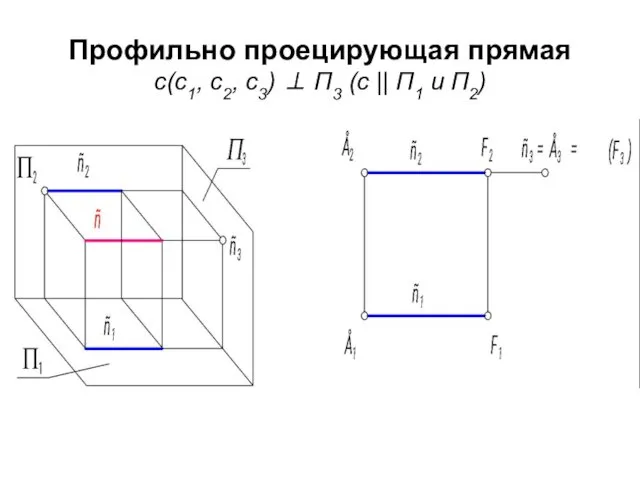
- 11. Профильно проецирующая прямая с(с1, с2, с3) ⊥ П3 (с || П1 и П2)
- 12. Графический признак профильно проецирующей прямой: ее профильная проекция есть точка, она называется главной проекцией. с3 -
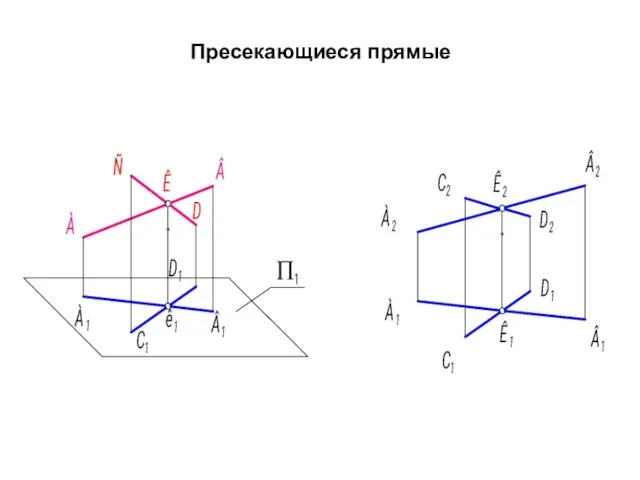
- 13. Пресекающиеся прямые
- 14. Прямые называются пересекающимися, если они имеют единственную общую точку. Они всегда лежат в одной плоскости. Если
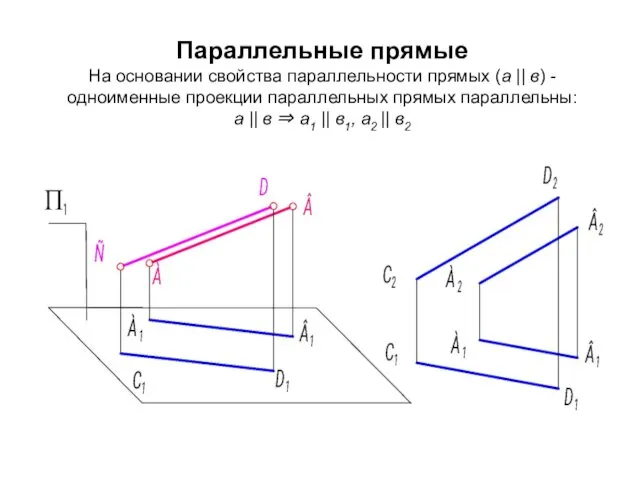
- 15. Параллельные прямые На основании свойства параллельности прямых (а || в) - одноименные проекции параллельных прямых параллельны:
- 16. Скрещивающиеся прямые Если прямые не параллельны и не пересекаются, то они называются скрещивающимися прямыми. Через скрещивающиеся
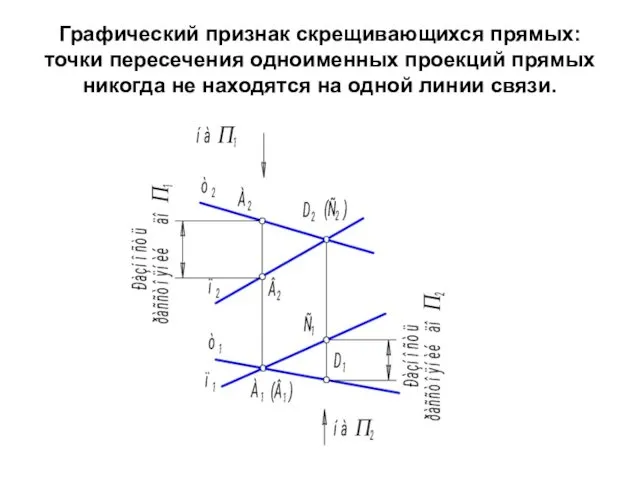
- 17. Графический признак скрещивающихся прямых: точки пересечения одноименных проекций прямых никогда не находятся на одной линии связи.
- 18. Комплексный чертеж кривых линий Если все точки кривой расположены в одной плоскости, то такую кривую называют
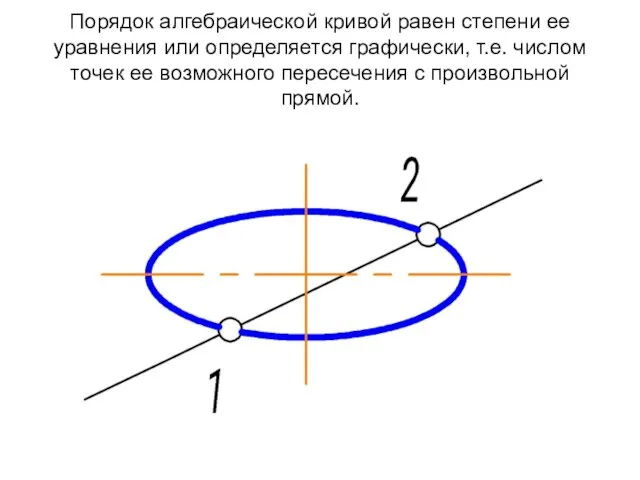
- 19. Порядок алгебраической кривой равен степени ее уравнения или определяется графически, т.е. числом точек ее возможного пересечения
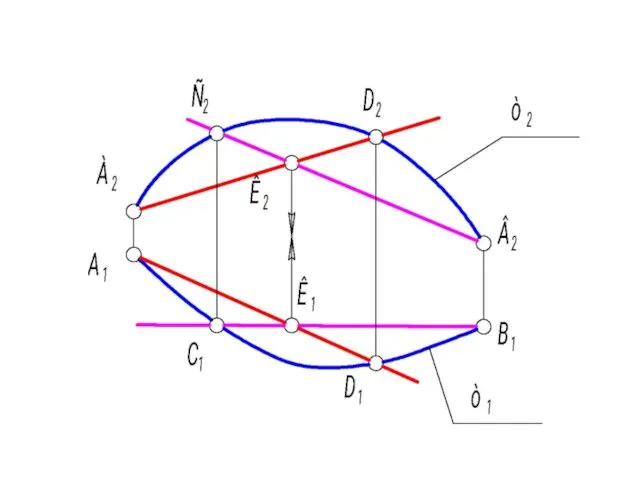
- 20. Метод хорд 1. Если хорды пересекаются (графически это видно на рис. 1-47, когда К1, К2 -
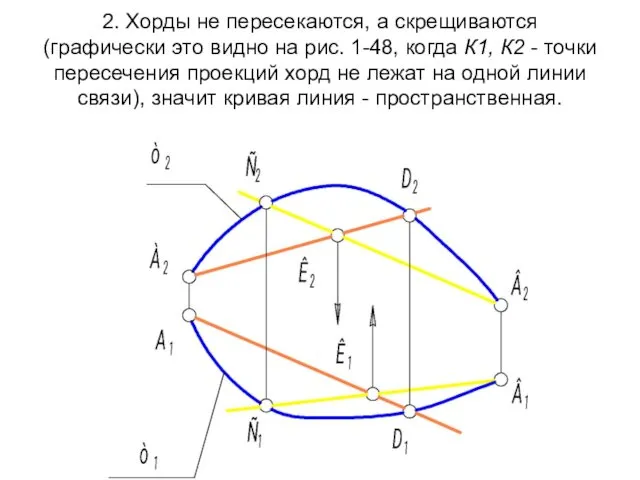
- 22. 2. Хорды не пересекаются, а скрещиваются (графически это видно на рис. 1-48, когда К1, К2 -
- 23. Свойства проекций кривых линий 1. Проекцией кривой линии является кривая линия (в общем случае). 2. Касательная
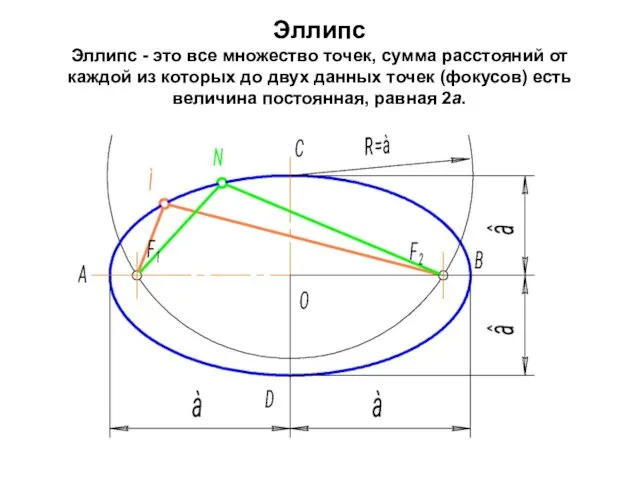
- 24. Эллипс Эллипс - это все множество точек, сумма расстояний от каждой из которых до двух данных
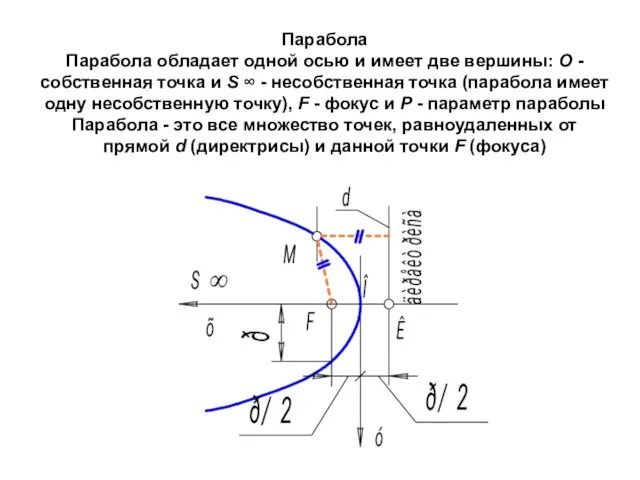
- 25. Парабола Парабола обладает одной осью и имеет две вершины: О - собственная точка и S ∞
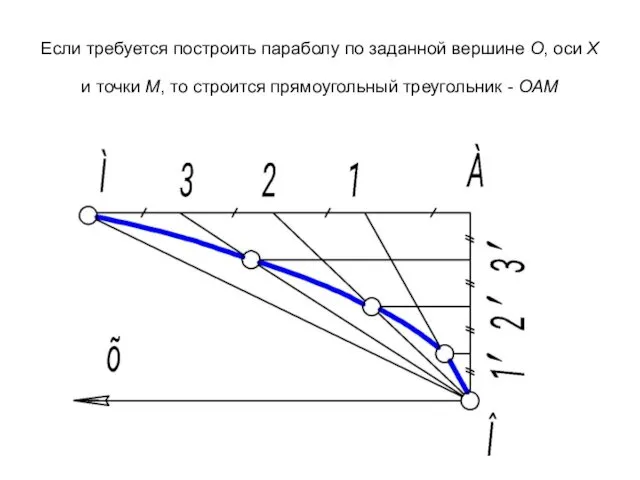
- 26. Если требуется построить параболу по заданной вершине О, оси Х и точки М, то строится прямоугольный
- 27. Гипербола - разомкнутая кривая, состоящая из двух симметричных ветвей; она имеет две оси симметрии - действительную
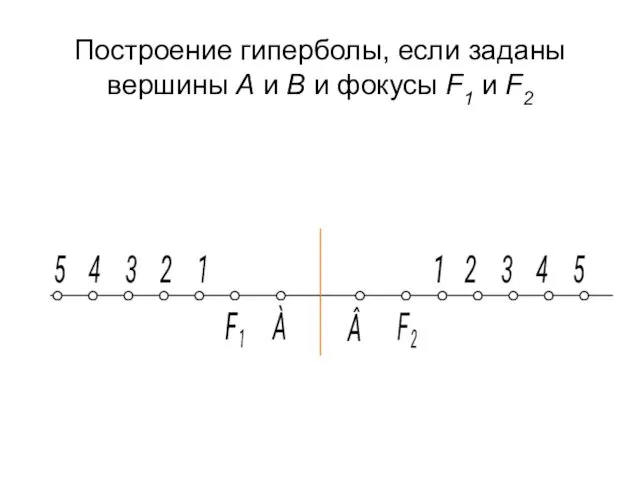
- 28. Построение гиперболы, если заданы вершины А и В и фокусы F1 и F2
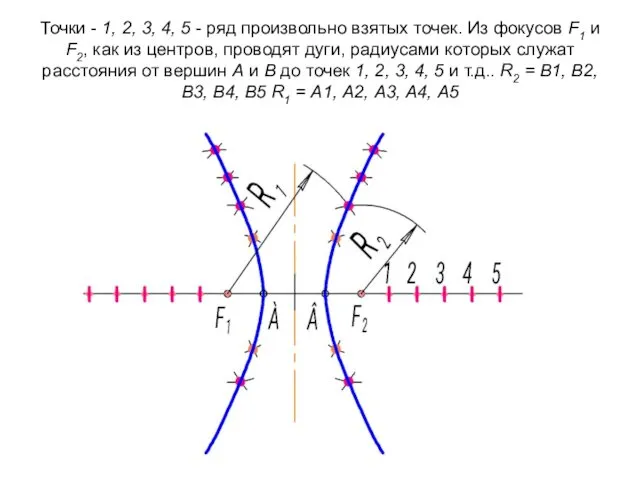
- 29. Точки - 1, 2, 3, 4, 5 - ряд произвольно взятых точек. Из фокусов F1 и
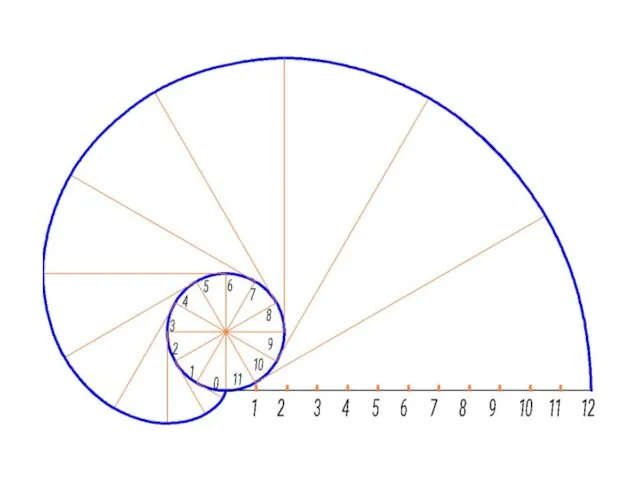
- 30. Эвольвента Эвольвента (развертка окружности)- эта лекальная кривая широко применяется в технике. Например, форма боковой поверхности зуба
- 31. Алгоритм построения 1. Окружность разделить на 12 частей. 2. В точках деления провести касательные к окружности
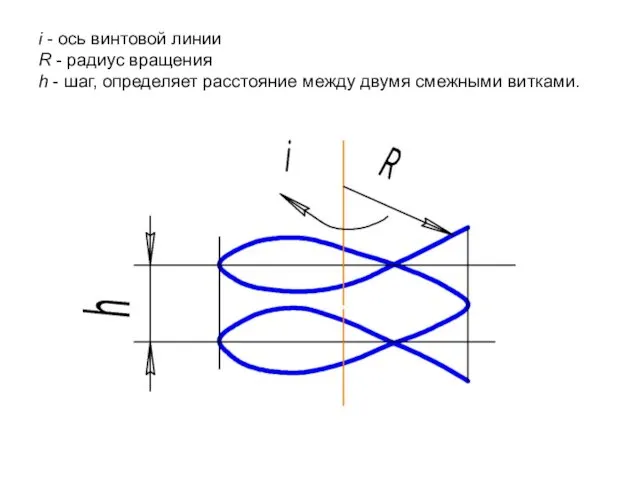
- 33. Цилиндрическая винтовая линия Цилиндрическая винтовая линия образуется вращением точки вокруг некоторой оси с одновременным поступательным движением
- 34. i - ось винтовой линии R - радиус вращения h - шаг, определяет расстояние между двумя
- 35. Алгоритм построения 1. Горизонтальную проекцию (окружность) делить на 12 частей. 2. Делить принятое значение шага (h)
- 37. Скачать презентацию













 Шероховатость поверхностей
Шероховатость поверхностей Нанесение размеров на рабочих чертежах деталей
Нанесение размеров на рабочих чертежах деталей Графическое изображение деталей и изделий
Графическое изображение деталей и изделий Сечения. Виды сечений
Сечения. Виды сечений Способы преобразования чертежа. Способ вращения вокруг прямой уровня
Способы преобразования чертежа. Способ вращения вокруг прямой уровня Поверхности. Лекция 4
Поверхности. Лекция 4 Проецирование точки. Лекция 1
Проецирование точки. Лекция 1 Графическое оформление чертежа
Графическое оформление чертежа История возникновения чертежей
История возникновения чертежей Форматы. Масштабы. Шрифты
Форматы. Масштабы. Шрифты Чертеж три вида
Чертеж три вида Аксонометрические проекции предметов, имеющих круглые поверхности
Аксонометрические проекции предметов, имеющих круглые поверхности Комплексный чертеж Три вида
Комплексный чертеж Три вида Сборочные чертежи. Разъёмные и неразъёмные соединения деталей
Сборочные чертежи. Разъёмные и неразъёмные соединения деталей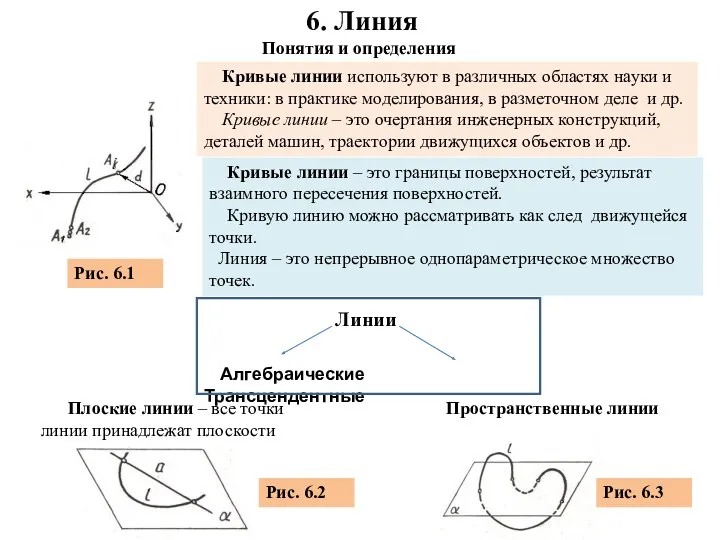 Линия. Понятия и определения
Линия. Понятия и определения Введение. Точка. Прямая. Начертательная геометрия и инженерная графика. Лекция № 1
Введение. Точка. Прямая. Начертательная геометрия и инженерная графика. Лекция № 1 Плоскость. Определить положение плоскостей к плоскостям
Плоскость. Определить положение плоскостей к плоскостям Технический рисунок. Алгоритм построения
Технический рисунок. Алгоритм построения Деталирование
Деталирование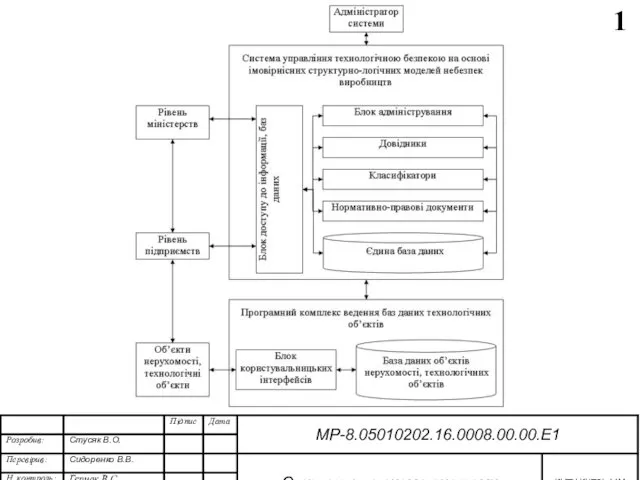 Функціональна схема системи
Функціональна схема системи Рисунок технический
Рисунок технический Метрические задачи
Метрические задачи Сборочный чертеж изделия
Сборочный чертеж изделия Инженерная графика 1 семестр
Инженерная графика 1 семестр Проектирование и монтаж станка-качалки для оборудования скважины с дебитом Q = 20 м3 /сутки и глубиной подвески насоса 1100 м
Проектирование и монтаж станка-качалки для оборудования скважины с дебитом Q = 20 м3 /сутки и глубиной подвески насоса 1100 м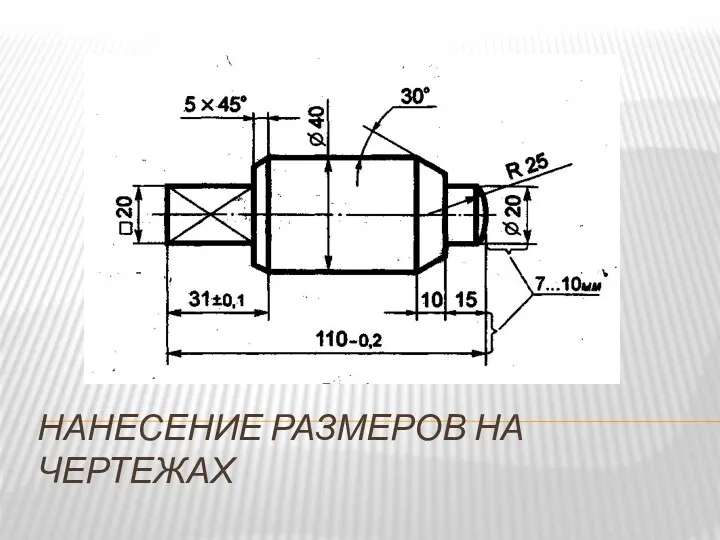 Нанесение размеров на чертежах
Нанесение размеров на чертежах Порядок чтения чертежей деталей
Порядок чтения чертежей деталей Сварные соединения
Сварные соединения