Содержание
- 2. Основоположником начертательной геометрии считается французский ученый ГАСПАР МОНЖ (1799 г. –первый учебник )
- 3. Россия впервые появились понятия: «Чертеж» - 1578 г., «Чертещик» - 1638 г. «Бок,полуширота,корпус» - эпоха Петра
- 4. Первый учебник «Основания начертательной геометрии» -1821 г.- (Я.А. Севастьянов); Впервые курс начертательной геометрии читается в учебных
- 5. «Если чертеж является языком техника, одинаково понятным всем народам, то начертательная геометрия служит грамматикой этого мирового
- 6. Приобретение необходимых знаний, умений и навыков отображать всевозможные сочетания геометрических форм трёхмерного пространства на двухмерном(плоском) носителе:
- 7. Задачи - приобрести умения и навыки графического решения типовых задач - знать основные понятия, определения и
- 8. Объект отображения Способ образования объекта отображения Элементы, формообразующие объект Носитель графической информации Способ отображения объекта Средства
- 9. МЕТОД ПРОЕКЦИЙ Лекция 1 Н.И.Красовская
- 10. Основные понятия Н.И.Красовская
- 11. Геометрическое пространство- множество точек, каждая из которых не имеет величины, но имеет определённое положение относительно выбранного
- 12. Геометрический объект (образ)- это множество точек, выделенных из пространства и подчинённых определённым условиям Н.И.Красовская
- 13. Отображение – это правило, которое устанавливает принцип однозначного соответствия точек трёхмерного пространства и вполне определённых точек
- 14. Проецирование – процесс отображения геометрических объектов трёхмерного пространства на двухмерном носителе - плоскости с помощью проецирующих
- 15. Проекция – изображение геометрического объекта, полученное в результате проецирования Н.И.Красовская
- 16. Н.И.Красовская
- 17. ТОЧКА Н.И.Красовская
- 18. Точка – 0–мерный объект Отобразить точку, значит, построить ее проекции Н.И.Красовская
- 19. Аппарат проецирования Н.И.Красовская
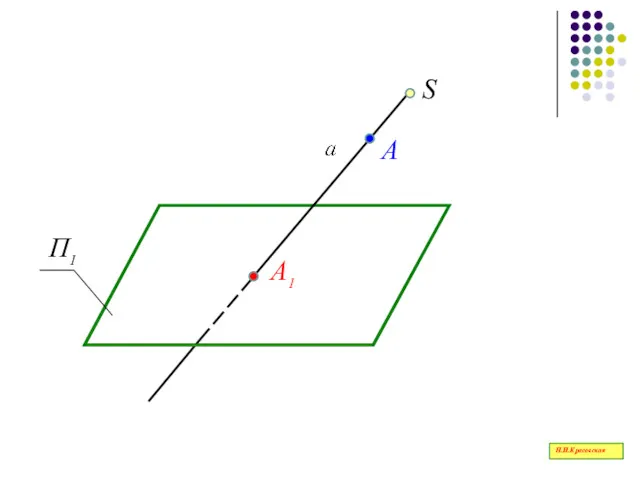
- 20. А S А1 Н.И.Красовская
- 21. - объект проецирования – (А); - плоскость проекций – (П1); - центр проецирования – ( S
- 22. Точки обозначаются прописными буквами латинского алфавита - A, B,C, D и т. д. Линии - строчными
- 23. Виды проецирования Н.И.Красовская
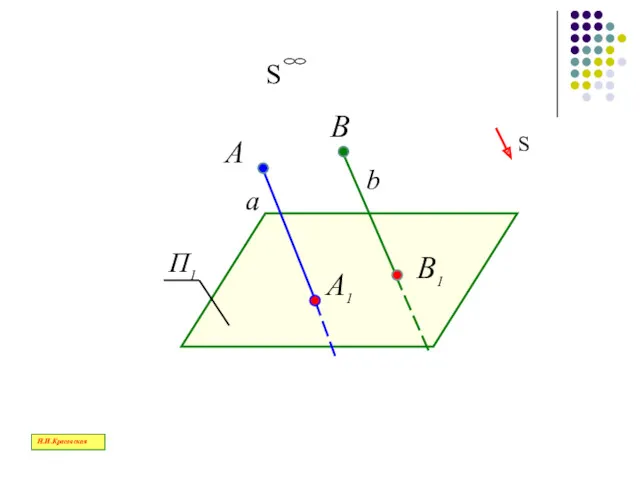
- 24. А В S А1 В1 a b Н.И.Красовская
- 25. Вид проецирования, при котором проецирующие лучи исходят из одной точки - центра проецирования, называется центральным Н.И.Красовская
- 26. Вид проецирования, при котором центр проецирования удален в бесконечность, а проецирующие лучи параллельны друг другу, называется
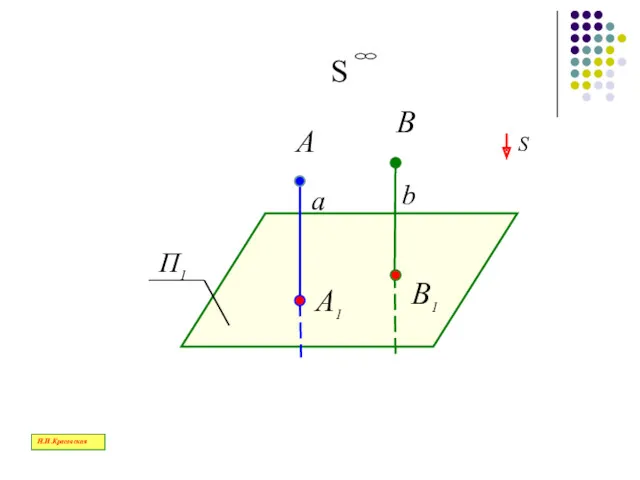
- 27. А В А1 В1 S S a b Н.И.Красовская
- 28. Вид проецирования, при котором проецирующие лучи проходят не перпендикулярно к плоскости проекций, называется косоугольным Н.И.Красовская
- 29. Вид проецирования, при котором проецирующие лучи проходят перпендикулярно плоскости проекций, называется прямоугольным или ортогональным Н.И.Красовская
- 30. А В А1 В1 S a b Н.И.Красовская
- 31. Основным видом проецирования в начертательной геометрии является ортогональный Н.И.Красовская
- 32. Основные свойства параллельного проецирования Н.И.Красовская
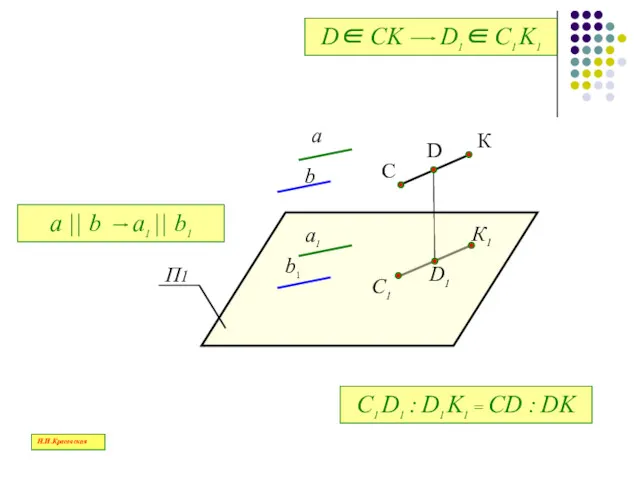
- 33. 4. Отношение отрезков проекции прямой равно отношению отрезков прямой в пространстве 2. Проекции параллельных прямых параллельны
- 34. П1 a b a1 b1 D С К С1 К1 D1 С1 D1 : D1 K1
- 35. Обратимость чертежа. Координаты точки. Комплексный чертеж точки Н.И.Красовская
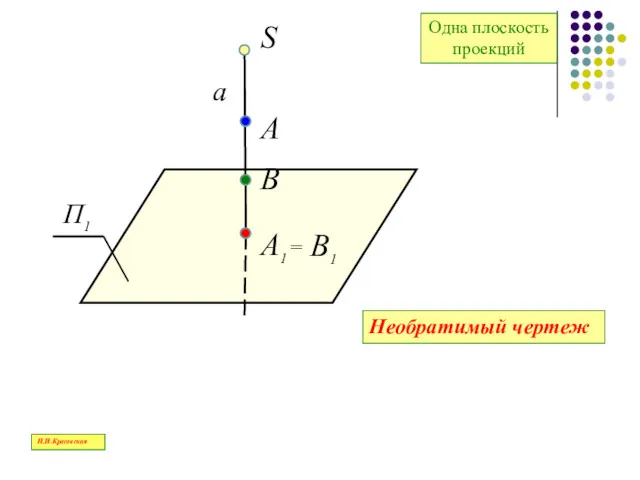
- 36. Обратимый чертеж – это чертеж, позволяющий однозначно определять форму, размеры и положение предмета в пространстве Н.И.Красовская
- 37. П1 S А В В1 А1 a = Необратимый чертеж Одна плоскость проекций Н.И.Красовская
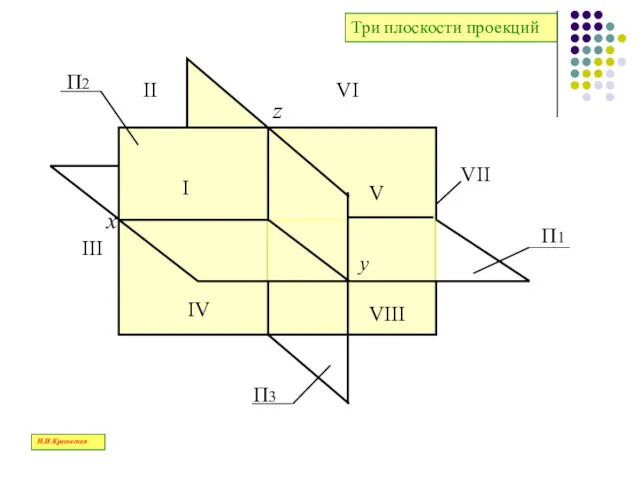
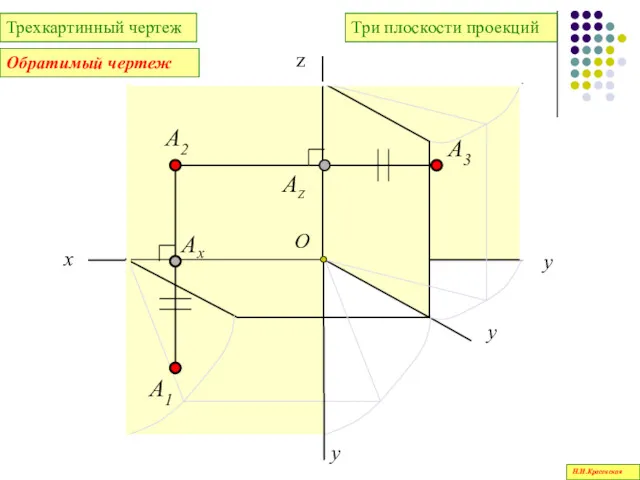
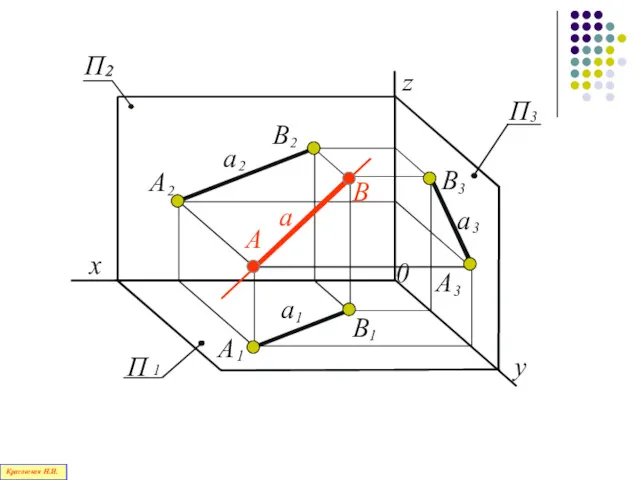
- 38. Три плоскости проекций Н.И.Красовская
- 39. Линия пересечения П1 и П2 – ось Х, линия пересечения П2 и П3 – ось Z,
- 40. Координатой точки называется расстояние от точки до плоскости проекций Н.И.Красовская
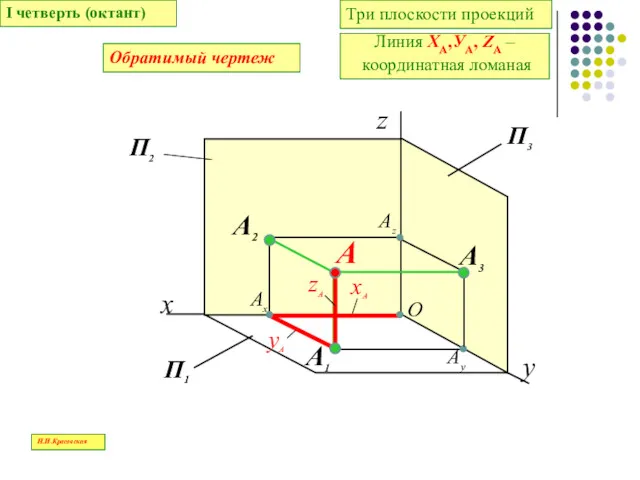
- 41. I четверть (октант) z у х П1 П2 П3 А А2 Ах А1 Ау Аz А3
- 42. Z- расстояние от точки до плоскости проекций П1- высота точки Х - расстояние от точки до
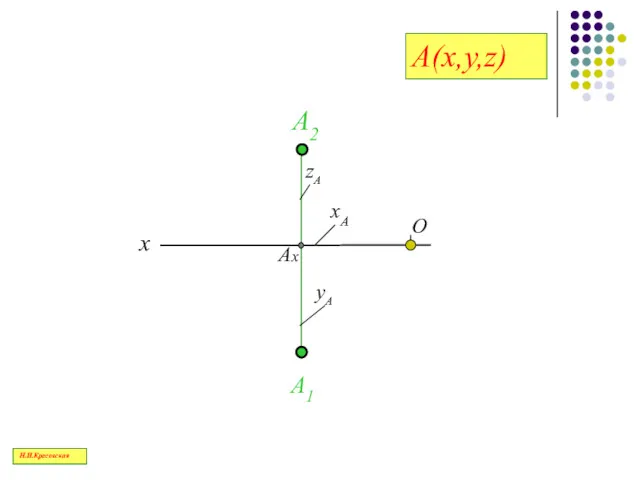
- 43. Координаты измеряются в миллиметрах и записываются в следующем порядке: Х,У, Z, например, А(30,20,10) Н.И.Красовская
- 44. Для удобства плоскости проекций разворачивают и совмещают с фронтальной плоскостью проекций Получается комплексный чертеж - эпюр
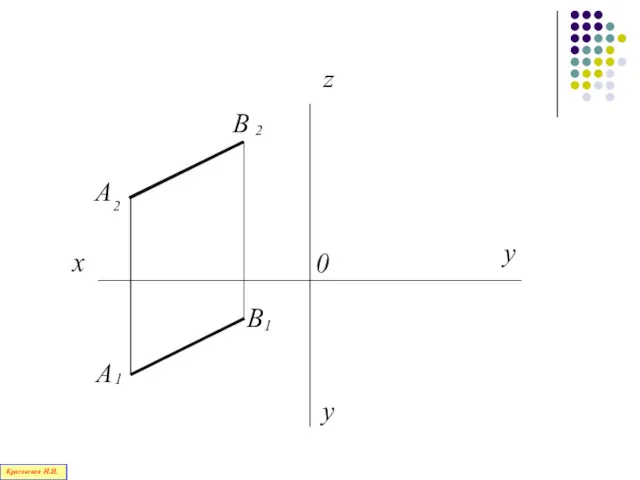
- 45. Три плоскости проекций Обратимый чертеж Трехкартинный чертеж у х z О у у Н.И.Красовская
- 46. Ось У раздваивается, но расстояния по обеим осям всегда равны!!! Н.И.Красовская
- 47. Пространство является трехмерным Любая проекция определяется двумя координатами, поэтому она является двумерной Н.И.Красовская
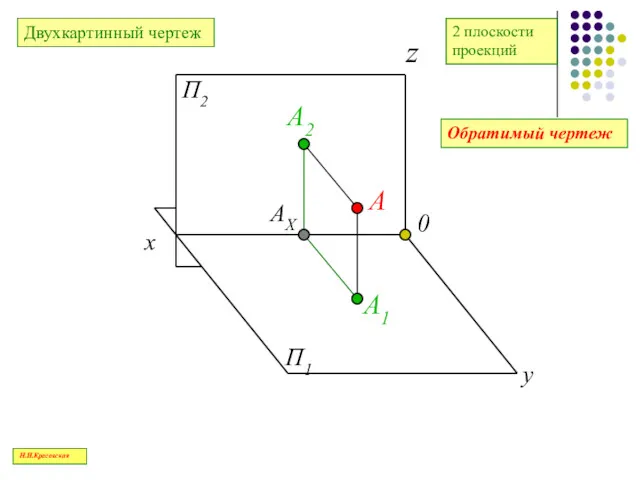
- 48. П1 П2 x 0 АX А2 А А1 y z 2 плоскости проекций Обратимый чертеж Двухкартинный
- 49. A(x,y,z) Ах х О А1 А2 zA yA xA Н.И.Красовская
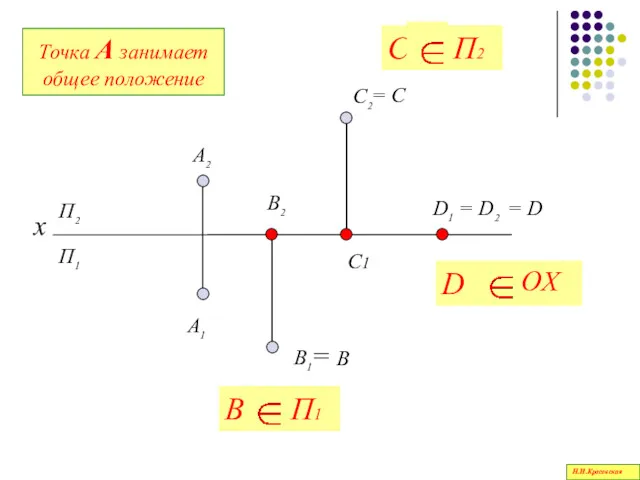
- 50. Точки общего и частного положения Н.И.Красовская
- 51. П1 П2 х А2 А1 В1 В2 С1 С2 D1 = D2 = В = С
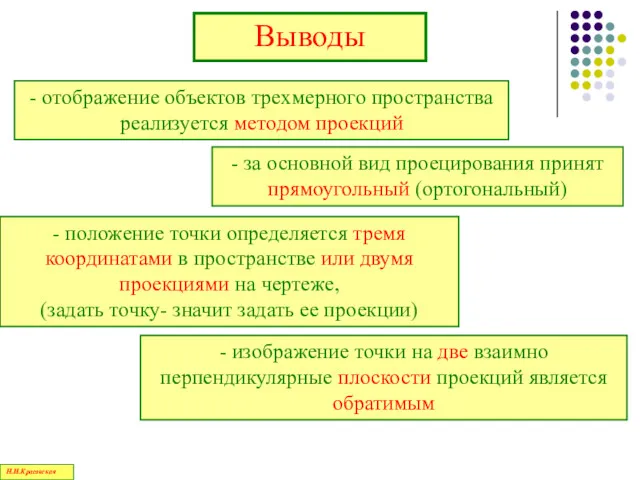
- 52. Выводы - отображение объектов трехмерного пространства реализуется методом проекций - за основной вид проецирования принят прямоугольный
- 53. Л И Н И И Лекция 2 Красовская Н.И.
- 54. Линия – это множество положений непрерывно движущейся в пространстве точки Линия – это одномерный геометрический объект
- 55. Прямая линия Красовская Н.И.
- 56. Простейшей линией является прямая линия Прямая получается при непрерывном движении точки без изменения ее направления Прямая
- 57. Задание прямой линии на чертеже. Определитель прямой Красовская Н.И.
- 58. Совокупность элементов, задающих прямую в пространстве, называется ее определителем Красовская Н.И.
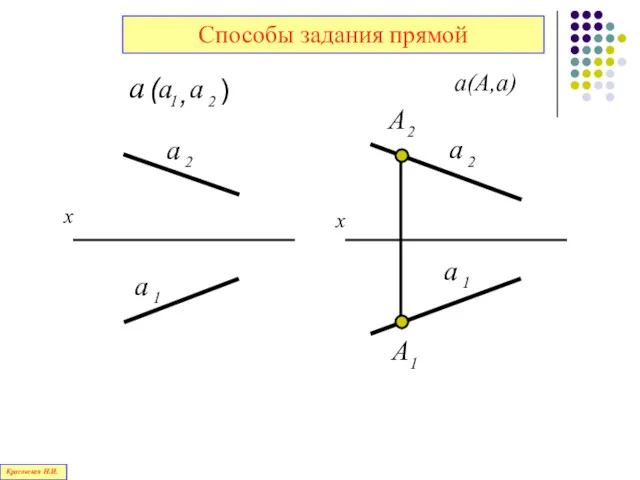
- 59. а(А,В) а([АВ]) Способы задания прямой Красовская Н.И.
- 60. а(А,а) Способы задания прямой Красовская Н.И.
- 61. Положение прямой линии в пространстве Красовская Н.И.
- 62. Прямая в пространстве может занимать два положения: общее и частное Красовская Н.И.
- 63. Прямые общего положения Красовская Н.И.
- 64. Прямые, не параллельные и не перпендикулярные ни одной из плоскостей проекций, называются прямыми общего положения Красовская
- 65. Красовская Н.И.
- 66. Красовская Н.И.
- 67. Прямые частного положения Красовская Н.И.
- 68. Прямые, параллельные или перпендикулярные одной из плоскостей проекций, называются прямыми частного положения Красовская Н.И.
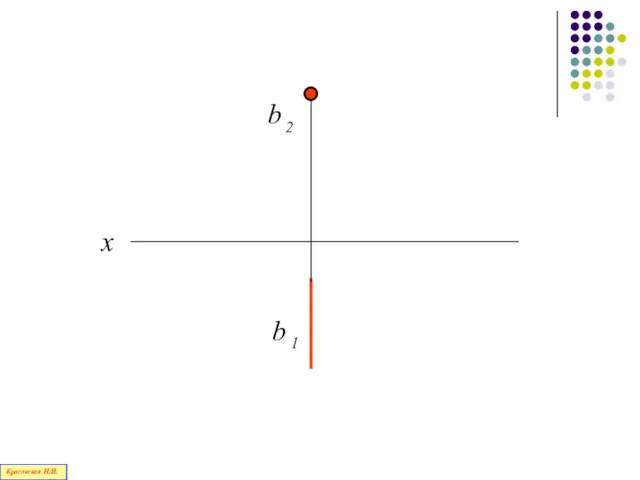
- 69. Прямые уровня Красовская Н.И.
- 70. Прямые, параллельные одной из плоскостей проекций, называются прямыми уровня Красовская Н.И.
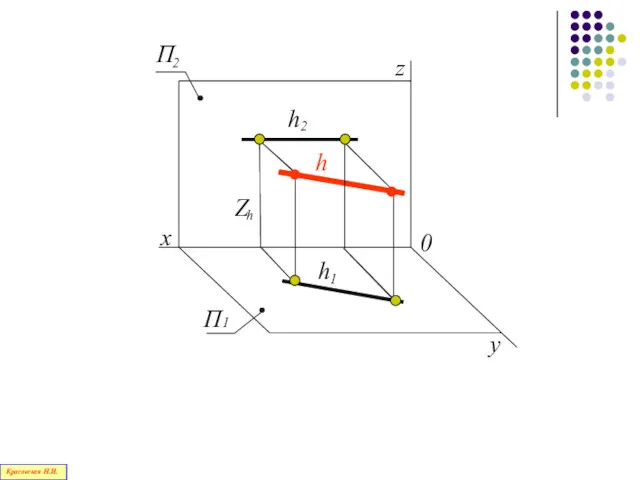
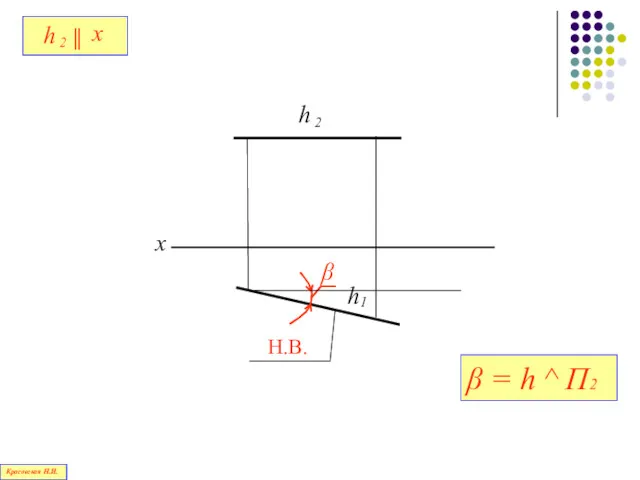
- 71. Прямая, параллельная горизонтальной плоскости проекций П1, называется горизонталью Красовская Н.И.
- 72. h Z h Красовская Н.И.
- 73. x Н.В. β = h ^ П2 Красовская Н.И.
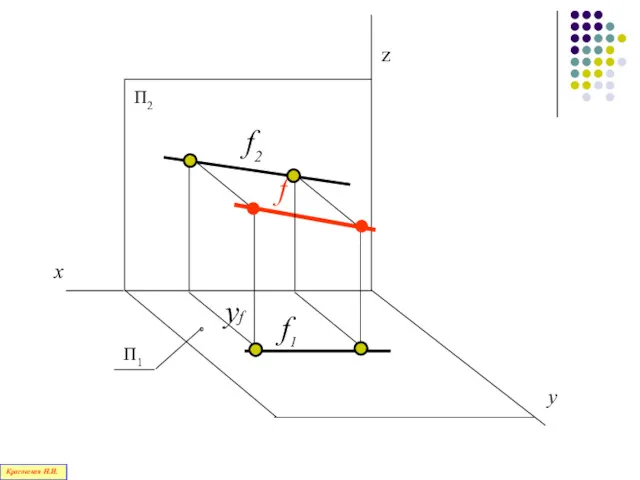
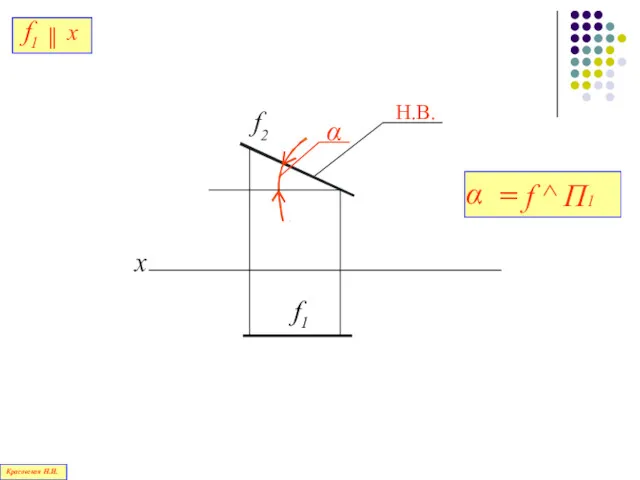
- 74. Прямая, параллельная фронтальной плоскости проекций П2, называется фронталью Красовская Н.И.
- 75. х f2 f f1 yf Красовская Н.И.
- 76. x Н.В. Красовская Н.И.
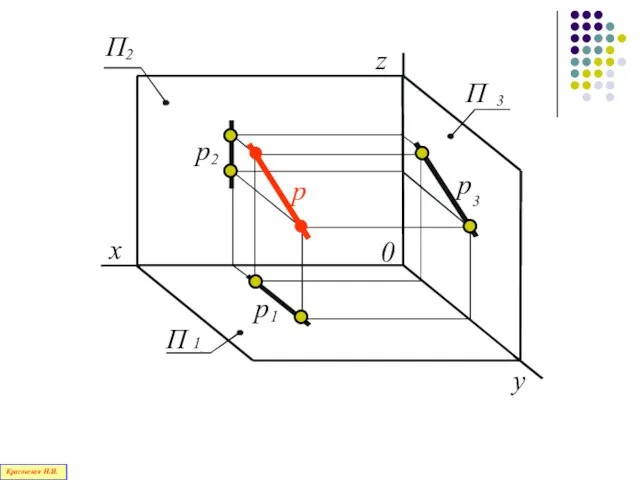
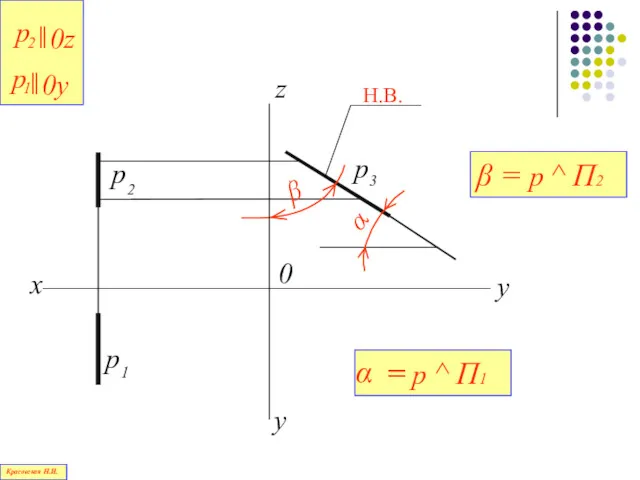
- 77. Прямая, параллельная профильной плоскости проекций П3, называется профильной прямой Красовская Н.И.
- 78. Красовская Н.И.
- 79. 0 y x z y Н.В. β = p ^ П2 Красовская Н.И.
- 80. Проецирующие прямые Красовская Н.И.
- 81. Прямые, перпендикулярные одной из плоскостей проекций, называются проецирующими Красовская Н.И.
- 82. Прямая, перпендикулярная горизонтальной плоскости проекций П1 – горизонтально - проецирующая прямая Красовская Н.И.
- 83. a Красовская Н.И.
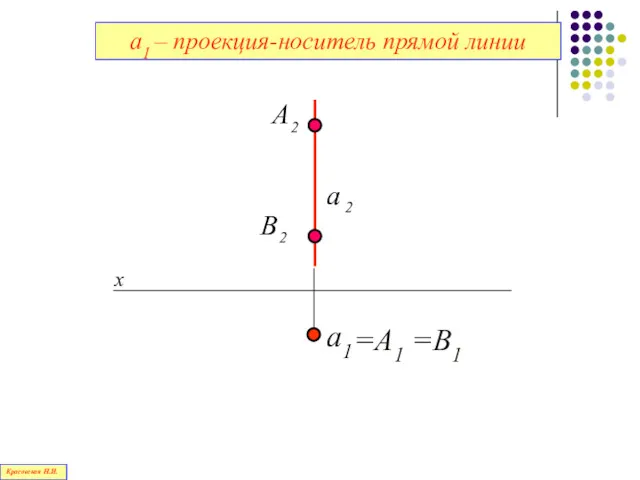
- 84. а1 – проекция-носитель прямой линии a1 =A1 =B1 Красовская Н.И.
- 85. Проекция-носитель обладает собирательным свойством: все точки, лежащие на проецирующей прямой, проецируются в эту проекцию-носитель Красовская Н.И.
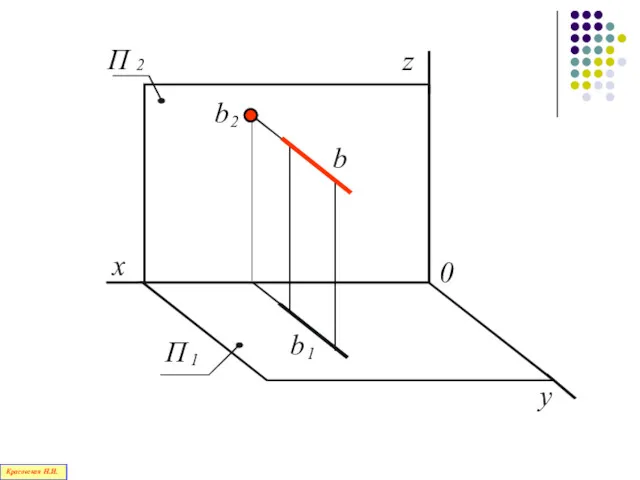
- 86. Прямая, перпендикулярная фронтальной плоскости проекций П2– фронтально - проецирующая прямая Красовская Н.И.
- 87. b Красовская Н.И.
- 88. х Красовская Н.И.
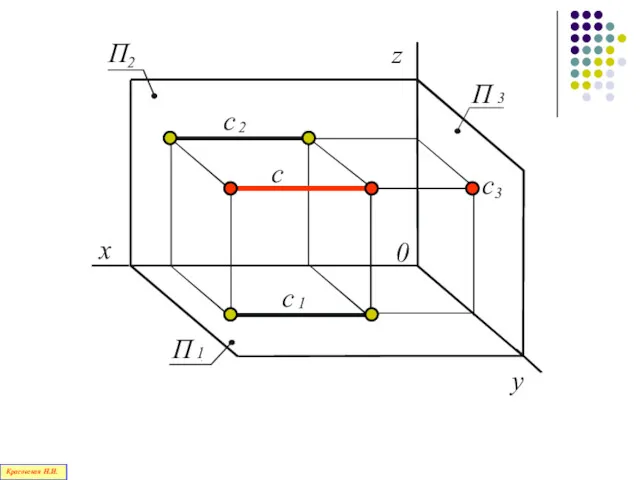
- 89. Прямая, перпендикулярная профильной плоскости проекций П3 – профильно - проецирующая прямая Красовская Н.И.
- 90. П 2 z 3 1 x 0 y П П Красовская Н.И.
- 91. х z y o C2 C1 C3 y Красовская Н.И.
- 92. Точка на прямой Красовская Н.И.
- 93. Если точка в пространстве лежит на прямой, то ее проекции лежат на соответствующих проекциях этой прямой
- 94. x А 1 B 1 Красовская Н.И.
- 95. Взаимное положение прямых Красовская Н.И.
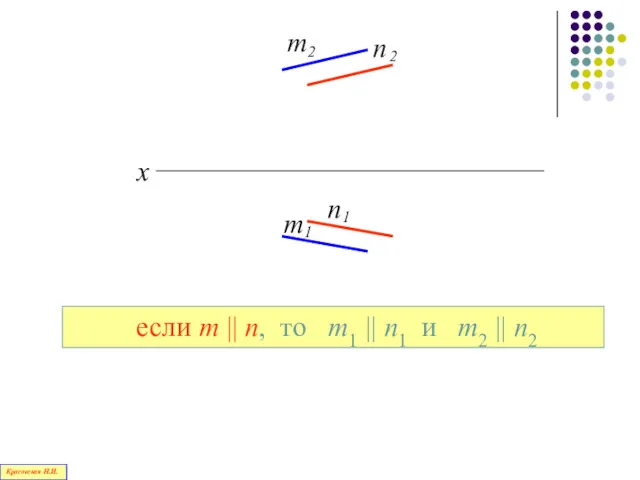
- 96. Проекции параллельных прямых параллельны Красовская Н.И.
- 97. x если m || n, то m1 || n1 и m2 || n2 Красовская Н.И.
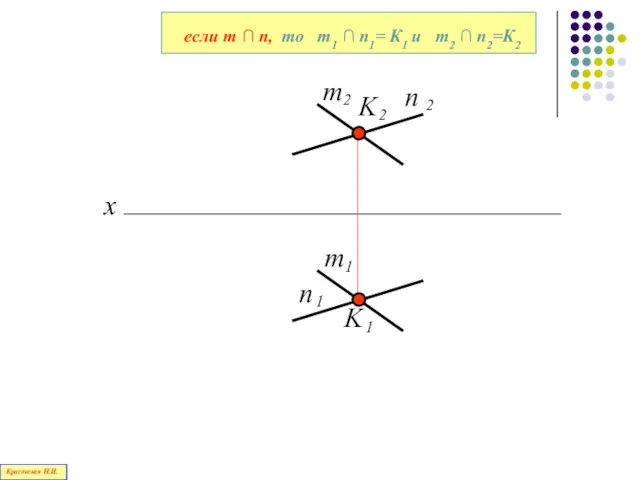
- 98. Прямые линии, имеющие общую точку, называются пересекающимися Красовская Н.И.
- 99. x если m ∩ n, то m1 ∩ n1= К1 и m2 ∩ n2=К2 Красовская Н.И.
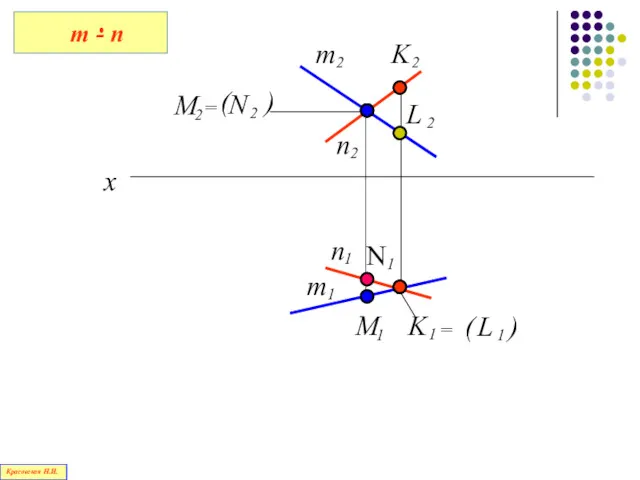
- 100. Не пересекающиеся и не параллельные между собой прямые, называются скрещивающимися Красовская Н.И.
- 101. Точки пересечения проекций скрещивающихся прямых являются проекциями двух разных точек этих прямых в пространстве Эти точки
- 102. = = N 2 ( ) ( ) x Красовская Н.И.
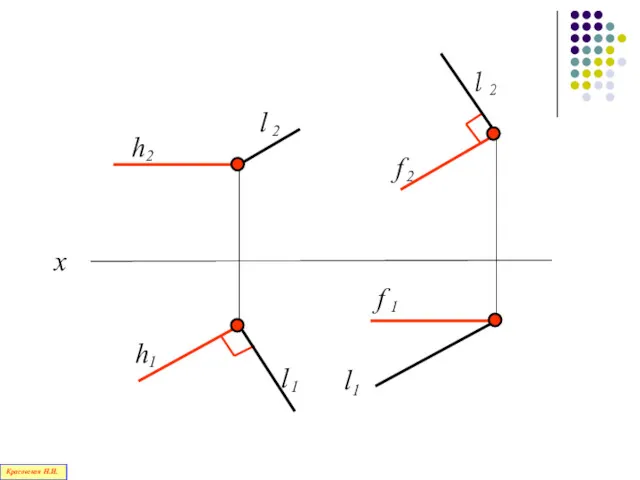
- 103. Теорема о проекциях прямого угла Красовская Н.И.
- 104. Если одна сторона прямого угла параллельна плоскости проекций, а другая ей не перпендикулярна, то прямой угол
- 105. x Красовская Н.И.
- 106. Прямой угол можно построить на чертеже без искажения только с натуральной величиной прямой уровня Красовская Н.И.
- 107. Кривые линии Красовская Н.И.
- 108. Кривая линия получается при движении точки с изменением направления Красовская Н.И.
- 109. Циркульные кривые линии - линии, кривизна которых постоянна Закономерные кривые - это линии, закон образования которых
- 110. Плоские кривые линии Красовская Н.И.
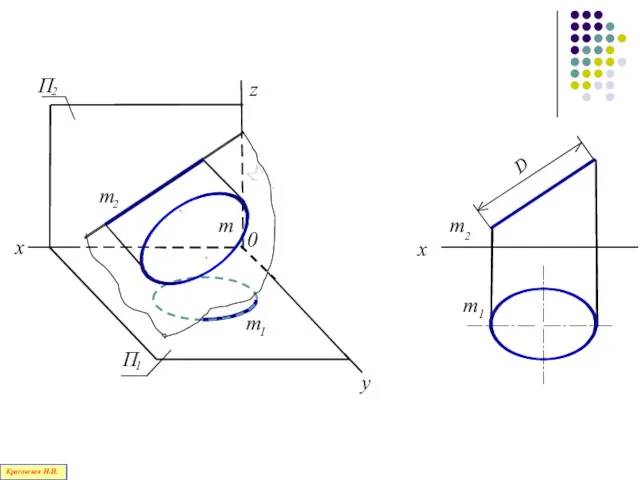
- 111. Кривые линии, все точки которых принадлежат одной плоскости, называются плоскими Красовская Н.И.
- 112. х у z O D Красовская Н.И.
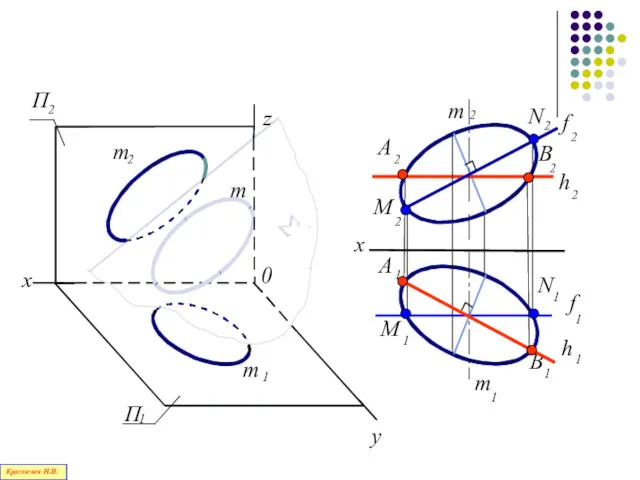
- 113. y 2 П 1 x z 0 x 1 m m m 2 m 2 1
- 114. Большие оси эллипсов принадлежат линиям уровня, (соответственно горизонтали h и фронтали f ), и по величине
- 115. 0 П 2 1 y x z m 1 m 2 m П A N h
- 116. Пространственные кривые Красовская Н.И.
- 117. Кривые линии, все точки которых не принадлежат одной плоскости, называются пространственными Красовская Н.И.
- 118. Чтобы определить длину кривой линии, необходимо осуществить ее спрямление Красовская Н.И.
- 119. Винтовые линии Красовская Н.И.
- 120. Винтовая линия представляет собой траекторию движения точки, равномерно вращающейся вокруг оси и одновременно перемещающейся с постоянной
- 121. Шаг винтовой линии – это величина перемещения точки в направлении оси, соответствующая одному обороту ее вокруг
- 122. левой, если точка перемещается от наблюдателя, вращаясь против часовой стрелки правой, если точка перемещается к наблюдателю,
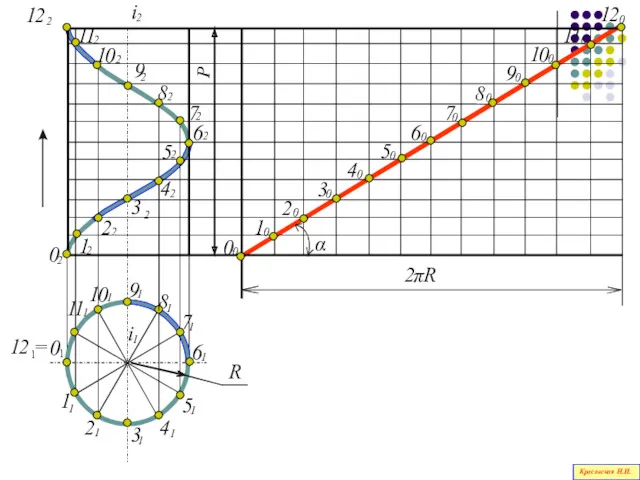
- 123. На развертке цилиндрической поверхности винтовая линия изображается прямой, являющейся гипотенузой прямоугольного треугольника, у которого один катет
- 124. i 2 i 1 R 2 π R 1 2 3 4 5 6 7 8
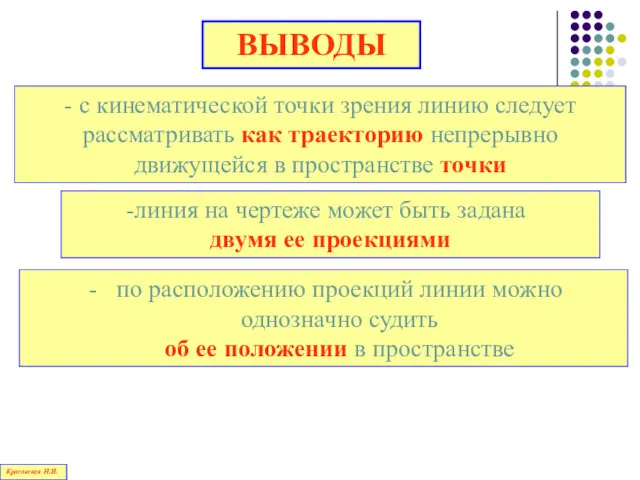
- 125. по расположению проекций линии можно однозначно судить об ее положении в пространстве ВЫВОДЫ - с кинематической
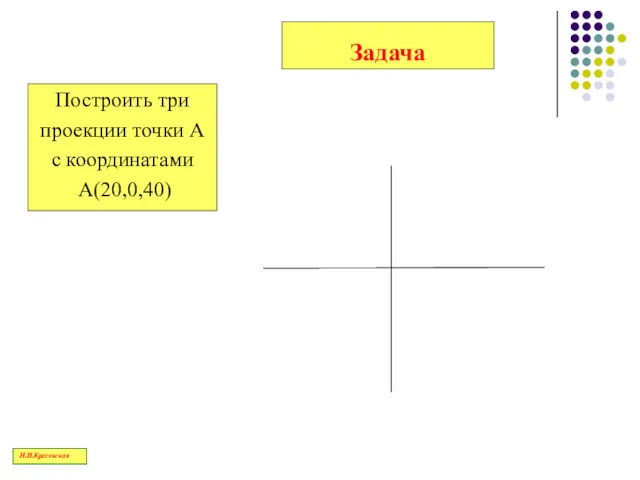
- 126. Задача Построить три проекции точки А с координатами А(20,0,40) Н.И.Красовская
- 128. Скачать презентацию












































![а(А,В) а([АВ]) Способы задания прямой Красовская Н.И.](/_ipx/f_webp&q_80&fit_contain&s_1440x1080/imagesDir/jpg/148775/slide-58.jpg)













































 Чтение сборочных чертежей
Чтение сборочных чертежей Построение проекций плоских фигур
Построение проекций плоских фигур Технический рисунок. Алгоритм построения
Технический рисунок. Алгоритм построения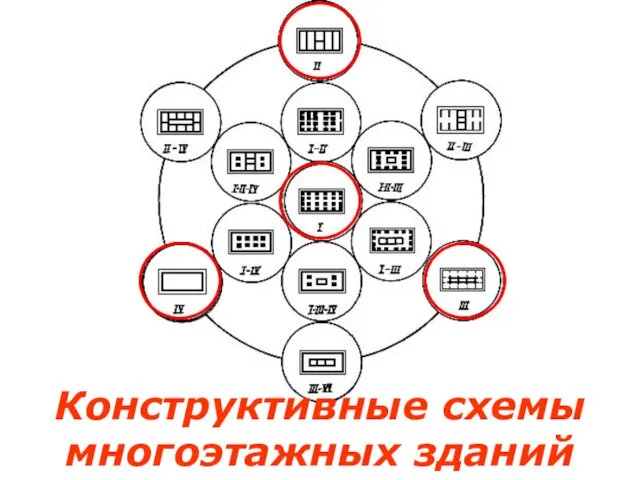 Конструктивные схемы многоэтажных зданий
Конструктивные схемы многоэтажных зданий Сызбаны безендіру ережелері (пішім,масштаб,негізгі жазу)
Сызбаны безендіру ережелері (пішім,масштаб,негізгі жазу) Сопряжения
Сопряжения Сечения. Виды, изображение и обозначение сечений
Сечения. Виды, изображение и обозначение сечений Комплексный чертёж плоскости и поверхности
Комплексный чертёж плоскости и поверхности Комплект чертежей дифференциальной установки
Комплект чертежей дифференциальной установки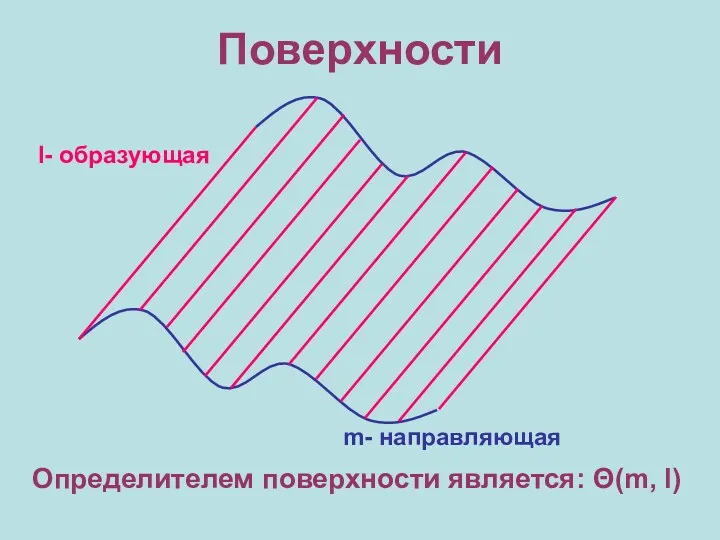 Поверхности. Лекция №4
Поверхности. Лекция №4 Линии чертежа
Линии чертежа Перспектива. Построение объектов
Перспектива. Построение объектов План строительства торгового центра Зельгрос Кэш энд Керри
План строительства торгового центра Зельгрос Кэш энд Керри Inzhenrnaya_grafika_Soedinenie_detaley
Inzhenrnaya_grafika_Soedinenie_detaley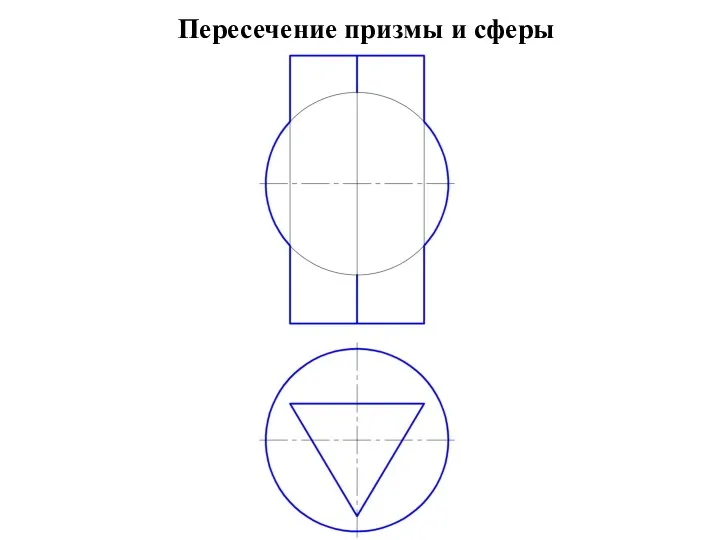 Пересечение призмы и сферы
Пересечение призмы и сферы Черчение. Начальные сведения
Черчение. Начальные сведения Аксонометрические проекции. Урок 1
Аксонометрические проекции. Урок 1 Сечения и разрезы деталей на чертеже
Сечения и разрезы деталей на чертеже Проекция точки на одну плоскость. Эпюр Монжа в системе трех плоскостей проекций
Проекция точки на одну плоскость. Эпюр Монжа в системе трех плоскостей проекций Начертательная геометрия и инженерная графика. Развертки. Лекция 14
Начертательная геометрия и инженерная графика. Развертки. Лекция 14 Сборочные чертежи
Сборочные чертежи Оформление плана землевладения, землепользования
Оформление плана землевладения, землепользования Соединения деталей
Соединения деталей Соединение деталей. Разъемные и неразъемные соединения. Резьба
Соединение деталей. Разъемные и неразъемные соединения. Резьба Виды соединений
Виды соединений Модели и моделирование
Модели и моделирование Конструкторско-технологическая подготовка производства модернизации привода главного движения станка модели 1к62
Конструкторско-технологическая подготовка производства модернизации привода главного движения станка модели 1к62 Загальні правила оформлення креслеників. Види. Лекція 1
Загальні правила оформлення креслеників. Види. Лекція 1