Содержание
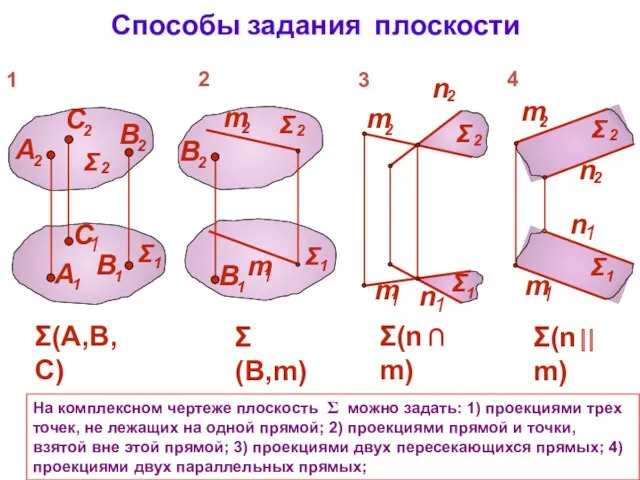
- 2. Способы задания плоскости На комплексном чертеже плоскость Σ можно задать: 1) проекциями трех точек, не лежащих
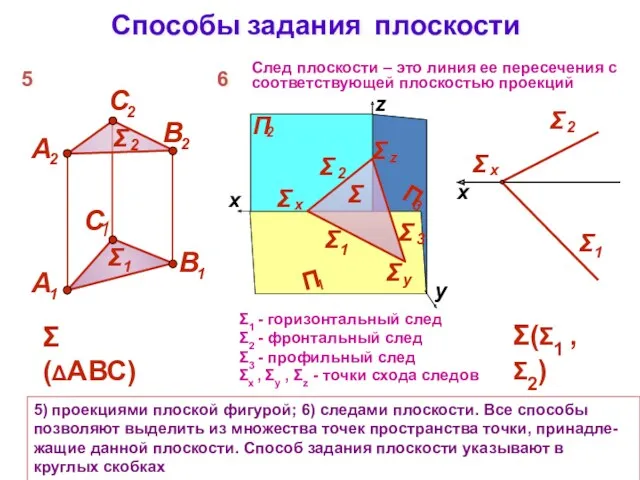
- 3. Способы задания плоскости 5) проекциями плоской фигурой; 6) следами плоскости. Все способы позволяют выделить из множества
- 4. Положение плоскости относительно плоскостей проекций Плоскость общего положения наклонена ко всем плоскостям проекций Плоскость частного положения
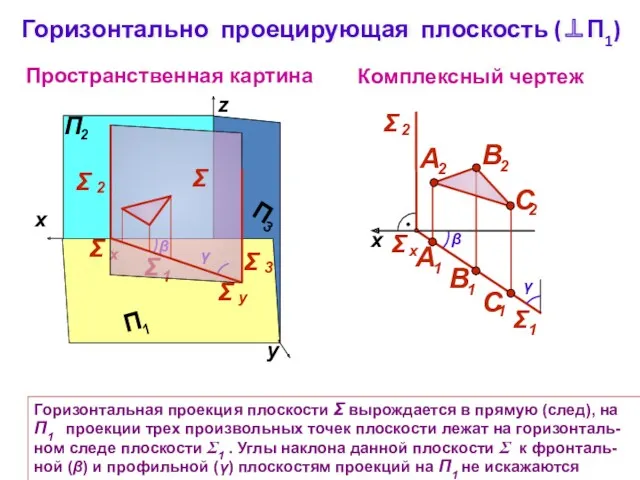
- 5. Горизонтально проецирующая плоскость (⊥П1) Пространственная картина Комплексный чертеж y z Горизонтальная проекция плоскости Σ вырождается в
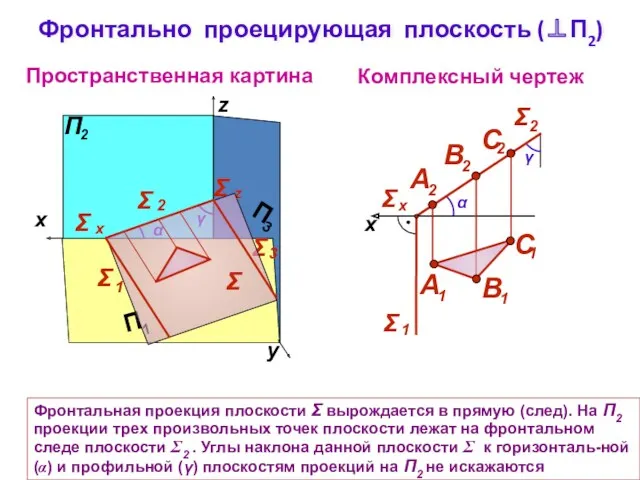
- 6. Фронтально проецирующая плоскость (⊥П2) Комплексный чертеж y z Пространственная картина γ α Σ Фронтальная проекция плоскости
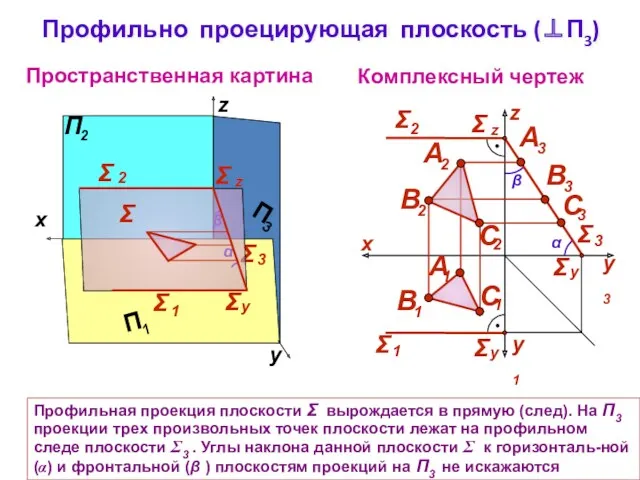
- 7. Профильно проецирующая плоскость (⊥П3) Комплексный чертеж z Пространственная картина α β Σ Профильная проекция плоскости Σ
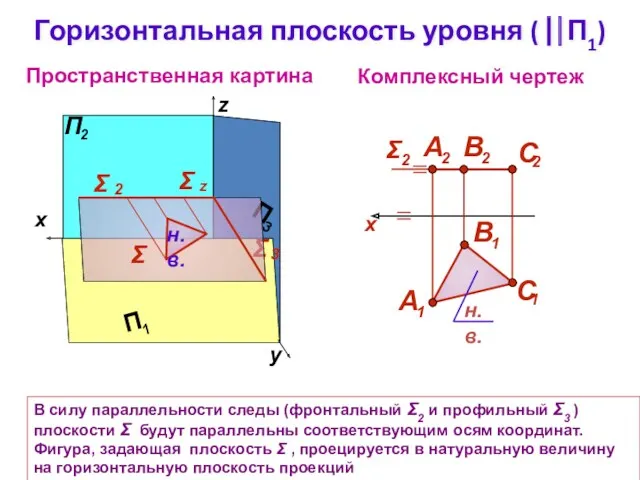
- 8. Горизонтальная плоскость уровня ( ⎢⎢П1) Комплексный чертеж z Σ Пространственная картина В силу параллельности следы (фронтальный
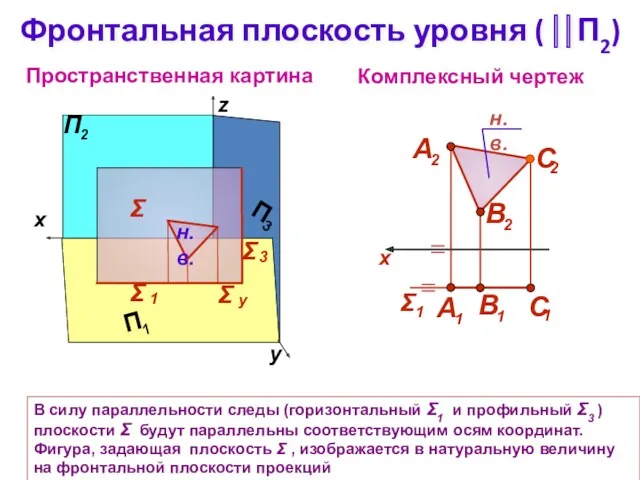
- 9. Фронтальная плоскость уровня ( ⎢⎢П2) Комплексный чертеж z Пространственная картина Σ В силу параллельности следы (горизонтальный
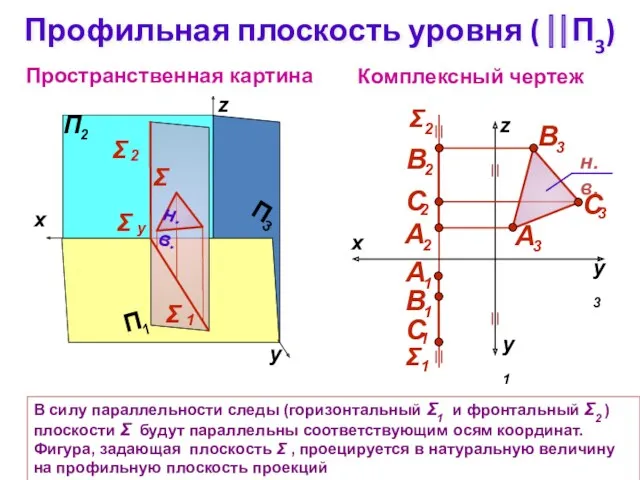
- 10. Профильная плоскость уровня ( ⎢⎢П3) Комплексный чертеж z Пространственная картина Σ В силу параллельности следы (горизонтальный
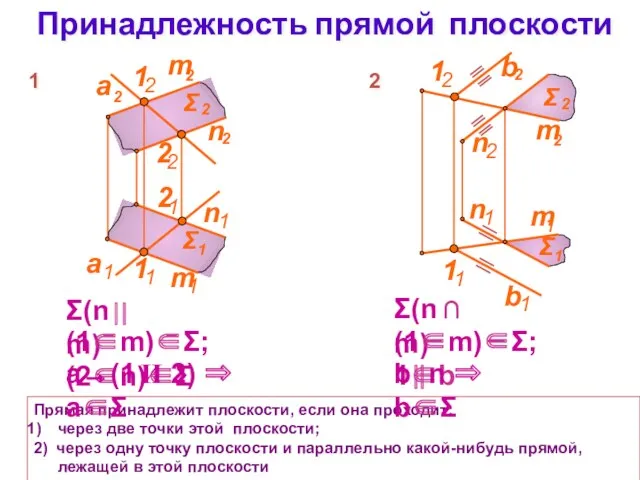
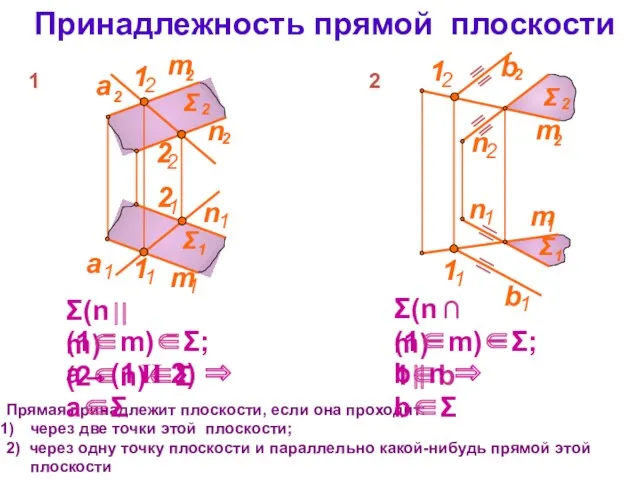
- 11. Принадлежность прямой плоскости Прямая принадлежит плоскости, если она проходит: через две точки этой плоскости; 2) через
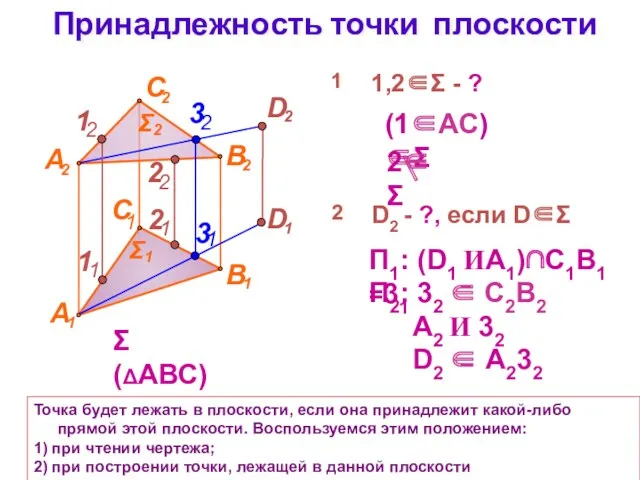
- 12. Принадлежность точки плоскости Точка будет лежать в плоскости, если она принадлежит какой-либо прямой этой плоскости. Воспользуемся
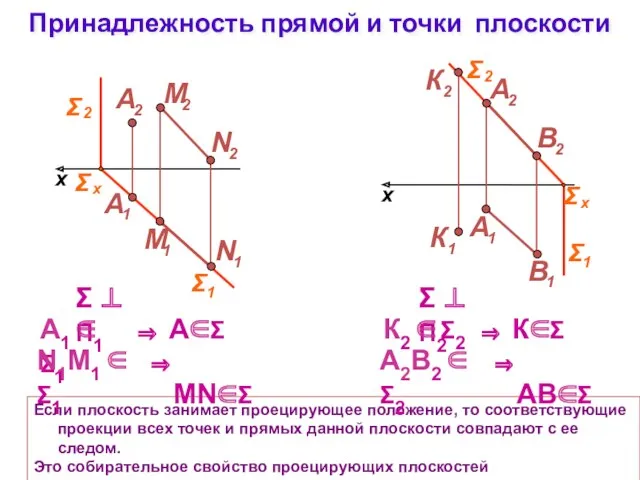
- 13. Принадлежность прямой и точки плоскости Если плоскость занимает проецирующее положение, то соответствующие проекции всех точек и
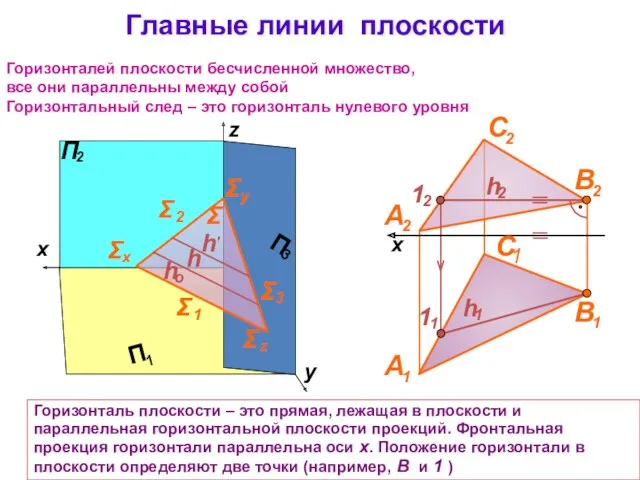
- 14. Главные линии плоскости Горизонталь плоскости – это прямая, лежащая в плоскости и параллельная горизонтальной плоскости проекций.
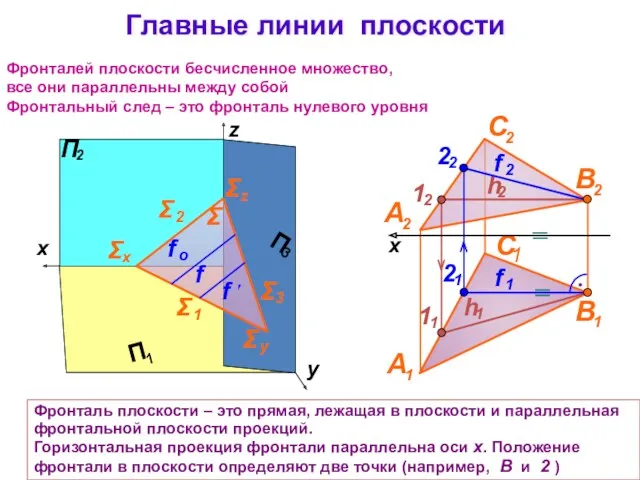
- 15. Главные линии плоскости Σ Фронталей плоскости бесчисленное множество, все они параллельны между собой Фронтальный след –
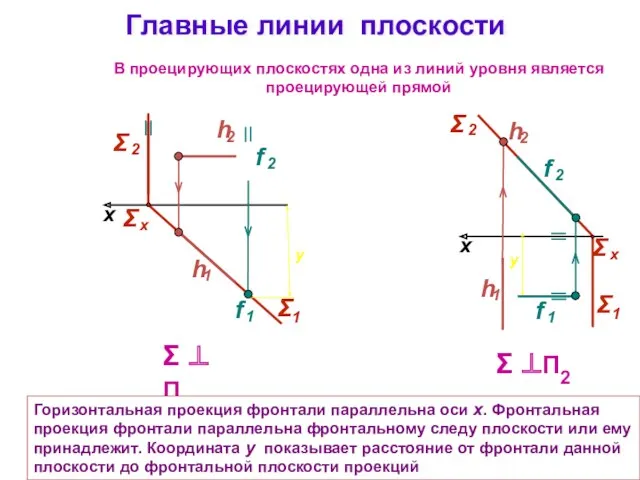
- 16. Главные линии плоскости Σ ⊥ П1 x Σ ⊥П2 x В проецирующих плоскостях одна из линий
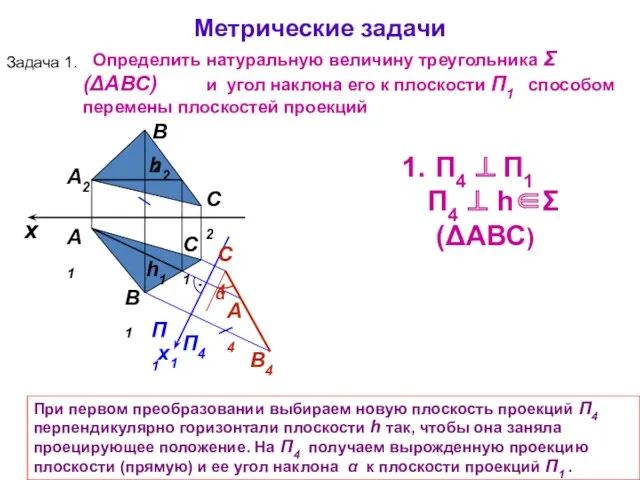
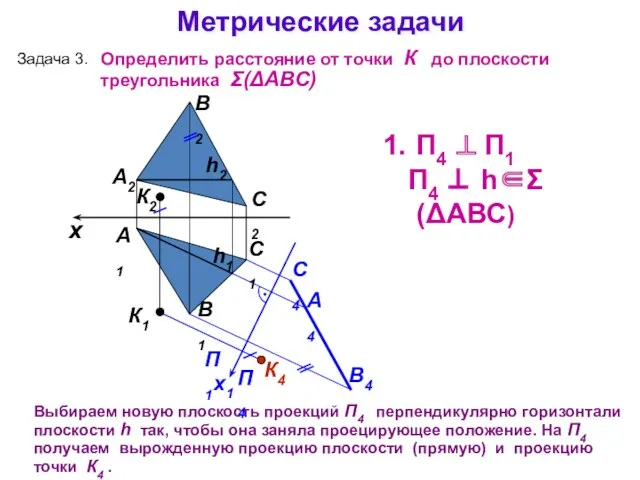
- 17. А1 А2 При первом преобразовании выбираем новую плоскость проекций П4 перпендикулярно горизонтали плоскости h так, чтобы
- 18. x А1 А2 П1 П4 x1 П4 ⊥ П1 П4 ⊥ h∈Σ(ΔАВС) 2. П5 ⊥ П4
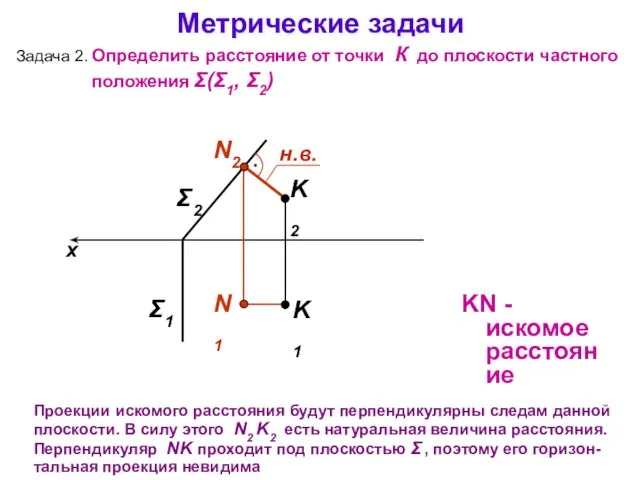
- 19. Метрические задачи Задача 2. Определить расстояние от точки К до плоскости частного положения Σ(Σ1, Σ2) x
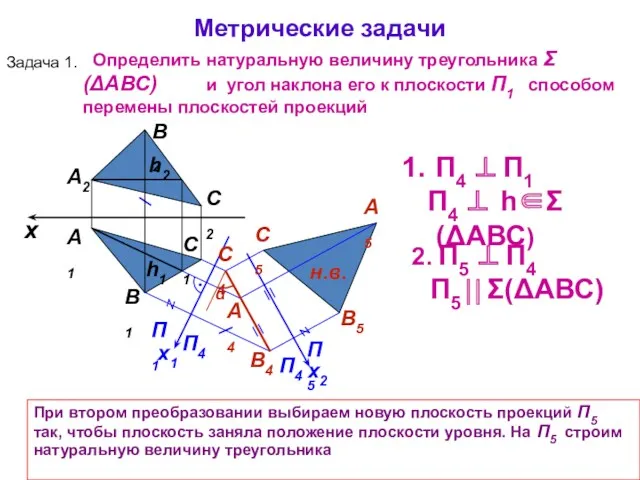
- 20. Метрические задачи А1 А2 Выбираем новую плоскость проекций П4 перпендикулярно горизонтали плоскости h так, чтобы она
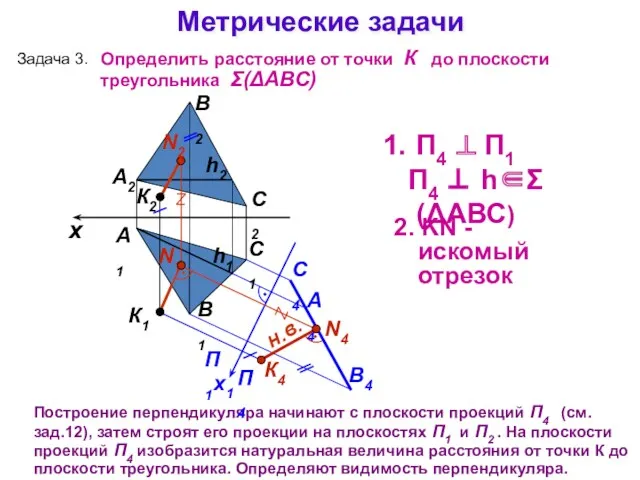
- 21. А1 А2 Построение перпендикуляра начинают с плоскости проекций П4 (см. зад.12), затем строят его проекции на
- 22. Взаимное положение прямой и плоскости, двух плоскостей. Позиционные задачи
- 23. Взаимное положение прямой и плоскости, двух плоскостей Прямая принадлежит плоскости (см. тема 3): все точки прямой
- 24. Принадлежность прямой плоскости Прямая принадлежит плоскости, если она проходит: через две точки этой плоскости; 2) через
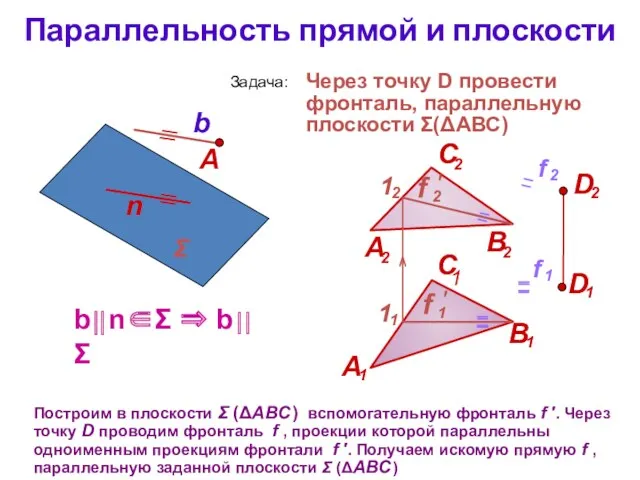
- 25. Параллельность прямой и плоскости Через точку А в пространстве можно провести бесчисленное множество прямых линий, параллельных
- 26. Параллельность прямой и плоскости Построим в плоскости Σ (ΔАВС ) вспомогательную фронталь f ′. Через точку
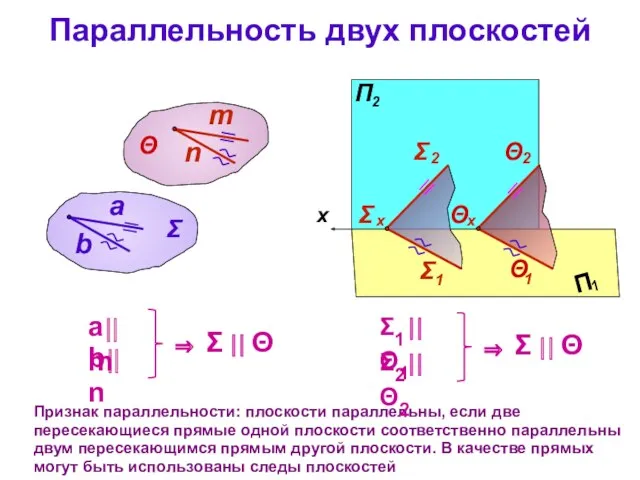
- 27. Параллельность двух плоскостей Признак параллельности: плоскости параллельны, если две пересекающиеся прямые одной плоскости соответственно параллельны двум
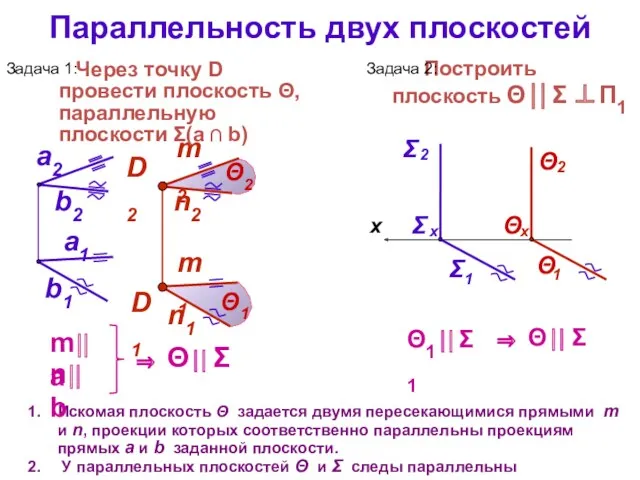
- 28. Параллельность двух плоскостей Искомая плоскость Θ задается двумя пересекающимися прямыми m и n, проекции которых соответственно
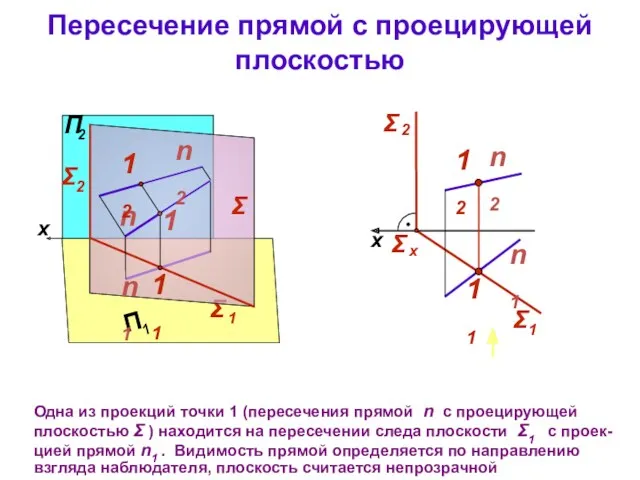
- 29. Σ Пересечение прямой с проецирующей плоскостью Одна из проекций точки 1 (пересечения прямой n с проецирующей
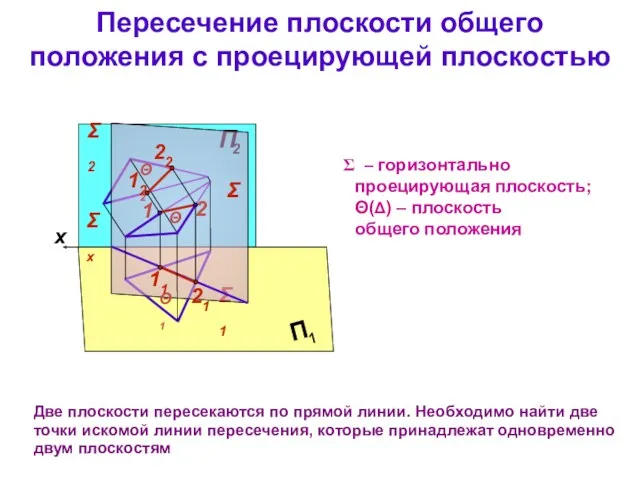
- 30. Пересечение плоскости общего положения с проецирующей плоскостью Две плоскости пересекаются по прямой линии. Необходимо найти две
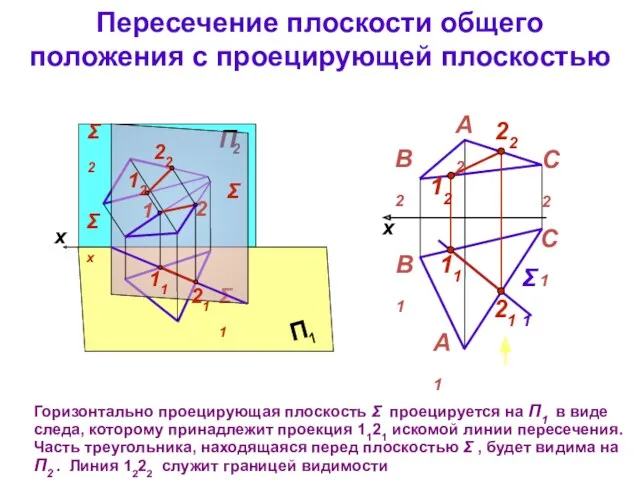
- 31. Пересечение плоскости общего положения с проецирующей плоскостью Горизонтально проецирующая плоскость Σ проецируется на П1 в виде
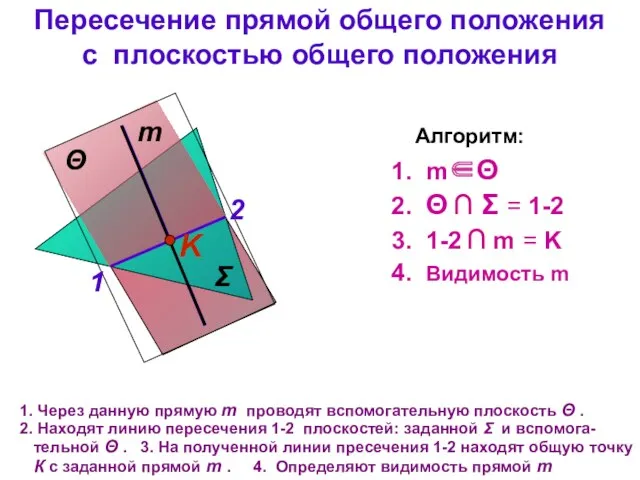
- 32. Пересечение прямой общего положения с плоскостью общего положения Σ m Через данную прямую m проводят вспомогательную
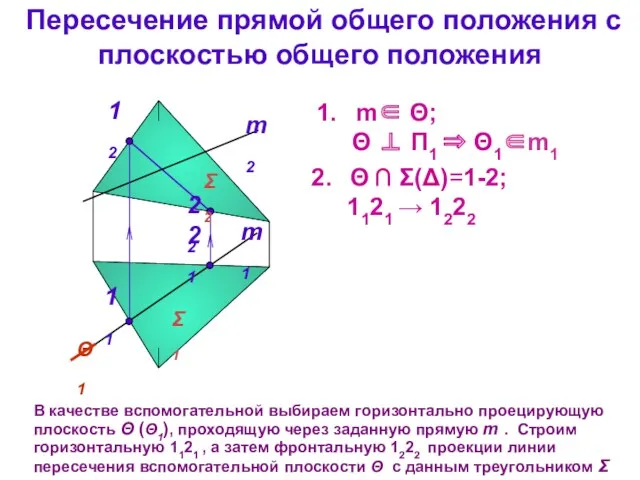
- 33. Пересечение прямой общего положения с плоскостью общего положения m1 m2 В качестве вспомогательной выбираем горизонтально проецирующую
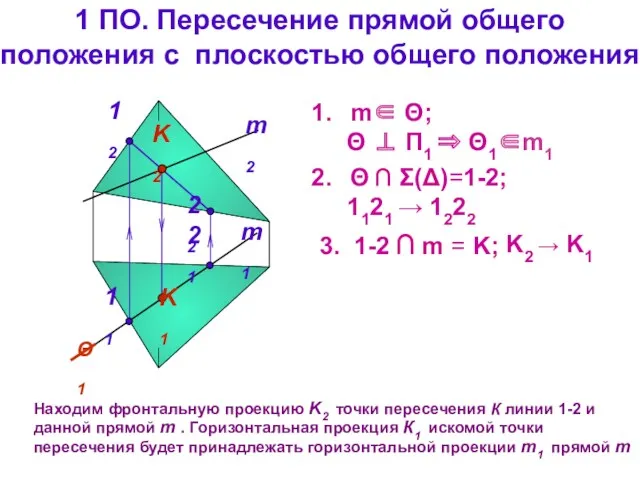
- 34. 1 ПО. Пересечение прямой общего положения с плоскостью общего положения m1 m2 Находим фронтальную проекцию K2
- 36. Скачать презентацию




 Деталирование сборочного чертежа. Порядок деталирования
Деталирование сборочного чертежа. Порядок деталирования Сечения. Алгоритм построения
Сечения. Алгоритм построения Графическая работа Соединение болтовое
Графическая работа Соединение болтовое Резьба. Классификация резьбы
Резьба. Классификация резьбы Зображення об’єктів на технічних креслениках. Види. Лекція 2
Зображення об’єктів на технічних креслениках. Види. Лекція 2 Изображение ландшафта средствами графики
Изображение ландшафта средствами графики Проецирование на три плоскости проекций. 8 класс
Проецирование на три плоскости проекций. 8 класс Стадии проектирования зданий. Маркировка строительных чертежей (лекция №2)
Стадии проектирования зданий. Маркировка строительных чертежей (лекция №2) Задание точки, прямой, плоскости и многогранников на комплексном эпюре (чертеже) Монжа
Задание точки, прямой, плоскости и многогранников на комплексном эпюре (чертеже) Монжа Рабочие чертежи
Рабочие чертежи Конструкторская и технологическая документация
Конструкторская и технологическая документация Задание на проектирование - многоэтажный комплекс
Задание на проектирование - многоэтажный комплекс Базовые ГОСТы
Базовые ГОСТы Позиционные задачи
Позиционные задачи Чтение и деталирование чертежа сборочной единицы
Чтение и деталирование чертежа сборочной единицы Метрические задачи
Метрические задачи Основы стандартизации. ЕСКД. Форматы. Масштабы. Виды изделий и документов. Построение видов изображений
Основы стандартизации. ЕСКД. Форматы. Масштабы. Виды изделий и документов. Построение видов изображений Введение. Предмет и метод начертательной геометрии (лекция № 1)
Введение. Предмет и метод начертательной геометрии (лекция № 1)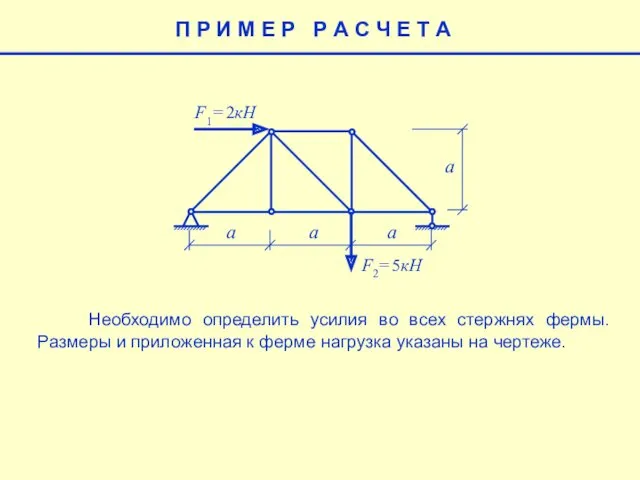 Определить усилия во всех стержнях фермы методом вырезания узлов
Определить усилия во всех стержнях фермы методом вырезания узлов Построение третьего вида по двум данным
Построение третьего вида по двум данным Поверхности. Лекция 7
Поверхности. Лекция 7 Общие правила выполнения чертежей. Форматы
Общие правила выполнения чертежей. Форматы Инженерная графика. Резьба
Инженерная графика. Резьба 20231103_23_urok_nanesenie_razmerov_s_uchetom_geometricheskoy_formy_predmeta
20231103_23_urok_nanesenie_razmerov_s_uchetom_geometricheskoy_formy_predmeta Основи машинобудівного креслення. Класифікація видів, розрізів, перетинів
Основи машинобудівного креслення. Класифікація видів, розрізів, перетинів Построения чертежей контуров технических деталей с использованием методов деления окружности на равные части
Построения чертежей контуров технических деталей с использованием методов деления окружности на равные части Виды проецирования
Виды проецирования Перспектива та її особливості
Перспектива та її особливості