Содержание
- 2. Appendix A: Details on estimation of factor modelsAppendix B: Details on Monte Carlo comparison Why factor
- 3. Appendix A: Details on estimation of factor modelsAppendix B: Details on Monte Carlo comparison Why factor
- 4. Appendix A: Details on estimation of factor modelsAppendix B: Details on Monte Carlo comparison What can
- 5. Appendix A: Details on estimation of factor modelsAppendix B: Details on Monte Carlo comparison An introduction
- 6. Appendix A: Details on estimation of factor modelsAppendix B: Details on Monte Carlo comparison Some extensions
- 7. Appendix A: Details on estimation of factor modelsAppendix B: Details on Monte Carlo comparison Representation Let
- 8. Appendix A: Details on estimation of factor modelsAppendix B: Details on Monte Carlo comparison Representation For
- 9. Appendix A: Details on estimation of factor modelsAppendix B: Details on Monte Carlo comparison Let us
- 10. Appendix A: Details on estimation of factor modelsAppendix B: Details on Monte Carlo comparison In the
- 11. Appendix A: Details on estimation of factor modelsAppendix B: Details on Monte Carlo comparison Additional lags
- 12. Appendix A: Details on estimation of factor modelsAppendix B: Details on Monte Carlo comparison Let us
- 13. Appendix A: Details on estimation of factor modelsAppendix B: Details on Monte Carlo comparison Identification Let
- 14. Appendix A: Details on estimation of factor modelsAppendix B: Details on Monte Carlo comparison Typical restrictions
- 15. Appendix A: Details on estimation of factor modelsAppendix B: Details on Monte Carlo comparison The condition
- 16. Appendix A: Details on estimation of factor modelsAppendix B: Details on Monte Carlo comparison Factor models
- 17. Appendix A: Details on estimation of factor modelsAppendix B: Details on Monte Carlo comparison Let us
- 18. Appendix A: Details on estimation of factor modelsAppendix B: Details on Monte Carlo comparison Estimation by
- 19. Appendix A: Details on estimation of factor modelsAppendix B: Details on Monte Carlo comparison Hence, the
- 20. Appendix A: Details on estimation of factor modelsAppendix B: Details on Monte Carlo comparison However, there
- 21. Appendix A: Details on estimation of factor modelsAppendix B: Details on Monte Carlo comparison Non-parametric, large
- 22. Appendix A: Details on estimation of factor modelsAppendix B: Details on Monte Carlo comparison The SW
- 23. Appendix A: Details on estimation of factor modelsAppendix B: Details on Monte Carlo comparison The SW
- 24. Appendix A: Details on estimation of factor modelsAppendix B: Details on Monte Carlo comparison The SW
- 25. Appendix A: Details on estimation of factor modelsAppendix B: Details on Monte Carlo comparison The SW
- 26. Appendix A: Details on estimation of factor modelsAppendix B: Details on Monte Carlo comparison The SW
- 27. Appendix A: Details on estimation of factor modelsAppendix B: Details on Monte Carlo comparison The SW
- 28. Appendix A: Details on estimation of factor modelsAppendix B: Details on Monte Carlo comparison The FHLR
- 29. Appendix A: Details on estimation of factor modelsAppendix B: Details on Monte Carlo comparison The FHLR
- 30. Appendix A: Details on estimation of factor modelsAppendix B: Details on Monte Carlo comparison The FHLR
- 31. Appendix A: Details on estimation of factor modelsAppendix B: Details on Monte Carlo comparison The FHLR
- 32. Appendix A: Details on estimation of factor modelsAppendix B: Details on Monte Carlo comparison Parametric estimation
- 33. Appendix A: Details on estimation of factor modelsAppendix B: Details on Monte Carlo comparison Parametric estimation
- 34. Appendix A: Details on estimation of factor modelsAppendix B: Details on Monte Carlo comparison Parametric estimation
- 35. Appendix A: Details on estimation of factor modelsAppendix B: Details on Monte Carlo comparison Parametric estimation
- 36. Appendix A: Details on estimation of factor modelsAppendix B: Details on Monte Carlo comparison Parametric estimation
- 37. Appendix A: Details on estimation of factor modelsAppendix B: Details on Monte Carlo comparison Factor estimation
- 38. Appendix A: Details on estimation of factor modelsAppendix B: Details on Monte Carlo comparison Factor estimation
- 39. Appendix A: Details on estimation of factor modelsAppendix B: Details on Monte Carlo comparison Factor models
- 40. Appendix A: Details on estimation of factor modelsAppendix B: Details on Monte Carlo comparison Factor models
- 41. Appendix A: Details on estimation of factor modelsAppendix B: Details on Monte Carlo comparison Structural Factor
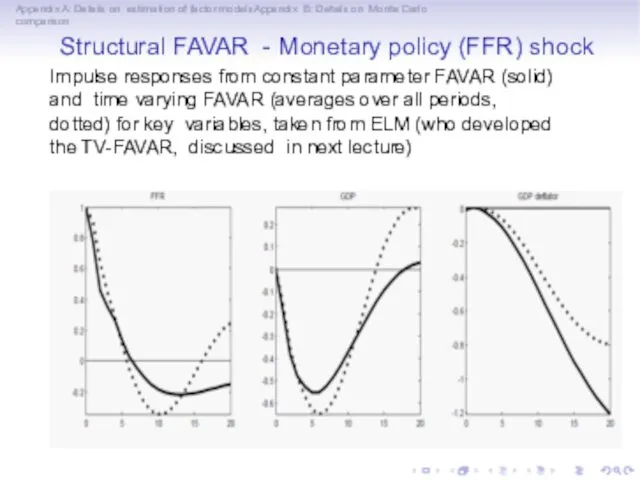
- 42. Appendix A: Details on estimation of factor modelsAppendix B: Details on Monte Carlo comparison Structural FAVAR
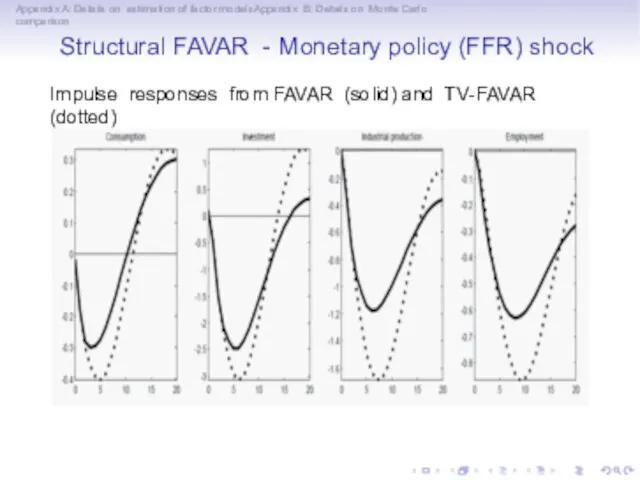
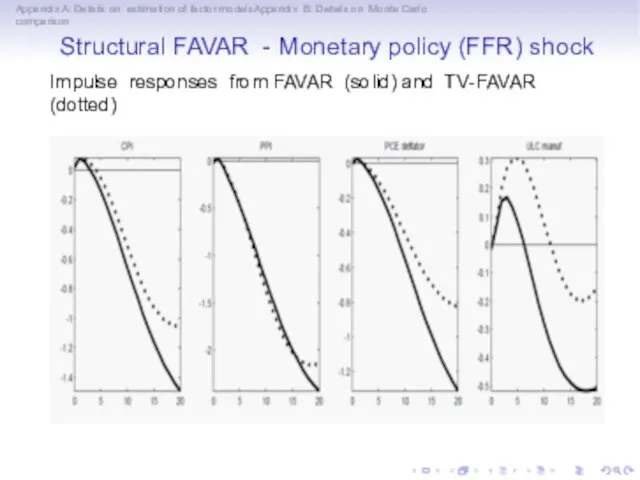
- 43. Appendix A: Details on estimation of factor modelsAppendix B: Details on Monte Carlo comparison Structural FAVAR
- 44. Appendix A: Details on estimation of factor modelsAppendix B: Details on Monte Carlo comparison Structural FAVAR
- 45. Appendix A: Details on estimation of factor modelsAppendix B: Details on Monte Carlo comparison Structural FAVAR
- 46. Appendix A: Details on estimation of factor modelsAppendix B: Details on Monte Carlo comparison Structural FAVAR
- 47. Appendix A: Details on estimation of factor modelsAppendix B: Details on Monte Carlo comparison Structural FAVAR
- 48. Appendix A: Details on estimation of factor modelsAppendix B: Details on Monte Carlo comparison Structural FAVAR
- 49. Appendix A: Details on estimation of factor modelsAppendix B: Details on Monte Carlo comparison Structural FAVAR:
- 50. Appendix A: Details on estimation of factor modelsAppendix B: Details on Monte Carlo comparison References Amengual,
- 51. Appendix A: Details on estimation of factor modelsAppendix B: Details on Monte Carlo comparison Banerjee, A.,
- 52. Appendix A: Details on estimation of factor modelsAppendix B: Details on Monte Carlo comparison Doz, C.,
- 53. Appendix A: Details on estimation of factor modelsAppendix B: Details on Monte Carlo comparison Forni, M.,
- 54. Appendix A: Details on estimation of factor modelsAppendix B: Details on Monte Carlo comparison Lutkepohl, H.
- 55. Appendix A: Details on estimation of factor modelsAppendix B: Details on Monte Carlo comparison Stock, J.H
- 56. Appendix A: Details on estimation of factor modelsAppendix B: Details on Monte Carlo comparison Stock, J.H.
- 57. Appendix A: Details on estimation of factor modelsAppendix B: Details on Monte Carlo comparison The FHLR
- 58. Appendix A: Details on estimation of factor modelsAppendix B: Details on Monte Carlo comparison The FHLR
- 59. Appendix A: Details on estimation of factor modelsAppendix B: Details on Monte Carlo comparison Parametric estimation
- 60. Appendix A: Details on estimation of factor modelsAppendix B: Details on Monte Carlo comparison Parametric estimation
- 61. Appendix A: Details on estimation of factor modelsAppendix B: Details on Monte Carlo comparison Parametric estimation
- 62. Appendix A: Details on estimation of factor modelsAppendix B: Details on Monte Carlo comparison Factor estimation
- 63. Appendix A: Details on estimation of factor modelsAppendix B: Details on Monte Carlo comparison Factor estimation
- 64. Appendix A: Details on estimation of factor modelsAppendix B: Details on Monte Carlo comparison Factor estimation
- 65. Appendix A: Details on estimation of factor modelsAppendix B: Details on Monte Carlo comparison Factor estimation
- 66. Appendix A: Details on estimation of factor modelsAppendix B: Details on Monte Carlo comparison Factor estimation
- 68. Скачать презентацию






























































 Администрация Сергиево-посадского муниципального района
Администрация Сергиево-посадского муниципального района Экономика Японии
Экономика Японии Мировой Экономический Кризис
Мировой Экономический Кризис Валовой внутренний продукт (ВВП) и другие показатели, рассчитываемые на основе ВВП
Валовой внутренний продукт (ВВП) и другие показатели, рассчитываемые на основе ВВП Анализ и совершенствование системы контроля качества продукции на предприятии (на примере ООО Волгопромстрой)
Анализ и совершенствование системы контроля качества продукции на предприятии (на примере ООО Волгопромстрой) Территория опережающего социально-экономического развития
Территория опережающего социально-экономического развития Микроэкономика и макроэкономика
Микроэкономика и макроэкономика Volkswagen company
Volkswagen company Статистика окружающей среды и природных ресурсов
Статистика окружающей среды и природных ресурсов Центральные банки. Сущность, функции и роль в регулировании экономики
Центральные банки. Сущность, функции и роль в регулировании экономики Studiu Individual la disciplina ,,Economia Turismului”
Studiu Individual la disciplina ,,Economia Turismului” Трудовые ресурсы
Трудовые ресурсы Основи економічної теорії. Тема 5. Підприємство (фірма)
Основи економічної теорії. Тема 5. Підприємство (фірма) Эффективность исполнения переданных полномочий в области лесных отношений субъектами Российской Федерации
Эффективность исполнения переданных полномочий в области лесных отношений субъектами Российской Федерации G-global project and energy-saving strategies
G-global project and energy-saving strategies Квалиметрия, как наука. (Тема 2)
Квалиметрия, как наука. (Тема 2) Важные аспекты работы центра занятости населения
Важные аспекты работы центра занятости населения Теория потребительского поведения
Теория потребительского поведения Расходы и прибыль фирмы
Расходы и прибыль фирмы Социально-экономические показатели стран и регионов
Социально-экономические показатели стран и регионов Экономика города Омска и Омской области
Экономика города Омска и Омской области Podniková ekonomika (POEKR, PODEK)
Podniková ekonomika (POEKR, PODEK) Экономиканы мемлекеттік реттеудің субъектілері мен объектілері
Экономиканы мемлекеттік реттеудің субъектілері мен объектілері Халықаралық экономикалық интеграция
Халықаралық экономикалық интеграция Международная сегментация и стратегии проникновения на зарубежные рынки
Международная сегментация и стратегии проникновения на зарубежные рынки Финансовые модели и оценка бизнеса
Финансовые модели и оценка бизнеса Деньги и их роль в регулировании экономики
Деньги и их роль в регулировании экономики Pozyskiwanie funduszy unijnych - dofinansowanie projektu
Pozyskiwanie funduszy unijnych - dofinansowanie projektu