Содержание
- 2. Introduction and Motivation The dynamics of a time series can be influenced by “unobservable” (sometimes called
- 3. Introduction and Motivation (continued) State space representation is a way to describe the law of motion
- 4. Common Usage of These Techniques Macroeconomics, finance, time series models Autopilot, radar tracking Orbit tracking, satellite
- 5. Another example Use nightlight data and the Kalman filter to adjust official GDP growth statistics. The
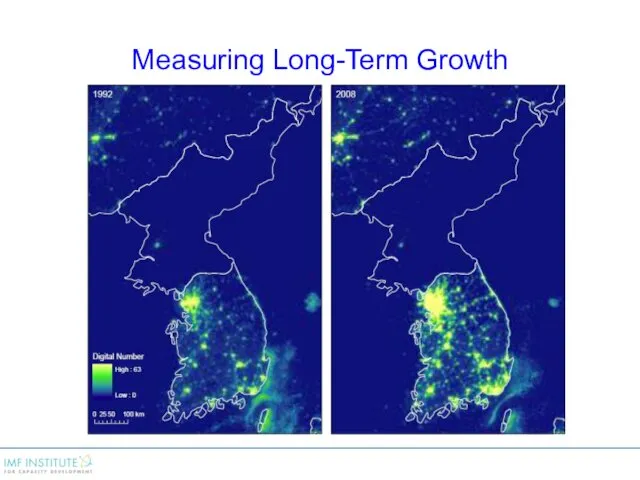
- 6. Measuring Long-Term Growth
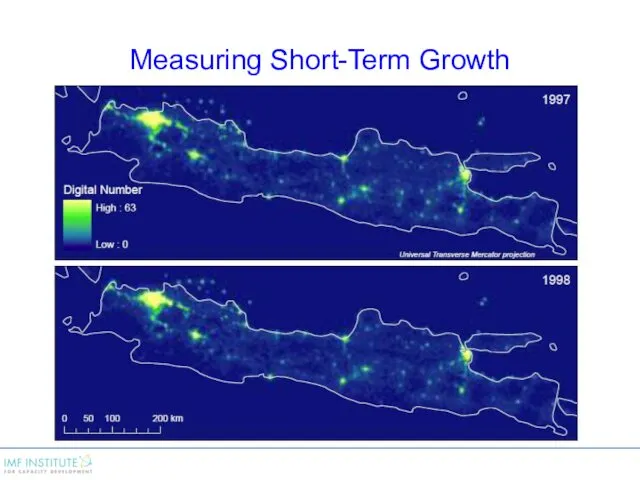
- 7. Measuring Short-Term Growth
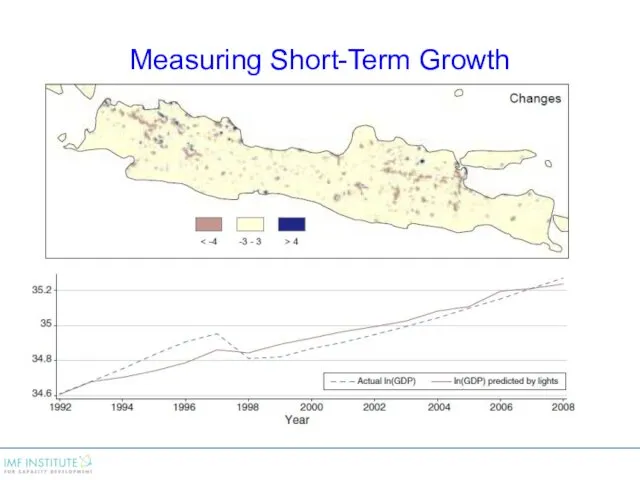
- 8. Measuring Short-Term Growth
- 9. Content Outline: Lecture Segments State Space Representation The Kalman Filter Maximum Likelihood Estimation and Kalman Smoothing
- 10. Content Outline: Workshops Workshops Estimation of equilibrium real interest rate, trend growth rate, and potential output
- 11. State Space Representation
- 12. Basic Setup Let yt be an (or a vector) observable variable(s) at time t. E.g., return
- 13. Basic Setup The state-space representation of the dynamics of yt is given by : We assume
- 14. Basic Setup The state-space representation of the dynamics of yt is given by : with The
- 15. Basic Setup The error terms in the two equations are such that: State equation Observation equation
- 16. What if you know that are serially correlated: and , Then so one of the assumptions
- 17. The State Space Representation: Examples Example #1: simple version of the CAPM st one variable, return
- 18. Example #2: growth and real business cycle (small open economy with a large export sector) st
- 19. Example #3: interest rates on zero-coupon bonds of different maturity st one variable, latent variable yt
- 20. Example #4: an AR(2) process Can we still apply the state space representation? Yes! Consider the
- 21. Example #4: an AR(2) process The state equation: And the observation equation: What are matrices Ω
- 22. Consider the same AR(2) process Another possible state equation: And the corresponding observation equation: These two
- 23. Example #5: an MA(2) process Consider the following state equation: And the observation equation: What are
- 24. Example #5: an MA(2) process Consider the following state equation: And the observation equation: What are
- 25. Example #6: A random walk plus drift process State equation? Observation equation? What are the loadings
- 26. In this course we will deal only with stable systems: Such systems that for any initial
- 27. The Kalman Filter
- 28. State Space Representation [univariate case]: Notation: is the best linear predictor of st conditional on the
- 29. Kalman Filter: Main Idea Moving from t-1 to t Suppose we know and at time t-1.
- 30. Kalman Filter: Main Idea How to update st|t ? Idea: use the observed prediction error to
- 31. Kalman Filter: More Notations is the prediction error variance of given the history of observed variables
- 32. Kalman Gain: Intuition Kalman gain is chosen so that is minimized. It can be shown that
- 33. Kalman Filter: Example Kalman gain is Consider State equation Observation equation Additionally , where is a
- 34. Kalman Filter: The last step How do we get from to using ? Recall that for
- 35. Kalman Filter: Finally From the previous slide st|t = st|t-1+βPt|t-1(Ft|t-1)-1(yt - yt|t-1) Pt|t = Pt|t-1 –
- 36. Kalman Filter: Review We start from and . yt|t-1 = αxt + βst|t-1 Calculate Kalman gain
- 37. Kalman Filter: How to choose initial state If the sample size is large, the choice of
- 38. Kalman Filter as a Recursive Regression Consider a regular regression function where Substituting From one of
- 39. Kalman Filter as a Recursive Regression Consider a regular regression function where Substituting From one of
- 40. Kalman Filter as a Recursive Regression Thus the Kalman filter can be interpreted as a recursive
- 41. Optimality of the Kalman Filter Using the property of OLS estimates that constructed residuals are uncorrelated
- 42. Kalman Filter Some comments Within the class of linear (in observables) predictors the Kalman filter algorithm
- 43. Kalman Filter - Multivariate Case The Kalman Filter algorithm can be easily generalized to the generic
- 44. Kalman Filter Algorithm – Multivariate Case
- 45. Kalman Filter Algorithm – Multivariate Case (cont.)
- 46. Kalman Filter Algorithm – Multivariate Case (cont.)
- 47. ML Estimation and Kalman Smoothing
- 48. Maximum Likelihood Estimation The algorithm in the previous section assumes knowledge of the parameters. If these
- 49. To estimate model parameters through maximizing log-likelihood: Step 1: For every set of the underlying parameters,
- 50. Kalman Smoothing For each period t, the Kalman filter uses only information available up to time
- 51. Kalman Smoothing Using the same principles for normal conditional distribution, it is possible to show that
- 53. Скачать презентацию























![State Space Representation [univariate case]: Notation: is the best linear](/_ipx/f_webp&q_80&fit_contain&s_1440x1080/imagesDir/jpg/96593/slide-27.jpg)























 Равнодействующая сил
Равнодействующая сил Protein structure: prediction engineering design
Protein structure: prediction engineering design Механика жидкостей и газов. (Лекция 9)
Механика жидкостей и газов. (Лекция 9) Масса тела
Масса тела Ремонт автомобилей. Ремонт коленчатых валов и шатунов. (Тема 4.5)
Ремонт автомобилей. Ремонт коленчатых валов и шатунов. (Тема 4.5) Техническое обслуживание рулевого управления автомобиля Toyota Mark II
Техническое обслуживание рулевого управления автомобиля Toyota Mark II Простые механизмы в технике и в быту
Простые механизмы в технике и в быту Машиноведение. История создания швейной машины
Машиноведение. История создания швейной машины Тепловое излучение. Задачи
Тепловое излучение. Задачи Что изучает физика? Некоторые физические термины
Что изучает физика? Некоторые физические термины Прості механізми побутових пристроїв
Прості механізми побутових пристроїв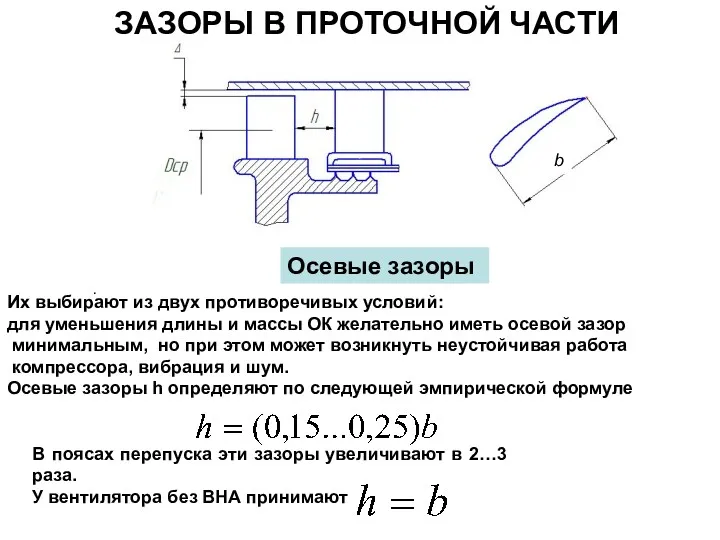 Зазоры в проточной части
Зазоры в проточной части Магнитное поле. Взаимодействие токов
Магнитное поле. Взаимодействие токов Механізація подрібнення стеблових кормів
Механізація подрібнення стеблових кормів Сила трения. Трение в природе и технике
Сила трения. Трение в природе и технике Ремонт авиационного оборудования с боевыми и эксплуатационными повреждениями
Ремонт авиационного оборудования с боевыми и эксплуатационными повреждениями Коробки перемены передач
Коробки перемены передач Электромагнитное поле
Электромагнитное поле Физика в нашей жизни
Физика в нашей жизни Влияние на работу дороги природных факторов
Влияние на работу дороги природных факторов Внутрішня енергія
Внутрішня енергія Основы поверхностной обработки полупроводниковых материалов
Основы поверхностной обработки полупроводниковых материалов Урок презентация Реактивное движение
Урок презентация Реактивное движение Закон Ома на участке цепи. Диаграмма связи величин: U, I, R
Закон Ома на участке цепи. Диаграмма связи величин: U, I, R Разработка установки для замены масла в двигателе
Разработка установки для замены масла в двигателе Закон всемирного тяготения
Закон всемирного тяготения Магнитное поле
Магнитное поле Ионизирующие излучения
Ионизирующие излучения