Содержание
- 2. Заряди і поля У Всесвіті на всіх масштабах від елементарних частинок до Метагалактики взаємодія між структурними
- 3. Силове поле Силове поле – це простір, в кожній точці якого на вміщену туди частинку (пробне
- 4. Силове поле Потенціальна енергія – можливість виконувати роботу при переміщенні частинки з однієї точки поля консерва-тивних
- 5. Силове поле Робота з переміщення заряду q в полі заряду Q по траєкторії 1-a-b-2 дорівнює роботі
- 6. Силове поле Потенціал – це потенціальна енергія одиничного пробного тіла. Тоді різниця потенціалів – це робота
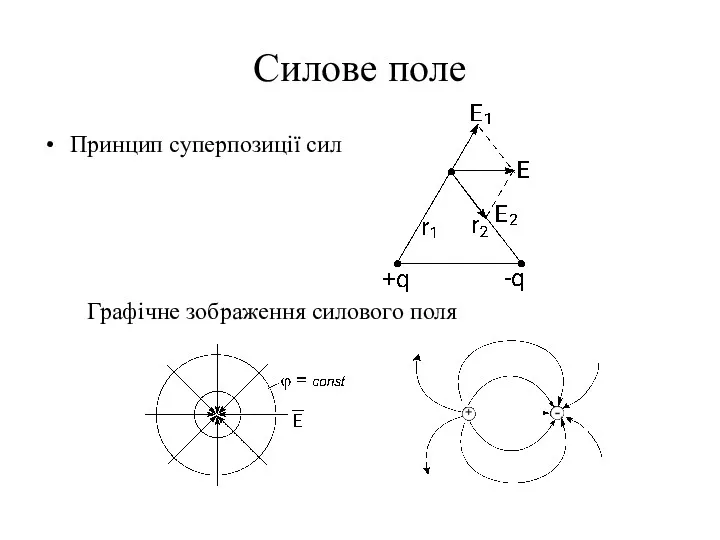
- 7. Силове поле Принцип суперпозиції сил Графічне зображення силового поля
- 8. Властивості векторних полів. Дивергенція. Теорема Остроградського-Гауса. Потік вектора через деяку поверхню і циркуляція вектора по заданому
- 9. Дивергенція Отже, за визначенням Аналогічно для довільного вектора Ця величина не може залежати від форми поверхні,
- 10. Дивергенція Розглянемо в точці P(x,y,z) малий об'єм у формі паралелепіпеда dxdydz. Потік через цю поверхню складається
- 11. Дивергенція. Теорема Остроградського-Гауса Аналогічно отримаємо Отже, потік Нарешті Знаючи , можна знайти потік через довільну повер-хню:
- 12. Михайло Васильович Остроградський (24.09.1801, Полтавська губ. – 01.01.1862) Український математик і механік, лідер математиків Російської імперії.
- 13. Карл Фрі́дріх Га́ус (Johann Carl Friedrich Gauß, 30.04.1777 – 23.02.1855) Видатний німецький математик, астроном і фізик.
- 14. Циркуляція. Ротор. Теорема Стокса. Тепер розглянемо циркуляцію по контуру. Γ Якщо це рух рідини, то циркуляція
- 15. Джордж Габріе́ль Стокс (George Gabriel Stokes; 13.08.1819 – 01.02.1903) Англійський математик і фізик ірландського походження. Навчався
- 16. Циркуляція. Як характеристику поля в т. Р беруть В залежності від напрямку обходу точки Р величина
- 17. Ротор Знайдемо вираз для y z 1 2 3 4 Визначимо проекцію для площадки dydz, n||x.
- 18. Ротор Отже Аналогічно Ці вирази можна отримати один з одного шляхом циклічної перестановки індексів (z →x
- 19. Теорема Стокса Разом: Знаючи ротор в кожній точці поверхні S, можна знайти циркуляцію вектора по контуру,
- 20. Диференціальний оператор Записи векторного аналізу спрощуються, якщо ввести диференціальний оператор Тоді, діючи вектором на скаляр, отримаємо
- 21. Диференціальний оператор Векторний добуток Оператор діє на функцію, яка стоїть справа від нього.
- 22. Диференціальний оператор паралельні вектори, тому векторний добуток дорівнює нулю. Електростатичне поле E = -∇φ, rotE =
- 23. Циркуляція вектора напруженості. Потік вектора напруженості. Рівняння Пуасона. В потенціальному полі Тут dℓ направлене по дотичній
- 24. Потік вектора напруженості Потік вектора Е: Візьмемо замкнуту поверхню у вигляді сфери. Тоді Якщо зарядів багато
- 25. Потік вектора напруженості Введемо вектор електричної індукції В такому разі Для гравітаційного поля Згідно з теоремою
- 26. Потік вектора напруженості Густина заряду В такому разі Аналогічно
- 27. Потік вектора напруженості Поле рівномірно зарядженої сфери. Всередині сфери (r оскільки там зарядів немає. Поза сферою:
- 28. Рівняння Пуасона Рівняння дозволяє знайти потенціал, коли відомий розподіл заряду в просторі.
- 30. Скачать презентацию


























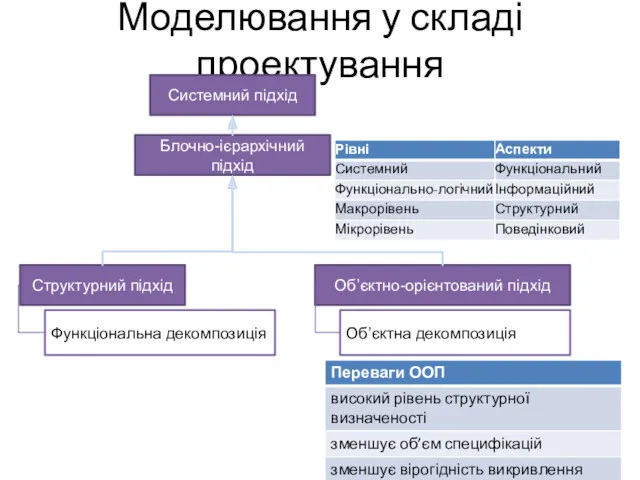 Моделювання у складі проектування
Моделювання у складі проектування Взаємодія тіл і сила
Взаємодія тіл і сила Закон электромагнитной индукции
Закон электромагнитной индукции Термодинамические основы работы тепловых машин (теплотехника)
Термодинамические основы работы тепловых машин (теплотехника) Физические явления – основа разделения смесей в химии
Физические явления – основа разделения смесей в химии Теория радиосистем передачи информации. (Лекция 2)
Теория радиосистем передачи информации. (Лекция 2) Радиоактивность. Альфа-, гамма- и бета- излучения
Радиоактивность. Альфа-, гамма- и бета- излучения Сила тока. Условия, необходимые для существования электрического тока. Закон Ома для участка цепи. Сопротивление
Сила тока. Условия, необходимые для существования электрического тока. Закон Ома для участка цепи. Сопротивление Определение направления индукционного тока
Определение направления индукционного тока Физика и метод научного познания
Физика и метод научного познания Ядерная модель атома. Квантовые постулаты Бора
Ядерная модель атома. Квантовые постулаты Бора Физический бой для 7-9 классов
Физический бой для 7-9 классов Испарение и конденсация. Плавление и отвердевание
Испарение и конденсация. Плавление и отвердевание Работа и мощность электрического тока. 8 класс
Работа и мощность электрического тока. 8 класс Проек по теме Молния
Проек по теме Молния Электризация тел при соприкосновении. Взаимодействие заряженных частиц
Электризация тел при соприкосновении. Взаимодействие заряженных частиц лабораторная работа измерение плотности твердого тела
лабораторная работа измерение плотности твердого тела Основные положения общей теории относительности
Основные положения общей теории относительности Методи розрахунку електричних кіл постійного струму
Методи розрахунку електричних кіл постійного струму Изгиб. Основные понятия и допущения
Изгиб. Основные понятия и допущения Равномерное движение по окружности. Решение задач.
Равномерное движение по окружности. Решение задач.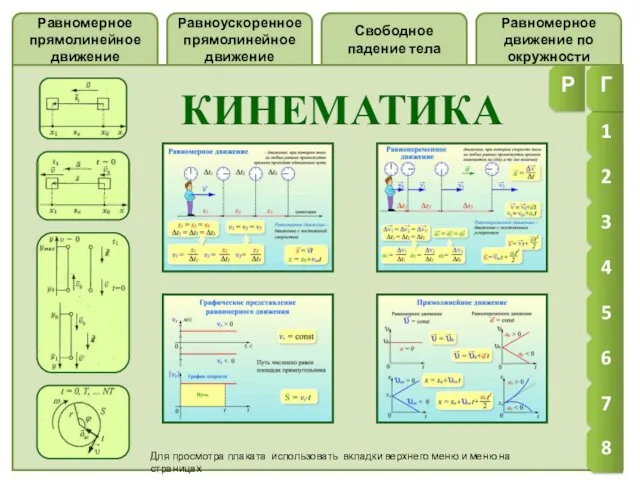 Кинематика
Кинематика Второй закон термодинамики
Второй закон термодинамики Заклепочное соединение
Заклепочное соединение Система EDS (Elektronische Differentialsperre) для автомобилей
Система EDS (Elektronische Differentialsperre) для автомобилей Цепная реакция деления ядер. Ядерный реактор
Цепная реакция деления ядер. Ядерный реактор дополнение к уроку физики Испарение- вопросы почемучки
дополнение к уроку физики Испарение- вопросы почемучки Условия плавания тел в жидкости. Лабораторная работа
Условия плавания тел в жидкости. Лабораторная работа