Содержание
- 2. Механические колебания
- 3. Лекция № 5 1. Равновесия устойчивое, неустойчивое, безразличное. 2. Модель гармонического осциллятора. 3. Свободные незатухающие колебания.
- 4. Колебаниями называются движения или процессы, которые характеризуются определенной повторяемостью во времени. Колебательные процессы широко распространены в
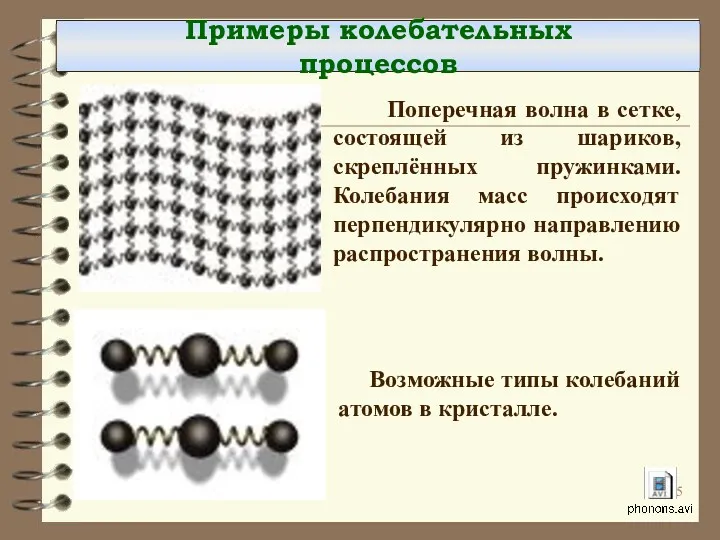
- 5. Возможные типы колебаний атомов в кристалле. Поперечная волна в сетке, состоящей из шариков, скреплённых пружинками. Колебания
- 6. Примеры колебательных процессов Круговая волна на поверхности жидкости, возбуждаемая точечным источником (гармонически колеблющимся шариком). Генерация акустической
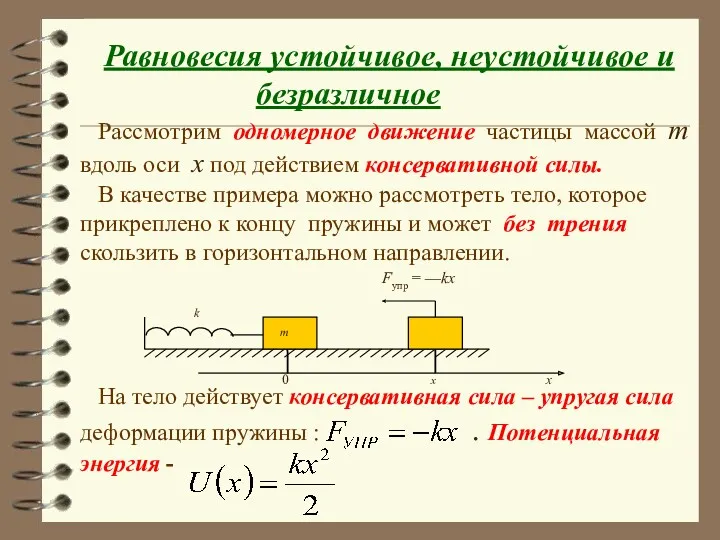
- 7. Равновесия устойчивое, неустойчивое и безразличное Рассмотрим одномерное движение частицы массой m вдоль оси x под действием
- 8. График потенциальной энергии имеет вид: Нас интересуют положения равновесия, равновесия, в кото в которых сила, действующая
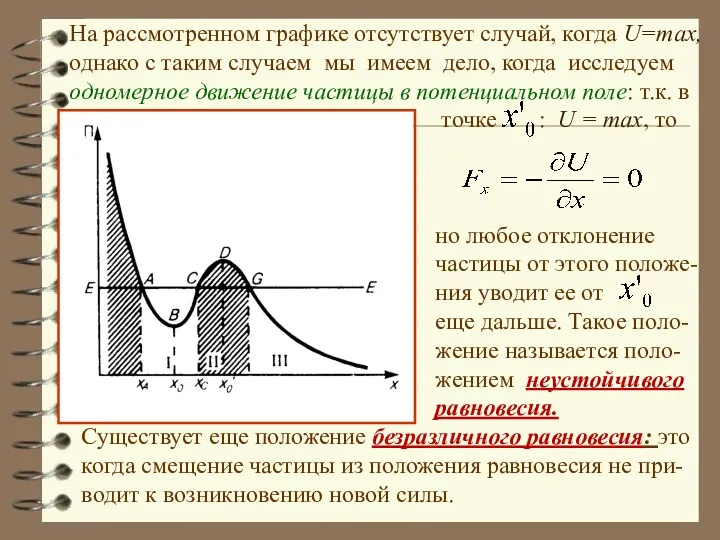
- 9. На рассмотренном графике отсутствует случай, когда U=max, однако с таким случаем мы имеем дело, когда исследуем
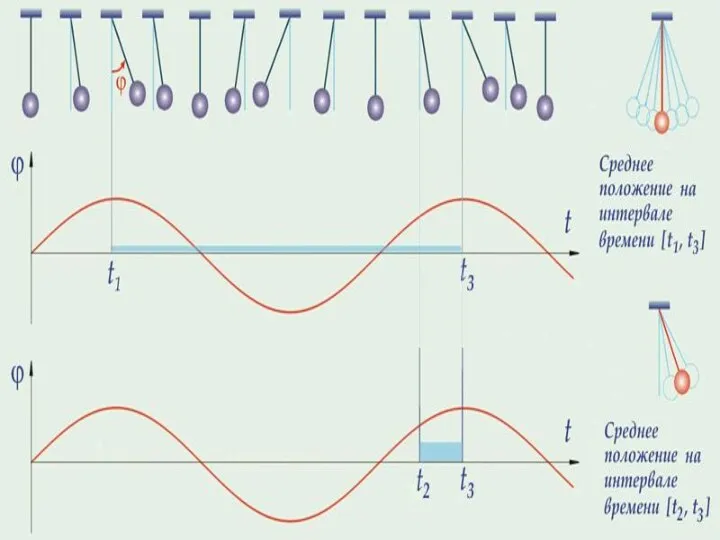
- 10. Колебания могут происходить только около положения устойчивого равновесия, где , а . Проанализируем процесс колебаний с
- 11. В результате потенциальная энергия принимает вид: , где . Найдем силу, действующую на частицу: Это выражение
- 12. Модель гармонического осциллятора Колебания называются свободными (или собственными), если они совершаются за счет первоначально сообщенной энергии
- 13. Тогда зависимость координаты от времени описываются уравнением следующего вида: где - амплитудой колебания, максимальное значение колеблющейся
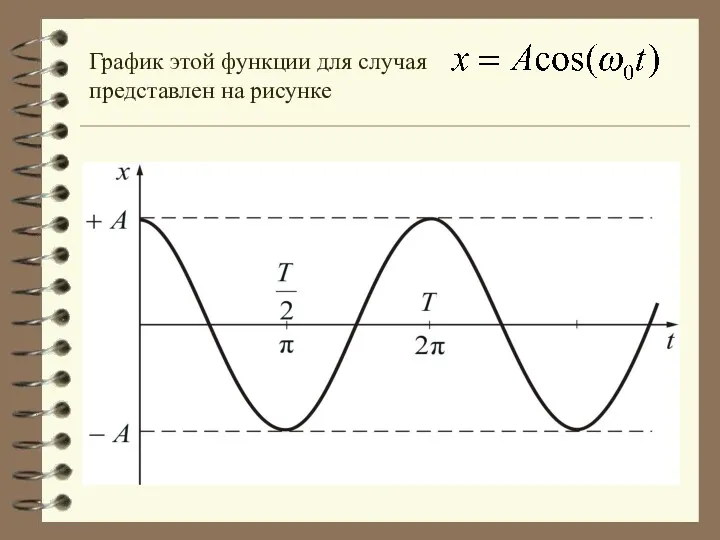
- 16. График этой функции для случая представлен на рисунке
- 17. Определенные состояния системы, совершающей гармонические колебания, повторяются через промежуток времени , называемый периодом колебаний, за который
- 18. Найдем дифференциальное уравнение, которое описывает гармонические колебания. Для этого вычислим производные функции по времени. Первая производная
- 19. Скорость , ускорение. Согласно определению, первая производная от по времени является скоростью: Вторая производная - ускорением:
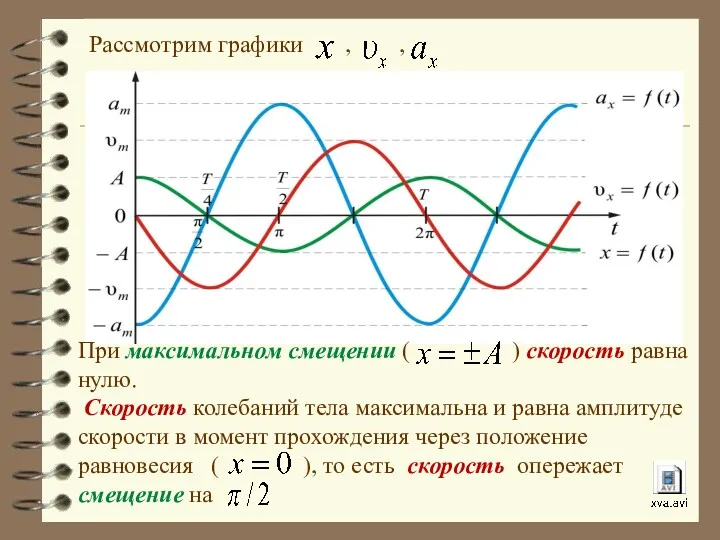
- 20. Рассмотрим графики , , При максимальном смещении ( ) скорость равна нулю. Скорость колебаний тела максимальна
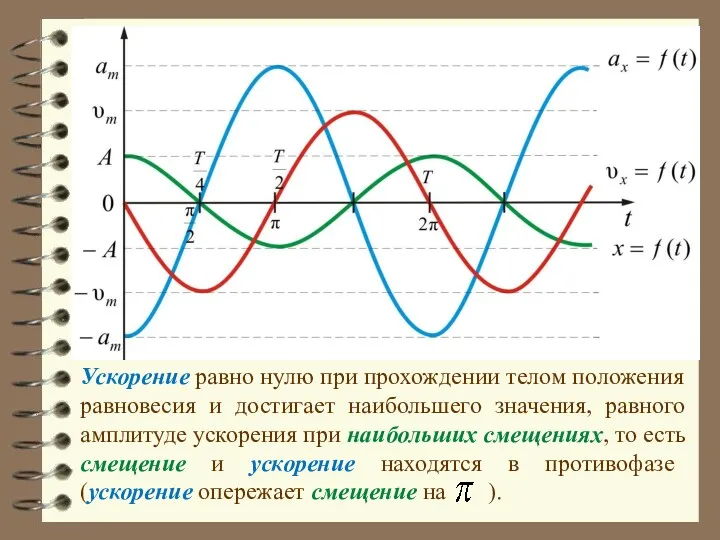
- 21. Ускорение равно нулю при прохождении телом положения равновесия и достигает наибольшего значения, равного амплитуде ускорения при
- 22. Основное уравнение динамики гармонических колебаний Исходя из второго закона, , можно записать: сила F пропорциональна х
- 23. Сравнивая , видим, что Получим основное уравнение динамики гармонических колебаний, вызываемых упругими силами: ; ; Основное
- 24. Круговая частота колебаний , но так как , то Период колебаний груза на пружине:
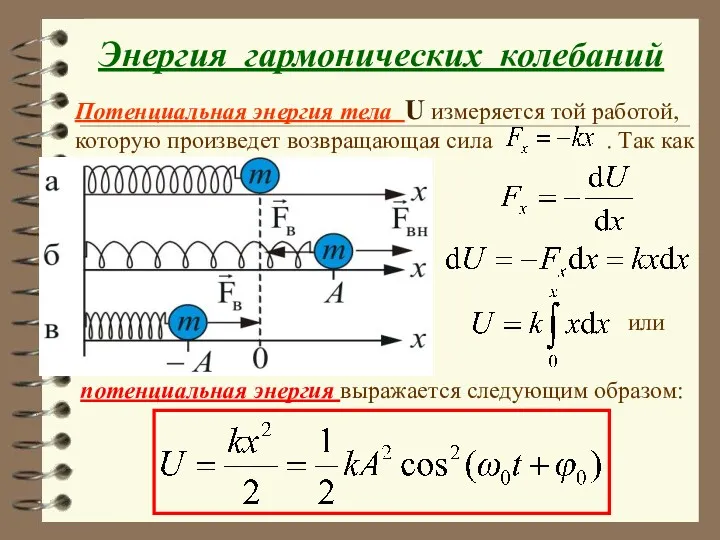
- 25. Энергия гармонических колебаний Потенциальная энергия тела U измеряется той работой, которую произведет возвращающая сила . Так
- 26. или Кинетическая энергия или Из формул, приведенных в рамках следует, что U и K изменяются с
- 27. Сложив выражения для U и K, получим формулу для полной энергии: Полная энергия остается постоянной, так
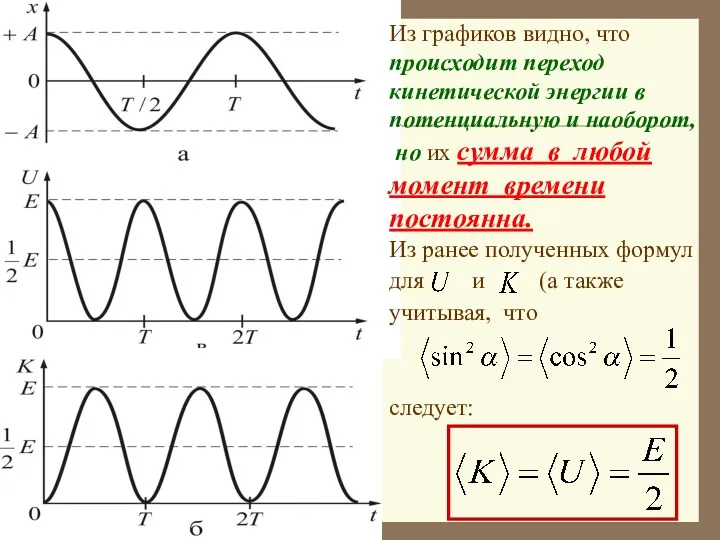
- 28. Из графиков видно, что происходит переход кинетической энергии в потенциальную и наоборот, но их сумма в
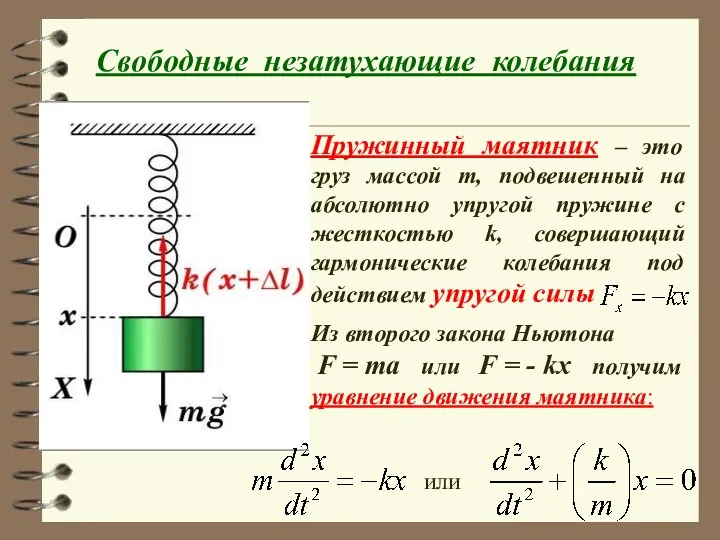
- 29. Свободные незатухающие колебания Пружинный маятник – это груз массой m, подвешенный на абсолютно упругой пружине с
- 30. Решение этого уравнения – гармонические колебания вида: циклическая частота период
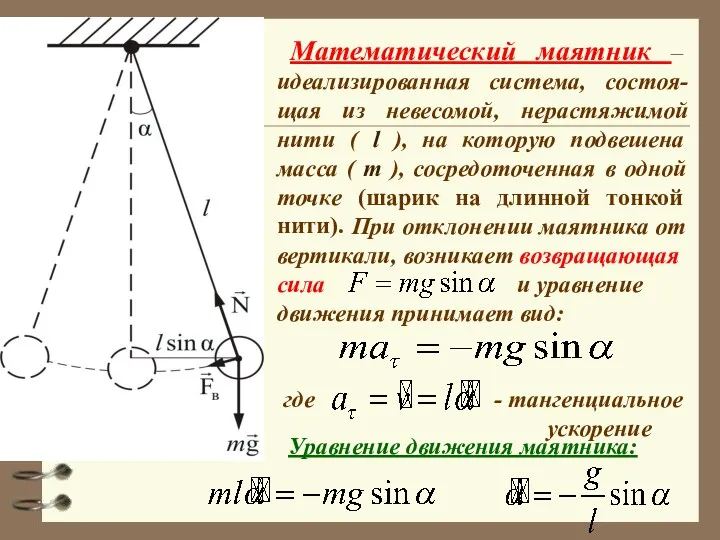
- 31. Математический маятник – идеализированная система, состоя-щая из невесомой, нерастяжимой нити ( l ), на которую подвешена
- 32. Так как рассматриваются только малые отклонения ( ), уравнение движения маятника: Решение этого уравнения - гармонические
- 34. СЛОЖЕНИЕ ГАРМОНИЧЕСКИХ КОЛЕБАНИЙ ОДНОГО НАПРАВЛЕНИЯ И ОДИНАКОВОЙ ЧАСТОТЫ Колеблющееся тело может участвовать в нескольких колебательных процессах.
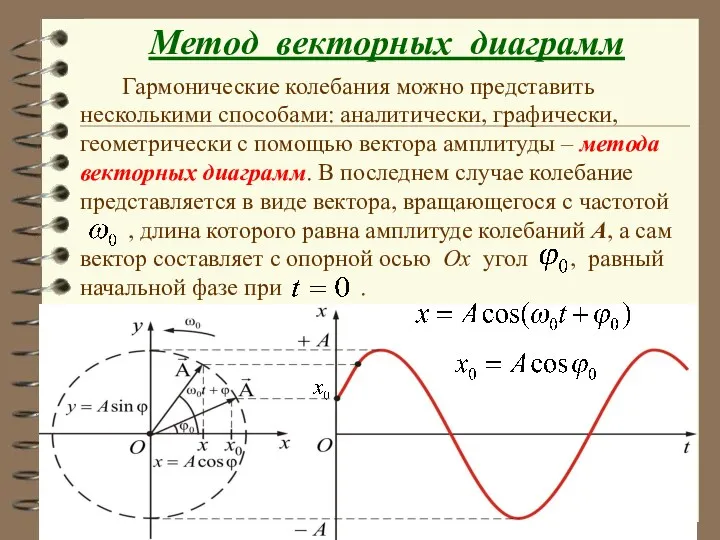
- 35. Метод векторных диаграмм Гармонические колебания можно представить несколькими способами: аналитически, графически, геометрически с помощью вектора амплитуды
- 36. Проекция этого вектора на ось Ox описывает гармоничес-кое колебание Пусть точка одновременно участвует в двух гармонических
- 37. По правилу сложения векторов найдем суммарную амплитуду, результирующего колебания: Начальная фаза результирующего колебания определяется из соотношения:
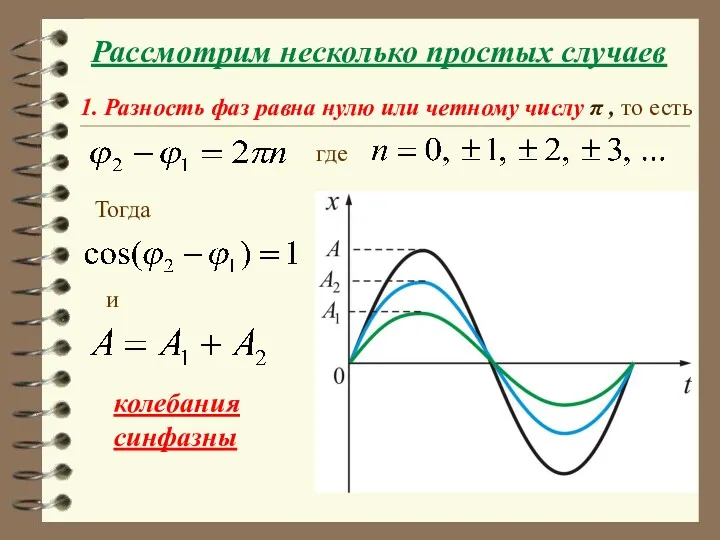
- 38. Рассмотрим несколько простых случаев 1. Разность фаз равна нулю или четному числу π , то есть
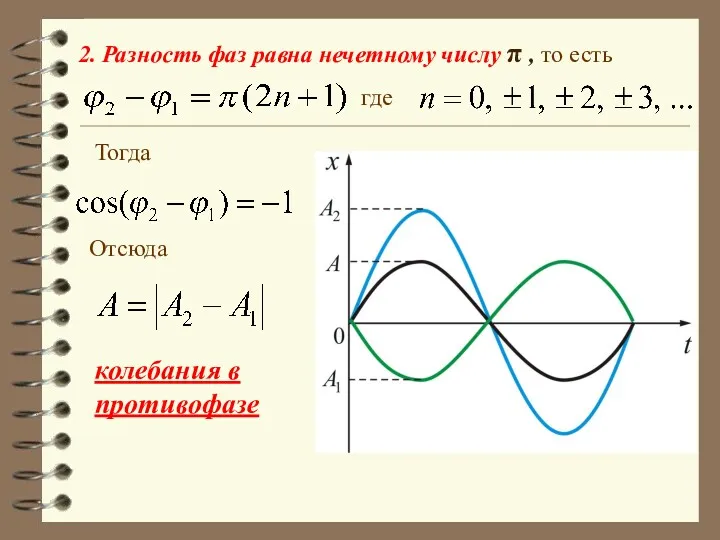
- 39. 2. Разность фаз равна нечетному числу π , то есть где Тогда Отсюда колебания в противофазе
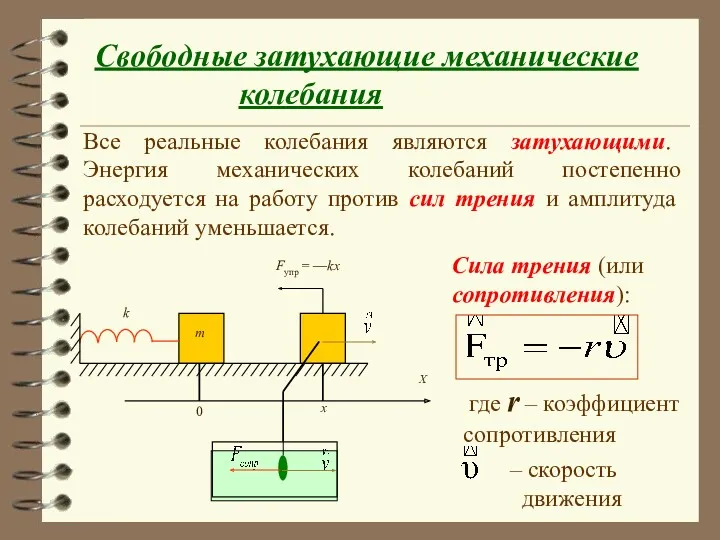
- 40. Свободные затухающие механические колебания Все реальные колебания являются затухающими. Энергия механических колебаний постепенно расходуется на работу
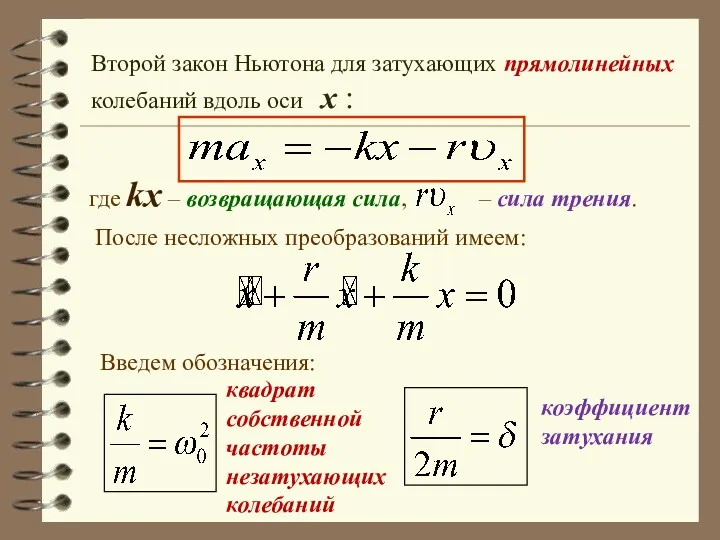
- 41. Второй закон Ньютона для затухающих прямолинейных колебаний вдоль оси x : где kx – возвращающая сила,
- 42. Дифференциальное уравнение свободных затухающих колебаний: Решение этого уравнения (при ) имеет вид: Частота колебаний: Условный период:
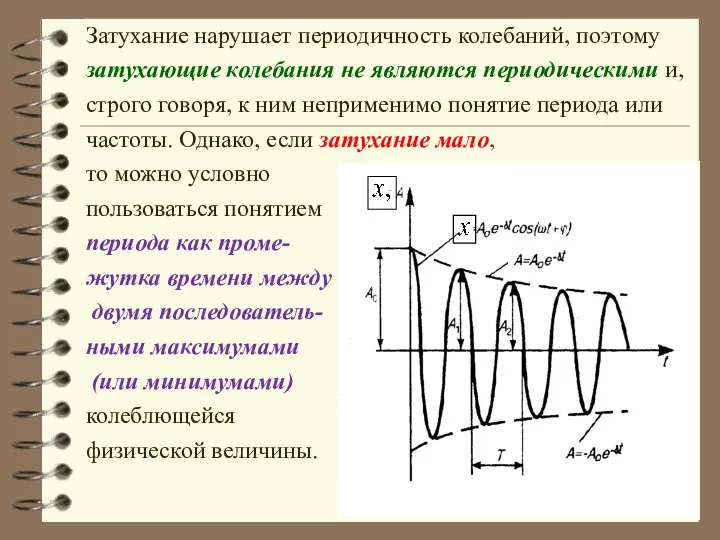
- 43. Затухание нарушает периодичность колебаний, поэтому затухающие колебания не являются периодическими и, строго говоря, к ним неприменимо
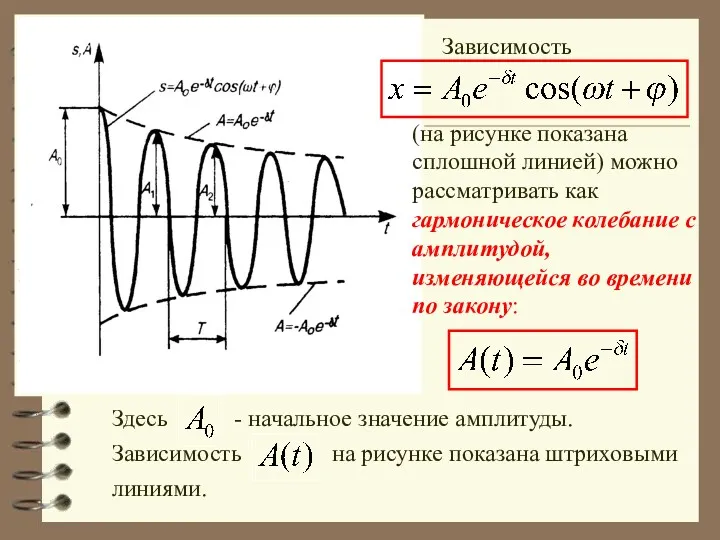
- 44. Зависимость (на рисунке показана сплошной линией) можно рассматривать как гармоническое колебание с амплитудой, изменяющейся во времени
- 45. Основные параметры (характеристики) затухающих колебаний Время релаксации - - время, за которое амплитуда уменьшается в раз.
- 46. Логарифмическим декрементом затухания d называется натуральный логарифм отношения амплитуд, следующих друг за другом через период Т.
- 47. Добротность является важнейшей характеристикой колебательной системы, которая при малых значениях коэффициента затухания равна (так как затухание
- 48. При малом затухании: Среднее значение энергии за период: Средняя энергия, которая теряется в единицу времени: Тогда
- 49. Физический смысл добротности: Добротность пропорциональна отношению средней энергии, запасенной осциллятором за период, к средним потерям энергии
- 50. Вынужденные колебания гармонического осциллятора Чтобы в реальной колебательной системе получить незатухающие колебания, надо компенсировать потери энергии.
- 51. Дифференциальное уравнение вынужденных колебаний под действием гармонической силы Рассмотрим систему, на которую кроме упругой силы (–
- 52. Решение уравнения равно сумме общего решения однородного уравнения и частного решения неоднородного уравнения: Где общее решение
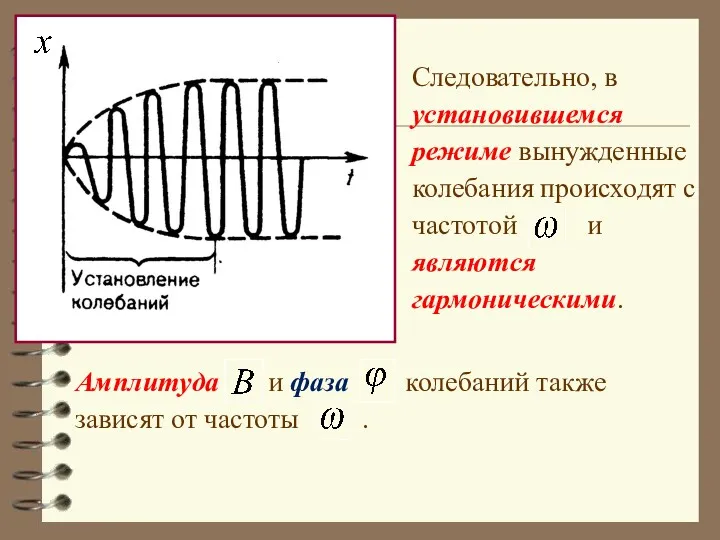
- 53. Итак, частное решение неоднородного уравнения: Слагаемое играет существенную роль только в начальной стадии процесса (при установлении
- 54. Следовательно, в установившемся режиме вынужденные колебания происходят с частотой и являются гармоническими. Амплитуда и фаза колебаний
- 55. Амплитуда и фаза вынужденных колебаний. Резонанс. Рассмотрим зависимость амплитуды вынужденных колебаний от частоты . Из формулы:
- 56. Видно, что амплитуда смещения имеет максимум при некоторой частоте, которую называют резонансной Чтобы определить резонансную частоту,
- 57. Это равенство выполняется при: Физический смысл имеет лишь положительный корень. Следовательно, резонансная частота: Значение резонансной амплитуды:
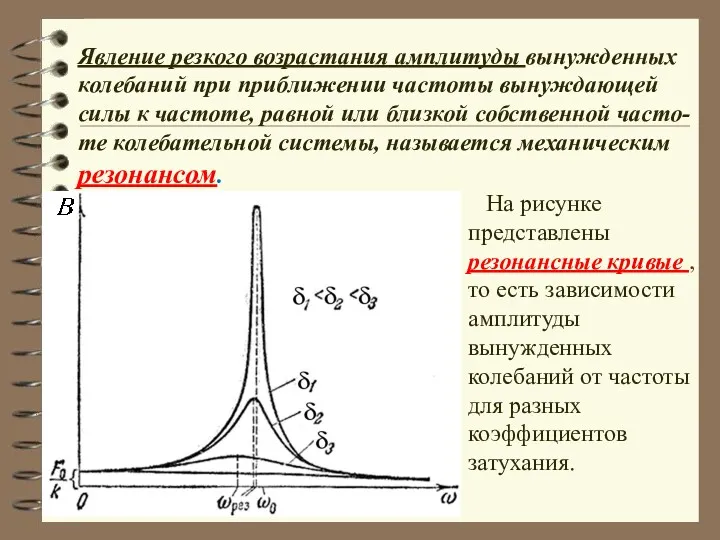
- 58. Явление резкого возрастания амплитуды вынужденных колебаний при приближении частоты вынуждающей силы к частоте, равной или близкой
- 59. При малом затухании: Разделим полученную резонансную амплитуду на статическое смещение системы из положения равновесия под действием
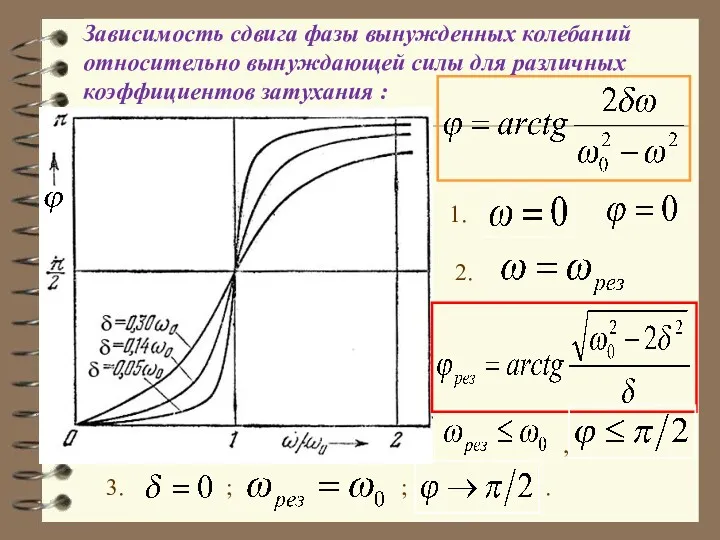
- 60. Зависимость сдвига фазы вынужденных колебаний относительно вынуждающей силы для различных коэффициентов затухания : 1. 2. ,
- 62. Скачать презентацию




































 Газовые законы — повторительно-обобщающий урок
Газовые законы — повторительно-обобщающий урок Двигатель для перспективного самолёта-штурмовика – турбореактивный двигатель Р-195
Двигатель для перспективного самолёта-штурмовика – турбореактивный двигатель Р-195 Линзы. Оптическая сила линзы
Линзы. Оптическая сила линзы Экзамен ПМ 01. Билет № 4. Такелажные работы при монтаже технологического оборудования и трубопроводов
Экзамен ПМ 01. Билет № 4. Такелажные работы при монтаже технологического оборудования и трубопроводов Модель атома водорода Бора . Постулаты Н. Бора. Квантовые генераторы
Модель атома водорода Бора . Постулаты Н. Бора. Квантовые генераторы Исследование свойства воды
Исследование свойства воды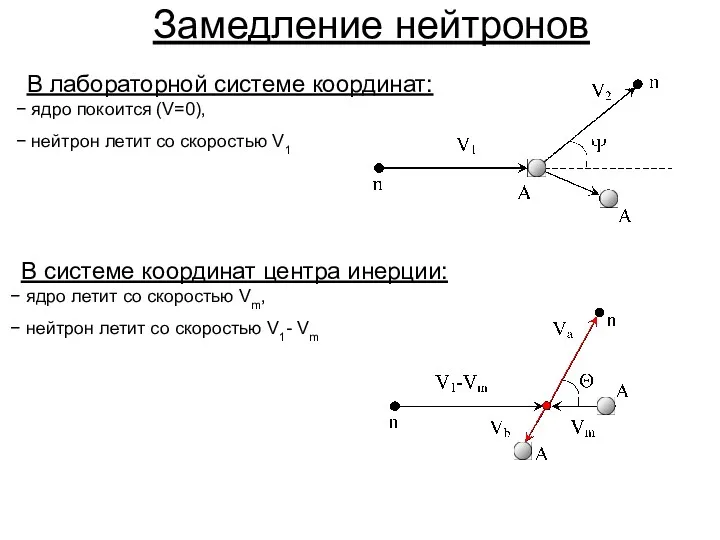 Замедление нейтронов
Замедление нейтронов Электрическое поле и его напряженность. Принцип суперпозиции полей точечных зарядов
Электрическое поле и его напряженность. Принцип суперпозиции полей точечных зарядов Система зажигания
Система зажигания ИКТ как средство повышения эффективности урока
ИКТ как средство повышения эффективности урока Подвеска в автомобиле. Типы подвесок
Подвеска в автомобиле. Типы подвесок Что называется массой тела?
Что называется массой тела? Первый закон Ньютона
Первый закон Ньютона Фотоэффеќт, или фотоэлектрический эффект
Фотоэффеќт, или фотоэлектрический эффект Електричний струм в рідинах
Електричний струм в рідинах Давление. Действие силы (7 класс)
Давление. Действие силы (7 класс) что вы знаете о лампочке Яблочкова...
что вы знаете о лампочке Яблочкова... Законы трения скольжения
Законы трения скольжения Газовые лазеры
Газовые лазеры Кулон заңы тақырыбына есептер шығару
Кулон заңы тақырыбына есептер шығару Презентация по теме Кинематика механического движения
Презентация по теме Кинематика механического движения Шум как опасный фактор
Шум как опасный фактор Тепловые явления
Тепловые явления урок физики в 7 классе по теме Сила трения
урок физики в 7 классе по теме Сила трения Рационалистическое концепции естественного права
Рационалистическое концепции естественного права Презентация Созвездия
Презентация Созвездия Электроборудование пассажирских вагонов
Электроборудование пассажирских вагонов Измерение сопротивления при помощи мостовой схемы
Измерение сопротивления при помощи мостовой схемы