Механические гармонические колебания. §1. Колебательное движение. Признаки и условия колебательного движения презентация
Содержание
- 2. §1 Колебательное движение. Признаки и условия колебательного движения. Примеры колебаний Пружинный маятник Математический маятник Физический маятник
- 3. По физической природе колебания подразделяются: Биологические Социальные Космологические и т.п. Механические Электромеханические Электромагнитные
- 4. Признаки колебания: Наличие равновесного состояния в системе. Непрерывная изменяемость скорости V и силы F по величине
- 5. Условия колебательного движения: Наличие Fупр (или Fквазиупр) силы, направленной к положению равновесия (возвращающая сила). Система должна
- 6. §2 Кинематика и динамика гармонического колебательного движения Рассмотрим пружинный маятник и модель гармонического колебания на примере
- 7. Эти выражения являются уравнениями гармонического движения. Их вывод можно осуществить на основе анализа динамики колебания тела.
- 8. Решение этого дифференциального уравнения имеет вид: (6) – это уравнение описывает кинематику гармонического движения, где ω0
- 9. Кинематические характеристики колебания: У (или Х) – смещение – это линейное отклонение точки от положения равновесия;
- 10. §3 Колебания математического и физического маятников – примеры свободных гармонических колебаний а) Математический маятник – система,
- 11. Решением уравнения (12) будет выражение: (13) Таким образом, уравнение (13) указывает, что движение гармоническое, подчиняющееся закону
- 12. Момент силы М определяет по 2-му закону Ньютона угловое ускорение–ε, т.е. (17), но далее: – дифференциальное
- 13. §4 Энергия гармонического колебания Полная механическая энергия при гармоническом колебании в общем случае состоит из кинетической
- 15. Скачать презентацию
 Термоядерная реакция. 9 класс
Термоядерная реакция. 9 класс Передачи гибкой связью. Цепные передачи. Классификация
Передачи гибкой связью. Цепные передачи. Классификация Технічне обслуговування електрообладнання автомобілів та системи запалювання карбюраторних двигунів (6)
Технічне обслуговування електрообладнання автомобілів та системи запалювання карбюраторних двигунів (6)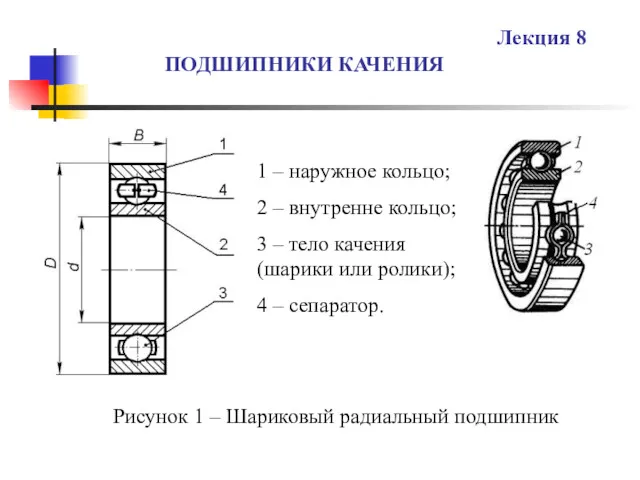 Подшипники качения. (Лекция 8)
Подшипники качения. (Лекция 8) Нейтронный цикл в ядерном реакторе
Нейтронный цикл в ядерном реакторе Школа экспериментов. Занятие 3
Школа экспериментов. Занятие 3 Урок по теме Сила трения 7 класс
Урок по теме Сила трения 7 класс Подшипники качения
Подшипники качения Гидродинамика Солнца. (Лекция 6)
Гидродинамика Солнца. (Лекция 6) Общее устройство автомобиля
Общее устройство автомобиля Кинематика материальной точки
Кинематика материальной точки Электронный парамагнитный резонанс
Электронный парамагнитный резонанс Магнитное поле Земли
Магнитное поле Земли Биологиялық жүйелер
Биологиялық жүйелер Взаимодействие рентгеновского излучения с веществом
Взаимодействие рентгеновского излучения с веществом Термодинамика. Законы термодинамики
Термодинамика. Законы термодинамики Адаптация обучающихся в учебном пространстве предмета - физика
Адаптация обучающихся в учебном пространстве предмета - физика Презентация к методической разработке Проектная и исследовательская деятельность на уроках физики
Презентация к методической разработке Проектная и исследовательская деятельность на уроках физики Допуски и посадки. Взаимозаменяемость
Допуски и посадки. Взаимозаменяемость Пространственная система сил
Пространственная система сил Механическая работа и энергия. Тема 4
Механическая работа и энергия. Тема 4 Презентация к уроку физики в 9 классе по теме Искусственные спутники Земли. Первая космическая скорость
Презентация к уроку физики в 9 классе по теме Искусственные спутники Земли. Первая космическая скорость Old Polish cars
Old Polish cars Испарение. Поглощение энергии при испарении и выделение её при конденсации пара
Испарение. Поглощение энергии при испарении и выделение её при конденсации пара Устройство увеличительных приборов и правила работы с ними
Устройство увеличительных приборов и правила работы с ними урок в 8 классе. Решение задач по теме равномерное прямолинейное движение.
урок в 8 классе. Решение задач по теме равномерное прямолинейное движение. Система запуска
Система запуска