Содержание
- 2. Параметры гармонических колебаний Период (Т) - время, в течении которого совершается одно полное колебание: 1. Гармонические
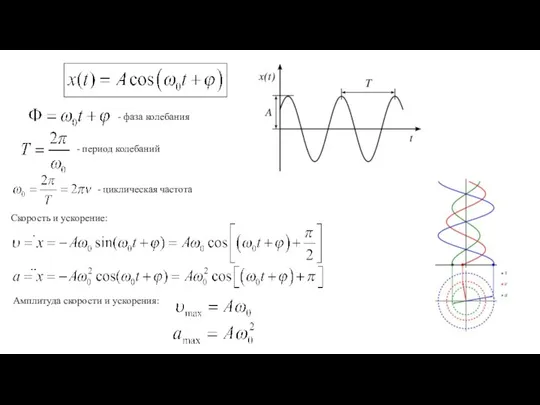
- 3. Гармонические колебания - колебания, при которых изменение величины происходит по закону синуса или косинуса: - значение
- 4. 2. Свободные незатухающие механические колебания: Свободные или собственные колебания - колебания, которые совершает система около положения
- 6. Пружинный маятник - материальная точка массой m, подвешенная на абсолютно упругой невесомой пружине и совершающая колебания
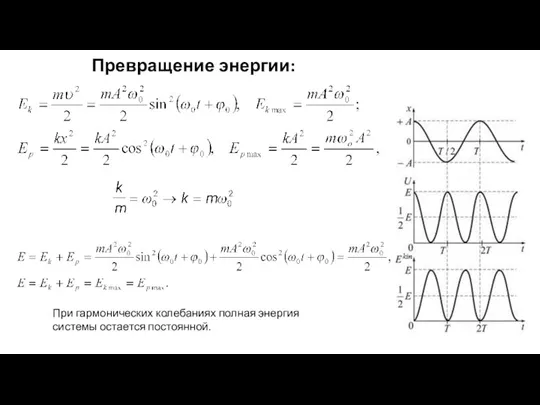
- 7. Превращение энергии: При гармонических колебаниях полная энергия системы остается постоянной.
- 8. - фаза колебания - циклическая частота Скорость и ускорение: - период колебаний Амплитуда скорости и ускорения:
- 9. Математический маятник - материальная точка, подвешенная на невесомой нерастяжимой нити. Период колебаний математического маятника: Основной закон
- 10. Пружинный и математический маятники являются гармоническими осцилляторами (как и колебательный контур). Гармоническим осциллятором называется система, описываемая
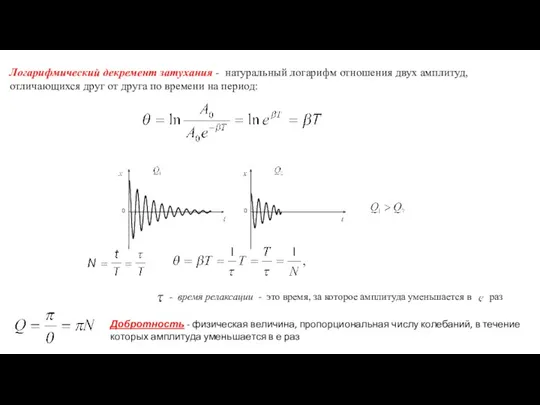
- 11. 4. Свободные затухающие механические колебания. Затухающие колебания - это колебания, амплитуда которых убывает со временем. дифференциальное
- 12. Логарифмический декремент затухания - натуральный логарифм отношения двух амплитуд, отличающихся друг от друга по времени на
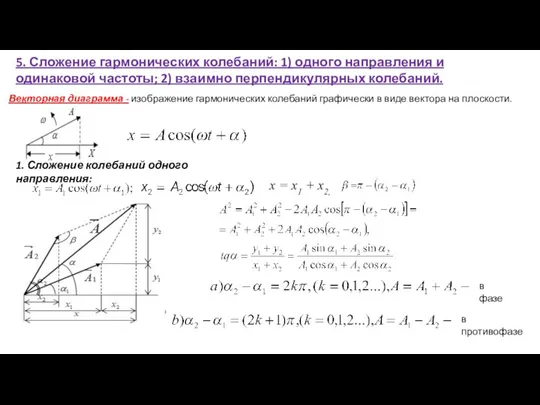
- 13. 5. Сложение гармонических колебаний: 1) одного направления и одинаковой частоты; 2) взаимно перпендикулярных колебаний. Векторная диаграмма
- 14. 2. Сложение взаимно перпендикулярных колебаний: Пусть оба колебания совершаются с одинаковой частотой: Исключим время и свяжем
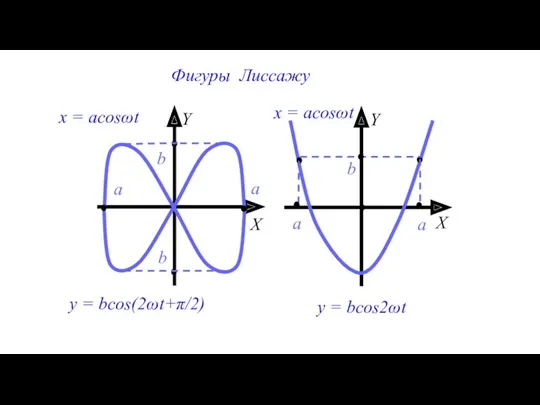
- 15. уравнение прямой уравнение эллипса - уравнение окружности 3. Если складываются взаимно перпендикулярные колебания с кратными периодами,
- 16. X Y a a b b x = acosωt y = bcos(2ωt+π/2) X Y a a
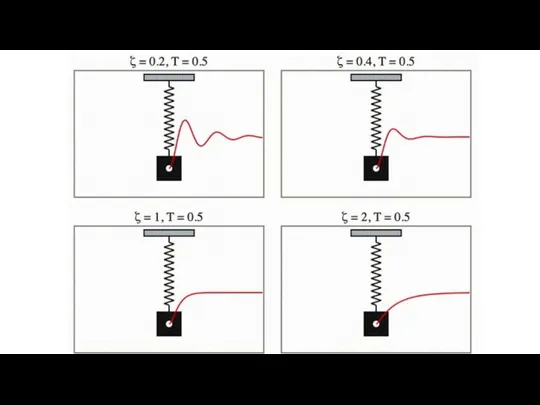
- 17. 6. Вынужденные колебания. Резонанс. Пусть внешняя сила изменяется по гармоническому закону: дифференциальное уравнение вынужденных гармонических колебаний
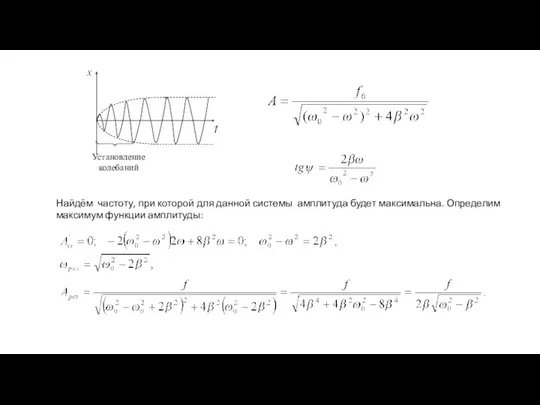
- 18. Найдём частоту, при которой для данной системы амплитуда будет максимальна. Определим максимум функции амплитуды:
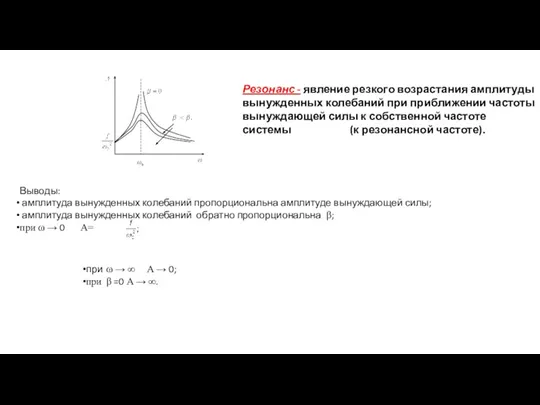
- 19. Резонанс - явление резкого возрастания амплитуды вынужденных колебаний при приближении частоты вынуждающей силы к собственной частоте
- 20. 7. Продольные и поперечные упругие волны. Принцип Гюйгенса. Упругая волна - процесс распространения механических колебаний в
- 21. Упругая волна называется поперечной, если частицы среды колеблются перпендикулярно направлению распространения волны. Поперечная волна возможна в
- 22. Фронт волны - геометрическое место точек, до которых распространились колебания к данному моменту времени t. Волновая
- 23. Уравнение плоской бегущей волны. Бегущими называются волны, которые переносят в пространстве энергию. Получим уравнение бегущей плоской
- 25. Скачать презентацию














 Расчетный напор НС-2 при расположении башни в начале сети
Расчетный напор НС-2 при расположении башни в начале сети Жас физик
Жас физик В мире оптических иллюзий
В мире оптических иллюзий Коливання
Коливання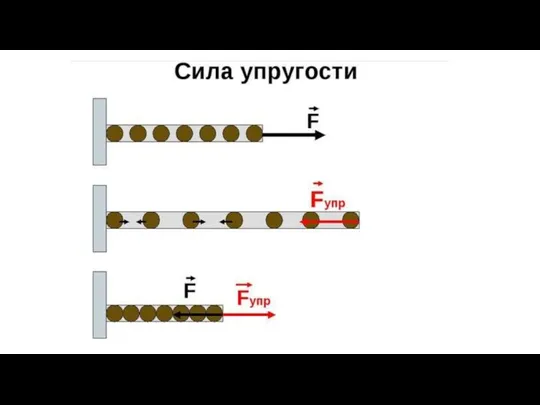 Сила упругости
Сила упругости Громкость звука. 9 класс
Громкость звука. 9 класс Определение перемещений сечений стержневых систем
Определение перемещений сечений стержневых систем Электростатическое поле в вакууме
Электростатическое поле в вакууме Магнит өрісі
Магнит өрісі Радиоволны
Радиоволны Магнитное поле и его графическое изображение. Неоднородное и однородное магнитное поле
Магнитное поле и его графическое изображение. Неоднородное и однородное магнитное поле Светильники с лампами ДРЛ: сервисное обслуживание и ремонт. Монтаж, наладка и испытания
Светильники с лампами ДРЛ: сервисное обслуживание и ремонт. Монтаж, наладка и испытания Электрическое поле в вакууме. Лекция 1
Электрическое поле в вакууме. Лекция 1 Магниторазведка. Магнетизм и магнетики
Магниторазведка. Магнетизм и магнетики Основы кинематики и динамики. Кинематика точки
Основы кинематики и динамики. Кинематика точки Радио. История и изобретение радио
Радио. История и изобретение радио Время
Время Урок физики 8 класс Испарение и конденсация
Урок физики 8 класс Испарение и конденсация Тушение пожара. Проект ORGLAG-01 (Мобильная платформа с системой огнетушения)
Тушение пожара. Проект ORGLAG-01 (Мобильная платформа с системой огнетушения) Простые механизмы
Простые механизмы Закон сохранения механической энергии. Работа силы. Мощность
Закон сохранения механической энергии. Работа силы. Мощность Оптическое волокно как диэлектрический волновод
Оптическое волокно как диэлектрический волновод Презентация к уроку по теме Простые механизмы.
Презентация к уроку по теме Простые механизмы. Технические измерения. Допуски и посадки гладких цилиндрических соединений деталей (гцс)
Технические измерения. Допуски и посадки гладких цилиндрических соединений деталей (гцс) Вещества и явления в окружающем мире
Вещества и явления в окружающем мире Свободные электрические колебания. Электричество и магнетизм
Свободные электрические колебания. Электричество и магнетизм Тепловые явления
Тепловые явления Закон сохранения энергии. Адиабатический процесс
Закон сохранения энергии. Адиабатический процесс