Содержание
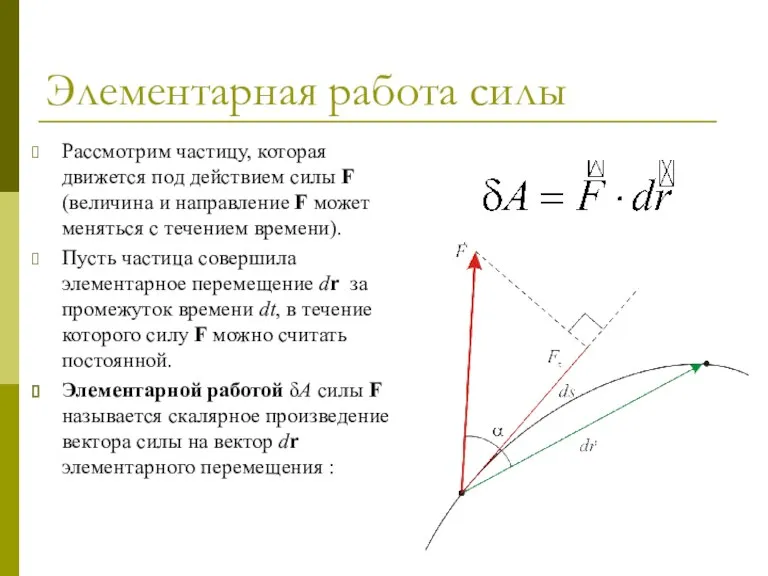
- 2. Элементарная работа силы Рассмотрим частицу, которая движется под действием силы F (величина и направление F может
- 3. Элементарная работа силы Элементарную работу можно представить в другой форме: Здесь α – угол между векторами
- 4. Элементарная работа силы В декартовой прямоугольной системе координат элементарную работу силы F можно представить в виде
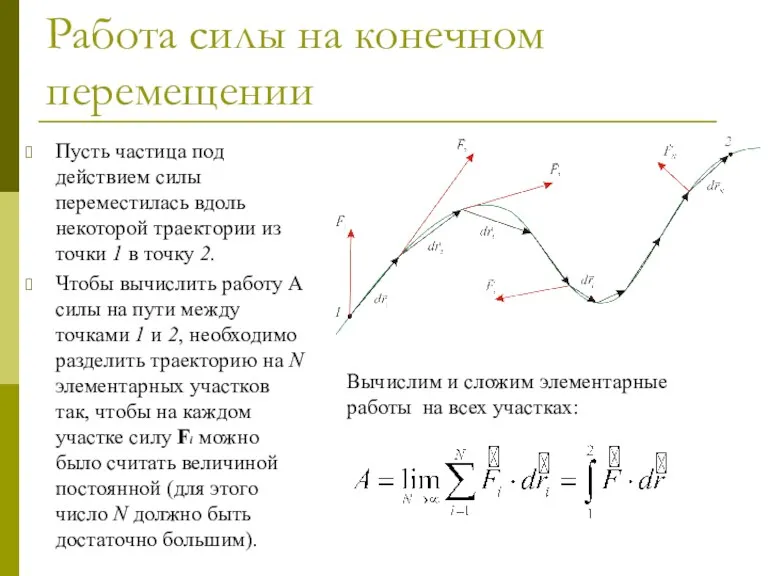
- 5. Работа силы на конечном перемещении Пусть частица под действием силы переместилась вдоль некоторой траектории из точки
- 6. Работа силы на конечном перемещении Таким образом, работа A силы F на конечном пути равна Единицей
- 7. Принцип суперпозиции работ Если действующую на частицу силу можно представить в виде векторной суммы нескольких составляющих:
- 8. Мощность Мощность – это скалярная физическая величина, которая характеризует работу силы, произведенную в единицу времени. Пусть
- 9. Мощность Мгновенную мощность можно выразить через скорость v движения частицы и действующую на нее силу F:
- 10. Мощность Выразим работу A силы на конечном пути через мгновенную мощность P: С учетом этого соотношения,
- 11. ЗАКОН СОХРАНЕНИЯ МЕХАНИЧЕСКОЙ ЭНЕРГИИ Вычисление работы сил в механике
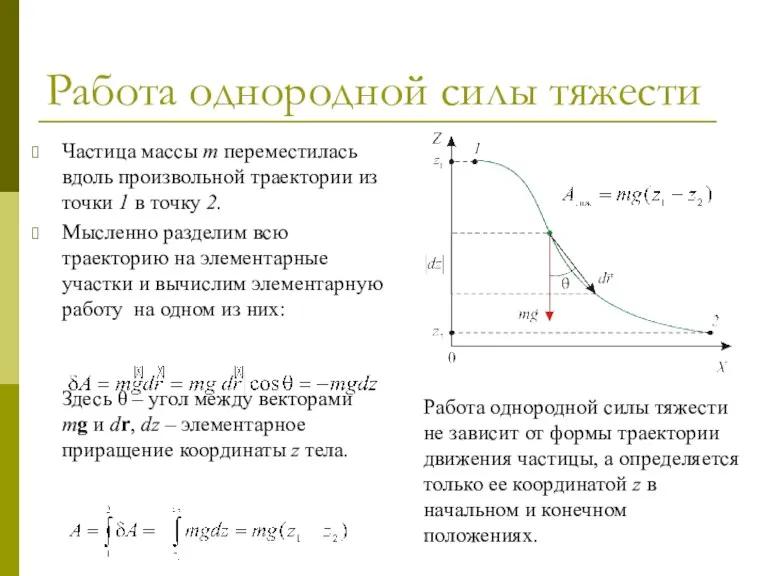
- 12. Работа однородной силы тяжести Частица массы m переместилась вдоль произвольной траектории из точки 1 в точку
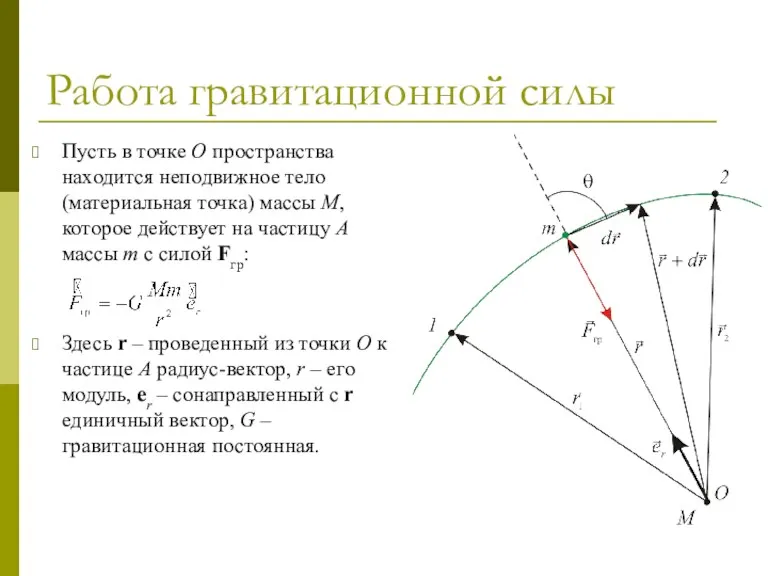
- 13. Работа гравитационной силы Пусть в точке O пространства находится неподвижное тело (материальная точка) массы M, которое
- 14. Работа гравитационной силы Элементарная работа гравитационной силы: Здесь величина dr = |dr|cosθ приблизительно равна приращению dr
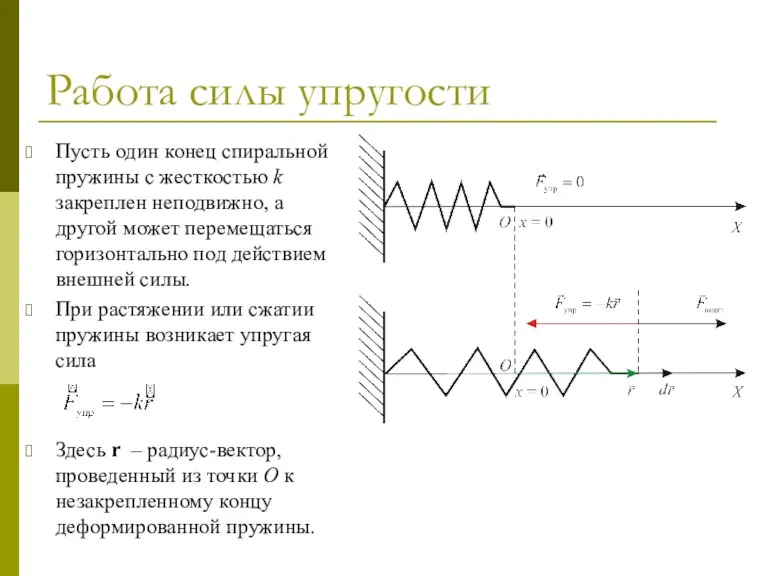
- 15. Работа силы упругости Пусть один конец спиральной пружины с жесткостью k закреплен неподвижно, а другой может
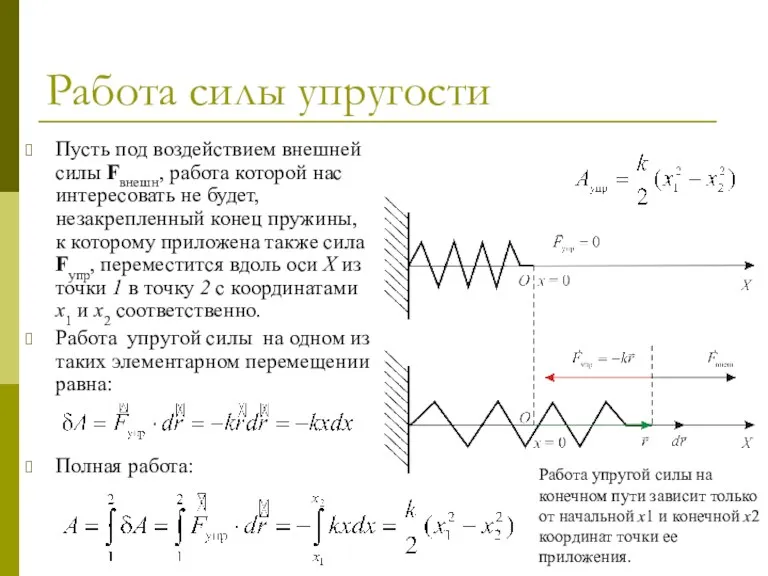
- 16. Работа силы упругости Пусть под воздействием внешней силы Fвнешн, работа которой нас интересовать не будет, незакрепленный
- 17. ЗАКОН СОХРАНЕНИЯ МЕХАНИЧЕСКОЙ ЭНЕРГИИ Кинетическая энергия частицы и системы частиц
- 18. Кинетическая энергия частицы Пусть частица массы m движется со скоростью v. Кинетической энергией частицы называется величина:
- 19. Кинетическая энергия системы частиц Кинетическая энергия системы частиц, массы которых m1, m2, …, mi, …, mN,
- 20. Теорема о кинетической энергии частицы Пусть частица массы m движется под действием некоторой силы F (равнодействующая
- 21. Доказательство теоремы о кинетической энергии частицы Работа силы F на элементарном перемещении dr равна: Тогда
- 22. Теорема о кинетической энергии системы частиц Теорема о кинетической энергии для системы частиц. При переходе системы
- 23. Доказательство теоремы о кинетической энергии системы частиц Работа A всех приложенных к частицам сил равна сумме
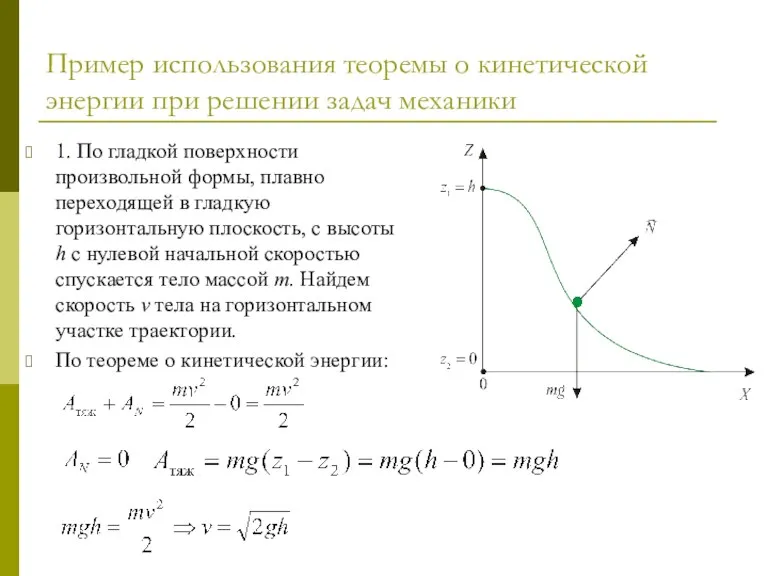
- 24. Пример использования теоремы о кинетической энергии при решении задач механики 1. По гладкой поверхности произвольной формы,
- 25. ЗАКОН СОХРАНЕНИЯ МЕХАНИЧЕСКОЙ ЭНЕРГИИ
- 26. Силовое поле Если на частицу в каждой точке пространства действует определенная сила, то всю совокупность сил
- 27. Силовые линии поля Силовой линией поля называется линия в пространстве, касательная к которой в каждой точке
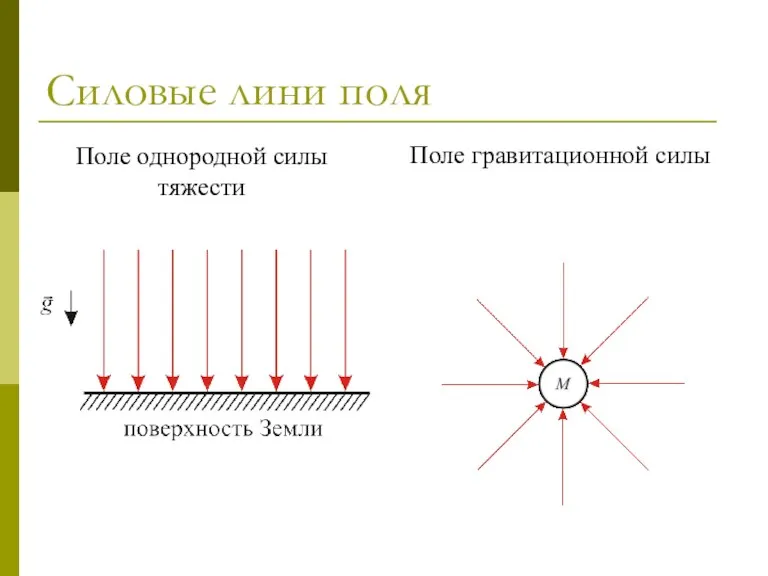
- 28. Силовые лини поля Поле однородной силы тяжести Поле гравитационной силы
- 29. Консервативные силы Консервативным называется поле, в котором совершаемая при перемещении частицы из произвольного начального в произвольное
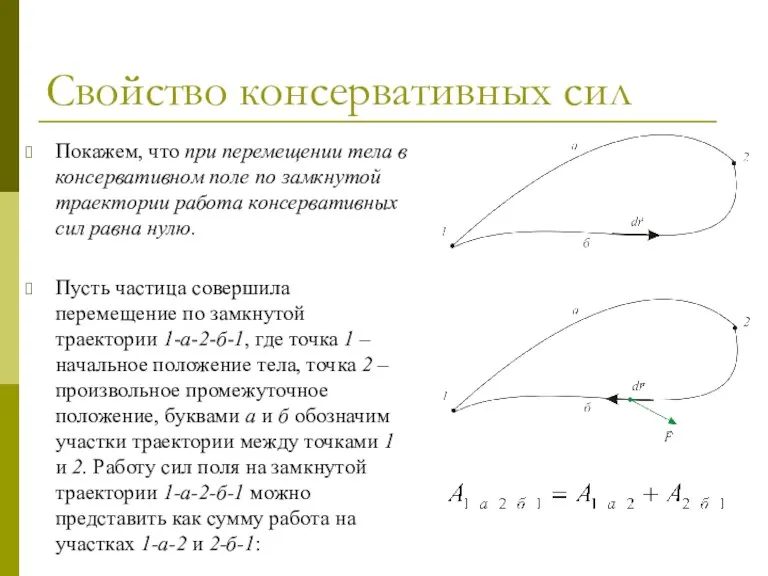
- 30. Свойство консервативных сил Покажем, что при перемещении тела в консервативном поле по замкнутой траектории работа консервативных
- 31. Работа консервативной силы при движении по замкнутой траектории Работа сил поля при перемещении частиц из точки
- 32. Потенциальная энергия частицы Рассмотрим консервативное поле. Частица расположена в точке P поля с координатами x, y,
- 33. Свойства потенциальной энергии частицы 1. Потенциальная энергия является функцией только координат x, y, z точки поля,
- 34. Свойства потенциальной энергии частицы 2. Работа сил поля при перемещении частицы из произвольного начального в произвольное
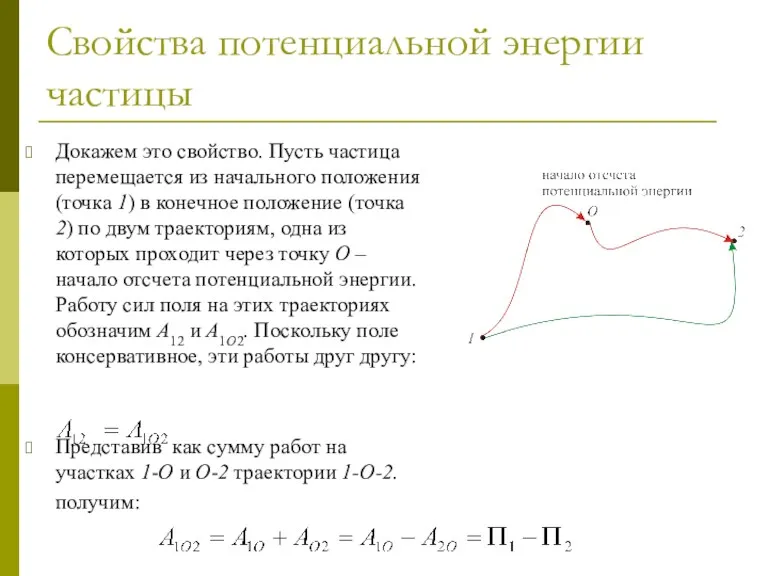
- 35. Свойства потенциальной энергии частицы Докажем это свойство. Пусть частица перемещается из начального положения (точка 1) в
- 36. Свойства потенциальной энергии частицы 3. Потенциальная энергия частицы определена с точностью до произвольной постоянной величины. Поясним
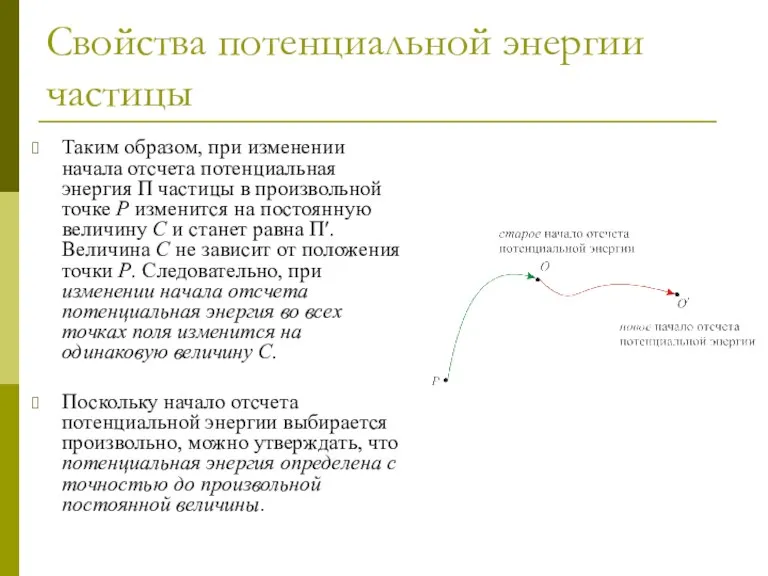
- 37. Свойства потенциальной энергии частицы Таким образом, при изменении начала отсчета потенциальная энергия Π частицы в произвольной
- 39. Скачать презентацию

























 Решение задач. Закон всемирного тяготения.
Решение задач. Закон всемирного тяготения. Мир физики
Мир физики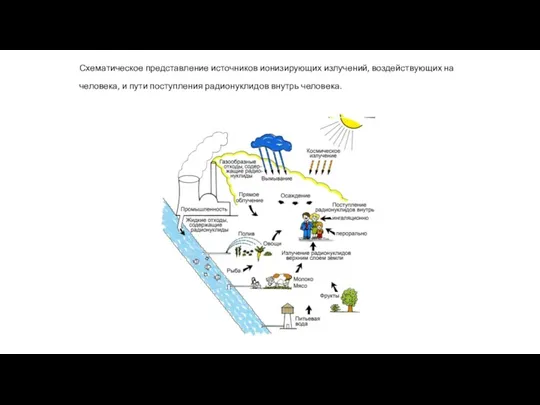 Схематическое представление источников ионизирующих излучений, воздействующих на человека
Схематическое представление источников ионизирующих излучений, воздействующих на человека Сборка неподвижных и неразъемных соединений деталей
Сборка неподвижных и неразъемных соединений деталей Типовые схемные решения объемных гидроприводов
Типовые схемные решения объемных гидроприводов Постоянные магниты
Постоянные магниты Уравнение состояния идеального газа. Газовые законы
Уравнение состояния идеального газа. Газовые законы Пленки Лэнгмюра-Блоджетт
Пленки Лэнгмюра-Блоджетт Презентация Лабораторная работа №2 Измерение размеров малых тел 7 класс
Презентация Лабораторная работа №2 Измерение размеров малых тел 7 класс Сварные детали машин. Особенности проектирования и изготовления сварных деталей машин в машиностроении
Сварные детали машин. Особенности проектирования и изготовления сварных деталей машин в машиностроении Керамикалық, Электрлік оқшаулама материалдар
Керамикалық, Электрлік оқшаулама материалдар Преломление света. 8 класс
Преломление света. 8 класс Сходства и различия микро- и макромира
Сходства и различия микро- и макромира Электрическое освещение. Лекция 3
Электрическое освещение. Лекция 3 AdvPh mirrors
AdvPh mirrors Сложное сопротивление
Сложное сопротивление Электроемкость. Конденсаторы
Электроемкость. Конденсаторы Физика для любознательных
Физика для любознательных Әр түрлі иондаушы сәулелер көздері түрлерінің заттармен өзара әсерлесуі
Әр түрлі иондаушы сәулелер көздері түрлерінің заттармен өзара әсерлесуі Кристаллофизикалық координат жүйесі
Кристаллофизикалық координат жүйесі Паровые машины
Паровые машины Решение задач по теме Динамика. 10 класс
Решение задач по теме Динамика. 10 класс Виды машинных швов
Виды машинных швов Водород – главный элемент галактики
Водород – главный элемент галактики Транспортная энергетика. Теплопередача. (Лекция 9)
Транспортная энергетика. Теплопередача. (Лекция 9) Зачетная работа по физике
Зачетная работа по физике Эхометод измерения глубины
Эхометод измерения глубины Кампания ядерного реактора
Кампания ядерного реактора