Содержание
- 2. Вопросы лекции Пример использования метацентрической формулы Остойчивость веса и формы Условия и меры начальной остойчивости судна
- 3. Знание, понимание и профессиональные навыки в соответствии с минимальным стандартом компетентности для вахтенных помощников капитана судов
- 4. Знание, понимание и профессиональные навыки в соответствии с минимальным стандартом компетентности для капитанов и старших помощников
- 5. 1. Пример использования метацентрической формулы
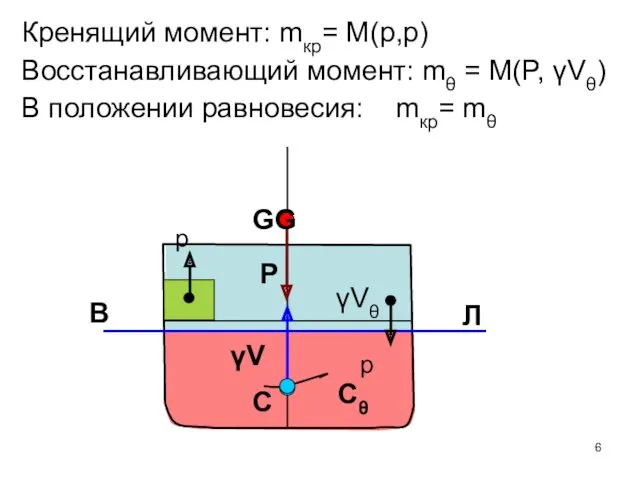
- 6. В Л Cθ C γVθ P γV Кренящий момент: mкр= M(p,p) Восстанавливающий момент: mθ = M(P,
- 7. Наклонение судна Кренование проводится для уточнения нагрузки судна При креновании судно наклоняют, перемещая с борта на
- 8. Данные о судне и крен-балласте Водоизмещение судна Δ = 42000 т Поперечная МЦВ (расчетная) h =
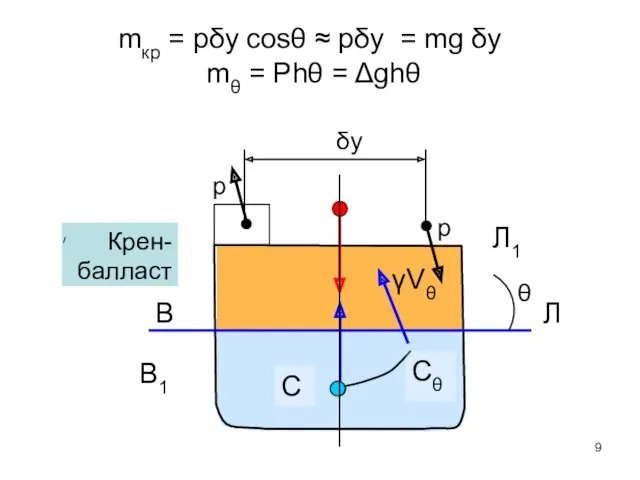
- 9. В Л C Cθ γVθ δy θ mкр = pδy cosθ ≈ pδy = mg δy
- 10. mθ = mкр Подставив выражения для моментов:
- 11. 2. Остойчивость веса и формы
- 12. Две составляющие восстанавливающего момента: Момент остойчивости веса зависит от расположения ЦТ и ЦВ судна до наклонения
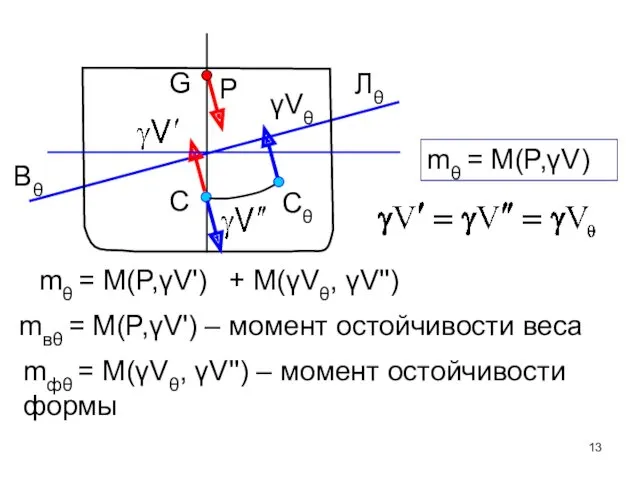
- 13. Cθ C γVθ P Вθ Лθ G mθ = M(P,γV') mвθ = M(P,γV') – момент остойчивости
- 14. Момент остойчивости веса mвθ ЦТ судна всегда лежит выше, чем ЦВ Момент остойчивости веса всегда отрицателен
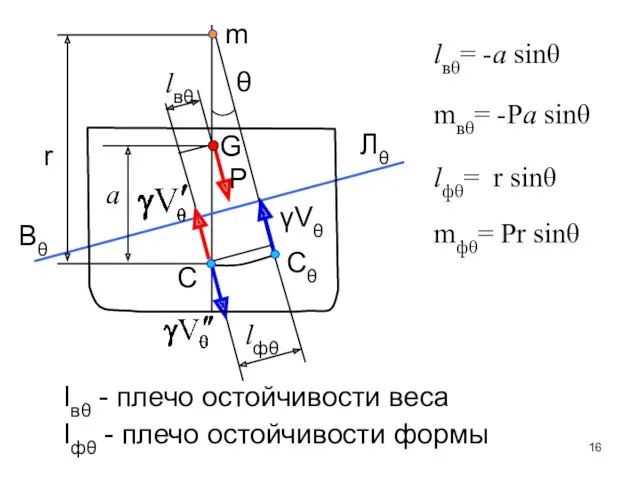
- 15. Момент остойчивости формы mфθ Момент остойчивости формы зависит от смещения центра величины судна при наклонении Смещение
- 16. Cθ m θ lвθ lфθ lвθ= -a sinθ mвθ= -Pa sinθ lфθ= r sinθ mфθ= Pr
- 17. mфθ= Pr sinθ P = γV, mфθ= γIx sinθ Чем шире ватерлиния, тем больше Ix ,
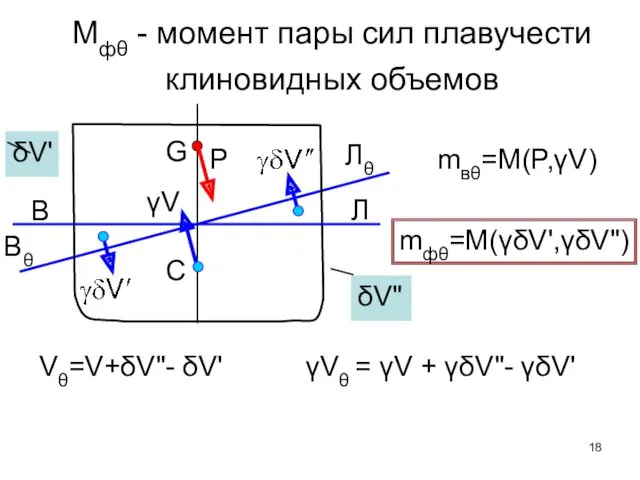
- 18. P γV δV" δV' Vθ=V+δV"- δV' γVθ = γV + γδV"- γδV' mвθ=M(P,γV) mфθ=M(γδV',γδV") Mфθ -
- 19. В эксплуатационных условиях углы крена и дифферента, приобретаемые судами, невелики: sinθ = θ и sinψ =
- 20. Роль остойчивости веса и формы a = zg-zc и r = zm-zc - близки по величине
- 21. При изменении осадки mфθ изменяется мало На mвθ влияет только количество и распределение грузов на судне
- 22. 3. Условия и меры начальной остойчивости судна
- 23. 3.1 Условие начальной остойчивости судна
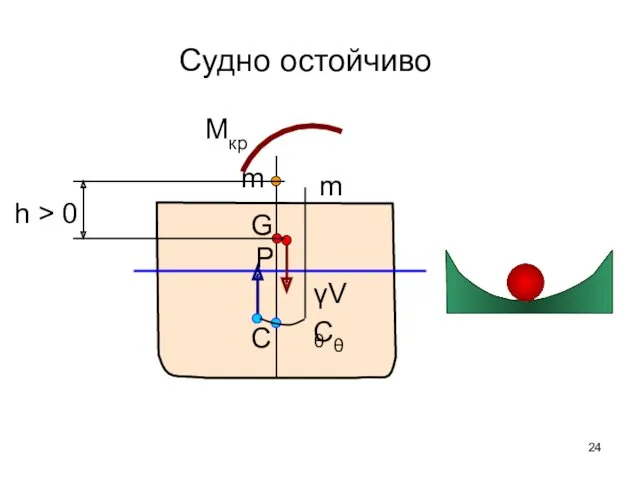
- 24. Судно остойчиво m Cθ G P γVθ m C h > 0 Мкр
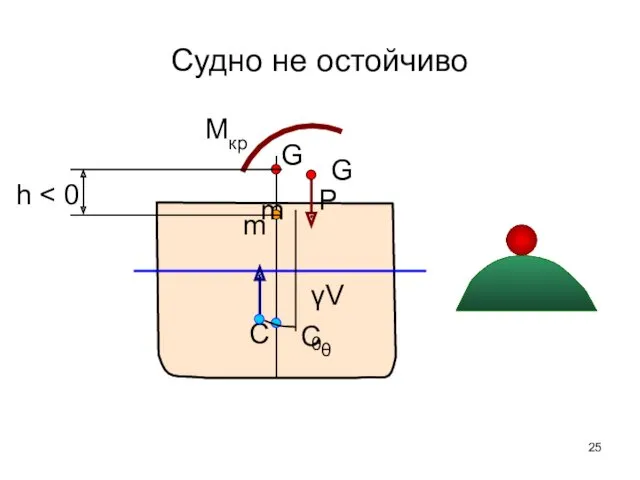
- 25. Судно не остойчиво m Cθ G P γVθ m C h Мкр G
- 26. Условие статической остойчивости судна В данном положении равновесия судно остойчиво, если соответствующая этому положению поперечная метацентрическая
- 27. 3.2 Меры начальной остойчивости
- 28. Меры начальной остойчивости- её численные характеристики: Абсолютные меры начальной остойчивости зависят от величины водоизмещения Относительные меры
- 29. Абсолютные меры начальной остойчивости 1. Коэффициенты статической остойчивости:
- 30. Абсолютные меры начальной остойчивости 2. Моменты, кренящие судно на 1° и дифферентующие судно на 1 см:
- 31. Относительные меры начальной остойчивости Метацентрические высоты – это отношение коэффициентов статической остойчивости к силе тяжести судна
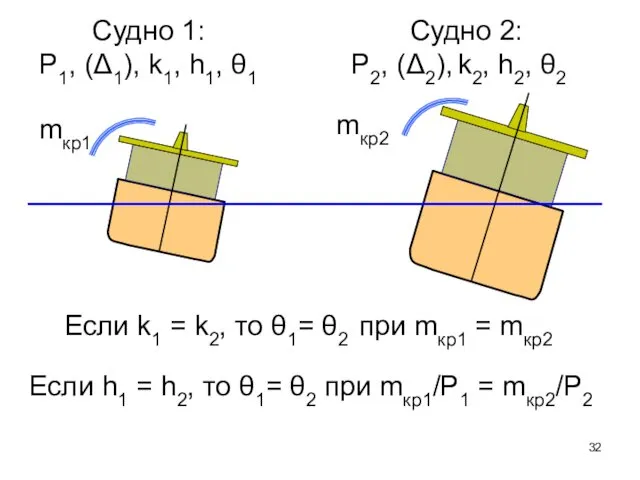
- 32. Судно 1: P1, (Δ1), k1, h1, θ1 Судно 2: P2, (Δ2), k2, h2, θ2 mкр1 mкр2
- 33. Метацентрические высоты и коэффициенты статической остойчивости Если у двух судов k1 = k2, при воздействии одинаковых
- 34. Задание для самостоятельной работы: Теория судна. Статика п.п. 2.6 и 2.7
- 36. Скачать презентацию






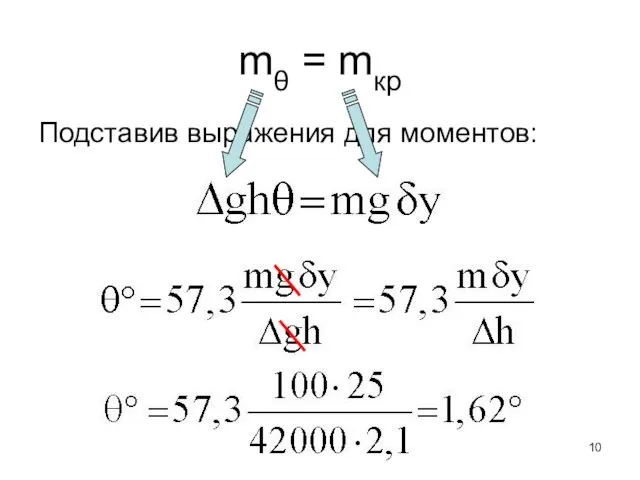


















 Лампа накаливания. Электронагревательные приборы
Лампа накаливания. Электронагревательные приборы Lubrication
Lubrication Закон электромагнитной индукции
Закон электромагнитной индукции Принцип работы, устройство ,техническое обслуживание и ремонт ведущего моста ЗИЛ-130
Принцип работы, устройство ,техническое обслуживание и ремонт ведущего моста ЗИЛ-130 Закон Ома для полной цепи
Закон Ома для полной цепи Ядерная энергетика
Ядерная энергетика Особенности расчета прямозубых конических передач
Особенности расчета прямозубых конических передач Гипотеза де Бройля
Гипотеза де Бройля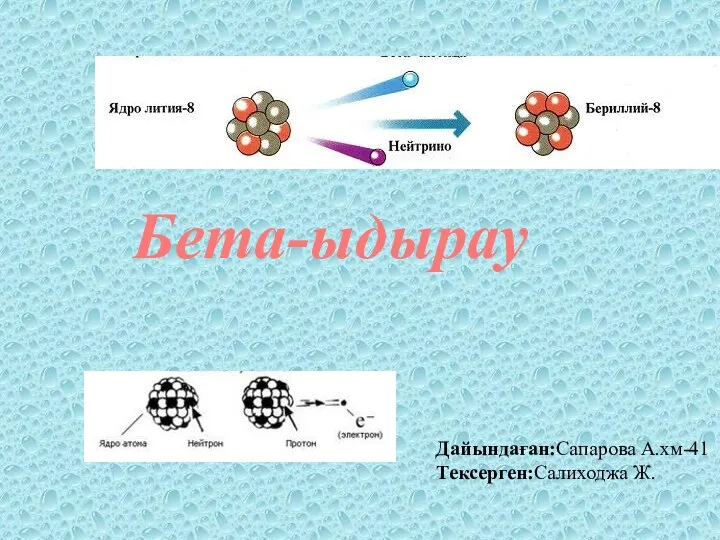 Бета-ыдырау
Бета-ыдырау Лабораторная работа № 7 Измерение работы и мощности тока в электрической лампочке (8 класс)
Лабораторная работа № 7 Измерение работы и мощности тока в электрической лампочке (8 класс) Электродинамика. Электрический заряд и элементарные частицы
Электродинамика. Электрический заряд и элементарные частицы Квантовые свойства света
Квантовые свойства света Балка на упругом основании
Балка на упругом основании Сопротивление материалов. Основные требования к деталям и конструкциям и виды расчетов
Сопротивление материалов. Основные требования к деталям и конструкциям и виды расчетов Основы зонной теории твердого тела
Основы зонной теории твердого тела Оптичні системи. Кут зору
Оптичні системи. Кут зору Матеріали дипломної роботи. Електропостачання житлового мікрорайону міста Дрогобич
Матеріали дипломної роботи. Електропостачання житлового мікрорайону міста Дрогобич Молекулярная физика и основы термодинамики
Молекулярная физика и основы термодинамики Методы изготовления зубчатых колес
Методы изготовления зубчатых колес Спектроскоп. Спектр түрлері
Спектроскоп. Спектр түрлері Lektsia_18_Teplov_izluchen
Lektsia_18_Teplov_izluchen Силовые агрегаты и двигатели
Силовые агрегаты и двигатели Игра Звёдный час по физике 7-8 класс
Игра Звёдный час по физике 7-8 класс История одного трамвая
История одного трамвая КПД простых механизмов. Уроки физики в 7 классе
КПД простых механизмов. Уроки физики в 7 классе Двигатели. Принцип работы и устройство
Двигатели. Принцип работы и устройство Зубчатые передачи с зацеплением
Зубчатые передачи с зацеплением Кинематика. Кинематика точки
Кинематика. Кинематика точки