Содержание
- 2. 2. Кинематика. Векторный способ задания движения точки. Положение точки М задается ее радиусом-вектором , проведенным из
- 3. 3. Кинематика. Координатный способ задания движения точки. Положение точки можно задать ее координатами x, y, z,
- 4. 4. Кинематика. Естественный способ задания движения. Траектория точки М – кривая АВ – известна (рис.38). Точку
- 5. 5. Кинематика. Вектор скорости точки Векторная величина, характеризующая в данный момент быстроту и направление движения по
- 6. 6. Кинематика. Вектор скорости точки. Если промежутки времени малы ( 0) средняя скорость становится равной истинной
- 7. 7. Кинематика. Вектор ускорения точки Ускорением точки называется векторная величина, характеризующая изменение с течением времени модуля
- 8. 8. Кинематика. Скорость и ускорение точки при координатном способе задания движения Воспользуемся теоремой: проекция производной от
- 9. 9. Кинематика. 2. Ускорение точки. Вектор ускорения: Отсюда: , , , или , , . Проекции
- 10. 10. Кинематика. Скорость и ускорение точки при естественном задания движения Даны траектория точки и закон движения
- 11. 11. Кинематика. Скорость и ускорение точки при естественном задании движения. Поскольку вектор скорости точки совпадает с
- 12. 12. Кинематика. Касательное и нормальное ускорение точки Проекции вектора на оси , Mn, Mb: , ,
- 13. 13. Кинематика. Касательное и нормальное ускорения точки Нормальное ускорение характеризует изменение скорости по направлению и определяется:
- 14. 14. Кинематика. Касательное и нормальное ускорения точки. Рис.43.
- 15. 15. Кинематика. Частные случаи движения точки. 1. Прямолинейное движение. , , . Касательное ускорение характеризует изменение
- 16. 16. Кинематика. Частные случаи движения точки. 3. Равномерное прямолинейное движение. , . Ускорение точки равно нулю
- 17. 17. Кинематика. Поступательное движение. Кинематика твердого тела Поступательное движение Поступательным называется такое движение твердого тела, при
- 18. 18. Кинематика. Поступательное движение Поскольку поступательное движение твердого тела определяется движением какой-либо его точки, его движение
- 19. 19. Кинематика. Вращательное движение твердого тела вокруг неподвижной оси. Если твердое тело движется так, что две
- 20. 20. Кинематика. Вращательное движение. Угловая скорость тела определяется: или . Таким образом, числовое значение угловой скорости
- 21. 21. Кинематика. Равномерное вращение Угловая скорость постоянна, т.е. = const . - закон равном. кривол. дв-я
- 22. 22. Кинематика. Определение скоростей и ускорений точек вращающегося тела 1. Скорость точек тела Рис.50. Рис. 51.
- 23. 23. Кинематика. Скорость точек твердого тела при вращательном движении. Скорость точки v называют линейной или окружной
- 24. 24. кинематика. Вращательное движение твердого тела. 2.Ускорение точек тела. Воспользуемся формулами: , , . Тогда, ,
- 25. 25. Кинематика. Ускорение точек тела. Рис.53. Рис.54. Отклонение вектора полного ускорения от радиуса описываемой точкой окружности
- 26. 28. Кинематика. Плоскопараллельное движение. Плоскопараллельное движение твердого тела Плоскопараллельным движением твердого тела называется такое, при котором
- 27. 29. Кинематика. Плоскопараллельное движение твердого тела. На плоскости сечения S проведем отрезок АВ, который и будет
- 28. 30. Кинематика. Плоскопараллельное движение. Основные кинематические характеристики этого движения являются: 1) скорость и ускорение поступательного движения,
- 29. 31. Кинематика. Скорости точек плоской фигуры Скорость любой точки М плоской фигуры геометрически складывается из скорости
- 30. 32. Кинематика. Ускорение точек плоской фигуры Ускорение каждой точки движущейся плоской фигуры равно геометрической сумме двух
- 31. 33. Кинематика. Теорема о проекциях скоростей двух точек тела: Проекции скоростей двух точек твердого тела на
- 32. 34. Кинематика. Мгновенный центр скоростей (МЦС) Изучая движение плоской фигуры в ее поступательном и вращательном движении,
- 33. 35. Кинематика. МЦС. Если Р - полюс, то скорость, например, точки А в момент времени t:
- 34. 36. Кинематика. МЦС. Выводы: 1. Для определения МЦС надо знать только направления скоростей и двух точек
- 35. 37. Кинематика. Частные случаи определения МЦС: 1. При качении без скольжения одного цилиндрического тела по поверхности
- 37. Скачать презентацию
 Основные теоремы электростатики. Тема 2
Основные теоремы электростатики. Тема 2 Электрическая энергия
Электрическая энергия Кинематика кривошипно-шатунного механизма
Кинематика кривошипно-шатунного механизма Архимед күші
Архимед күші Силовой метод функционального диагностирования
Силовой метод функционального диагностирования Своя игра по физике. 9 класс
Своя игра по физике. 9 класс Камера Вильсона
Камера Вильсона Занятие №6. Сложное движение материальной точки
Занятие №6. Сложное движение материальной точки Айнымалы ток генераторы
Айнымалы ток генераторы Научно-исследовательская деятельность как фактор развития личности ученика и роста педагогического мастерства учителя.
Научно-исследовательская деятельность как фактор развития личности ученика и роста педагогического мастерства учителя. Допуски и посадки подшипников качения
Допуски и посадки подшипников качения Сила Лоренца
Сила Лоренца Презентация к уроку Электромагнитные волны в 11 классе
Презентация к уроку Электромагнитные волны в 11 классе Решение задач по теме Строение атома, радиоактивные превращения
Решение задач по теме Строение атома, радиоактивные превращения Дисперсия света
Дисперсия света Презентация 7 кл. Измерение атмосферного давления
Презентация 7 кл. Измерение атмосферного давления Квантовые постулаты Бора
Квантовые постулаты Бора Спин, матрицы Паули
Спин, матрицы Паули Транспортная энергетика. Теплопередача. (Лекция 9)
Транспортная энергетика. Теплопередача. (Лекция 9) Новые средства измерения температуры АО НПП Эталон
Новые средства измерения температуры АО НПП Эталон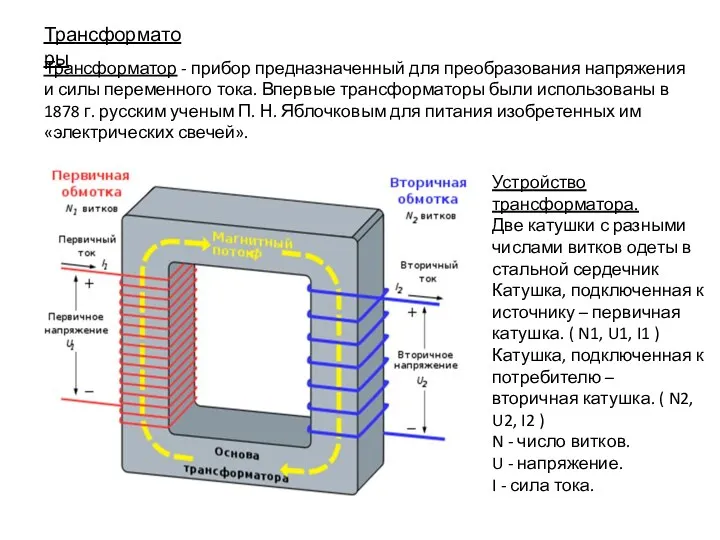 Трансформаторы
Трансформаторы Плоские фермы. Определения. Модель плоской фермы
Плоские фермы. Определения. Модель плоской фермы Молекулярная физика
Молекулярная физика Цепи постоянного тока
Цепи постоянного тока Электрические цепи переменного тока
Электрические цепи переменного тока Некоторые средства развития познавательного интереса на уроках физики 7-8 классов.
Некоторые средства развития познавательного интереса на уроках физики 7-8 классов. Презентация по теме Спектральный анализ и его применение 9 класс
Презентация по теме Спектральный анализ и его применение 9 класс Теплопередача
Теплопередача