Содержание
- 2. Литература: Исаченко В.П., Осипова В.А., Сукомел А.С. Теплопередача, М.: Энергия, 1975. -488 С. Ф. Крейт, У.Блэк
- 3. До сих пор мы рассматривали системы, в которых в результате теплопроводности процессы изменения температуры во времени
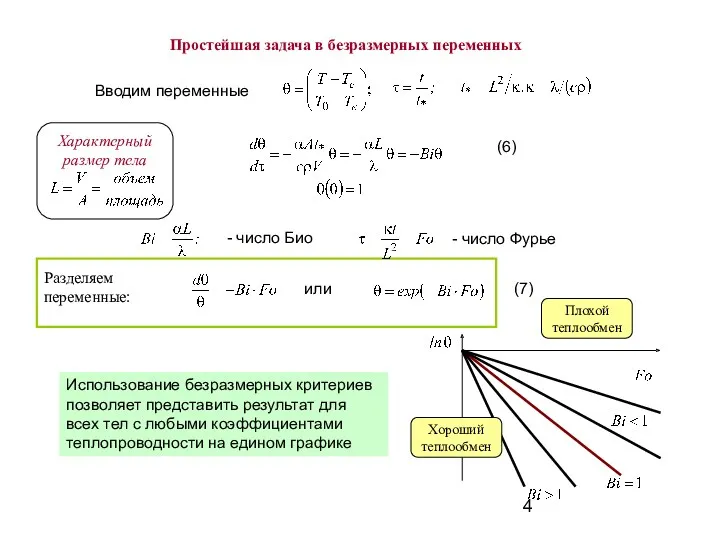
- 4. (6) - число Био - число Фурье или (7) Использование безразмерных критериев позволяет представить результат для
- 6. Пусть теперь граничные условия – функция времени. Примем, что температура потока меняется со временем линейно (
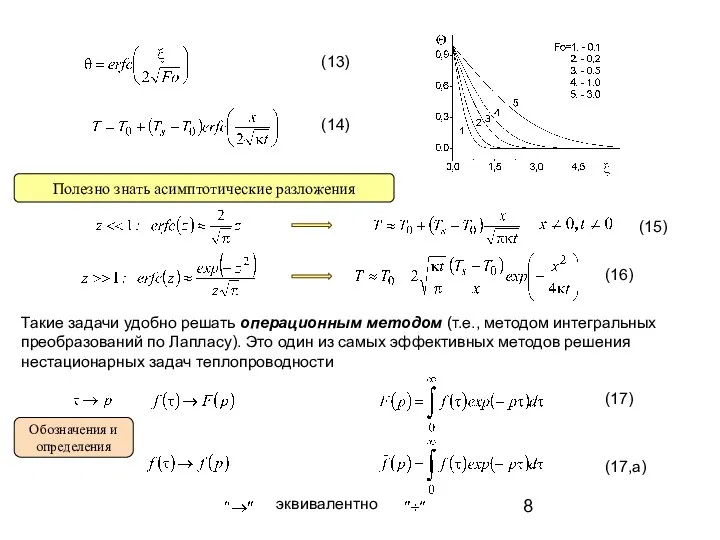
- 9. (11)
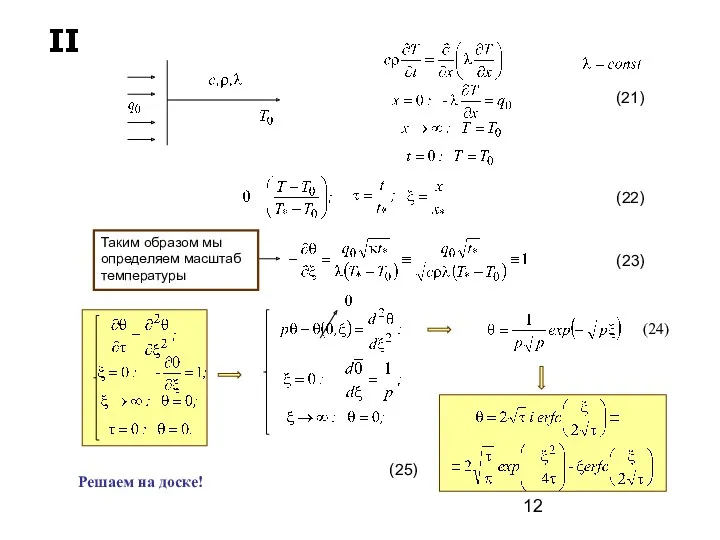
- 12. (22) Таким образом мы определяем масштаб температуры (23) (21) (25) (24) Решаем на доске!
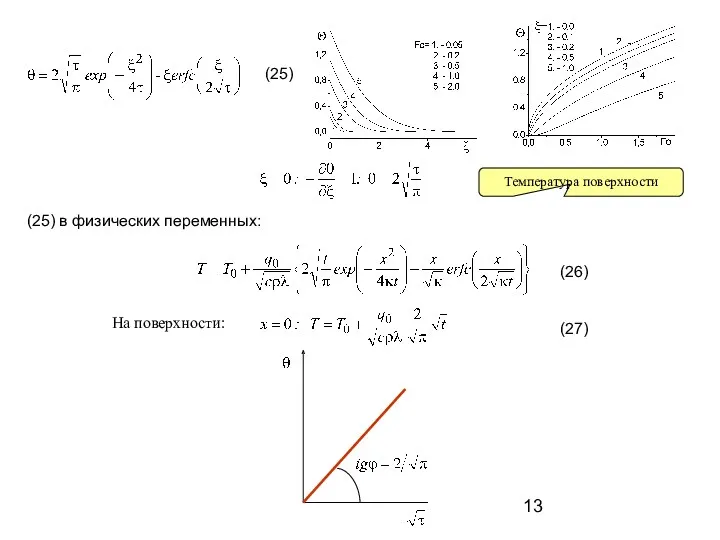
- 13. (25) в физических переменных: (25) (26) (27) Температура поверхности На поверхности:
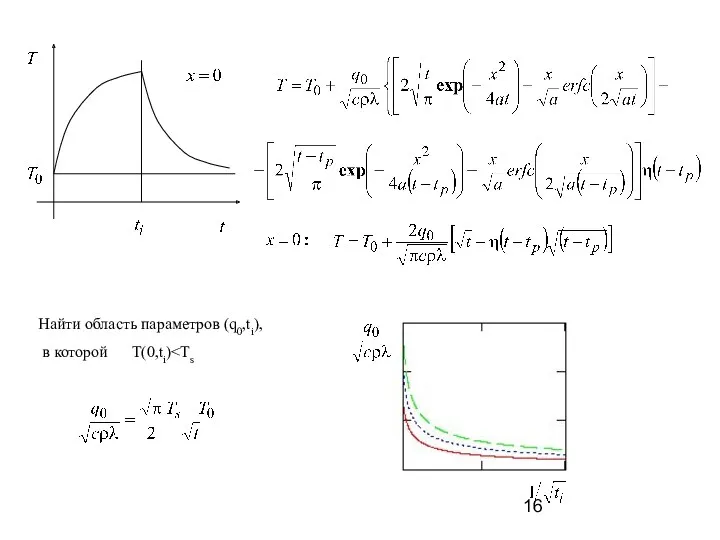
- 14. Граничные условия зависят от времени В пространстве изображений решение будет иметь вид (28) (29) (30) II,a
- 15. Введем новую переменную по формуле Следовательно Подинтегральная функция равна нулю, если
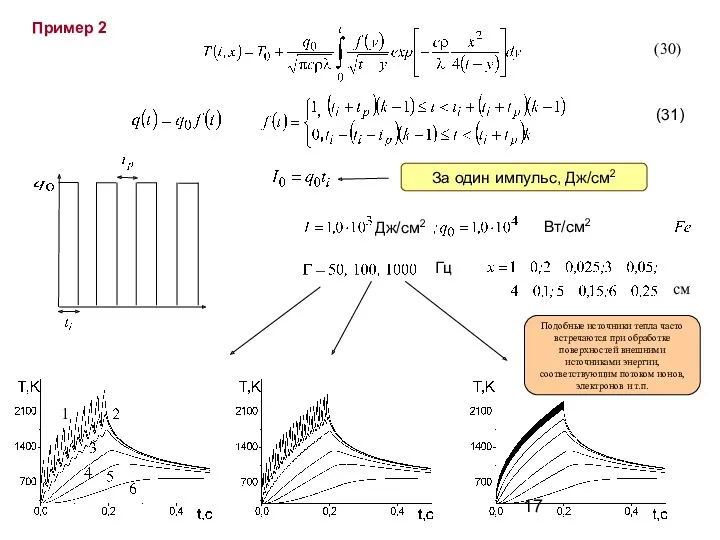
- 17. Пример 2 За один импульс, Дж/см2 Гц (31) см 1 (30) Подобные источники тепла часто встречаются
- 20. Найти решение задачи, используя операционный метод 1.Задача на дом:
- 22. Теорема Дюамеля гласит (37) Теорема Дюамеля может быть применена и к случаям конвективного теплообмена на поверхности,
- 23. (38) Найдем решение для линейного изменения температуры поверхности (40) Мы должны проинтегрировать уравнение (39) Пример
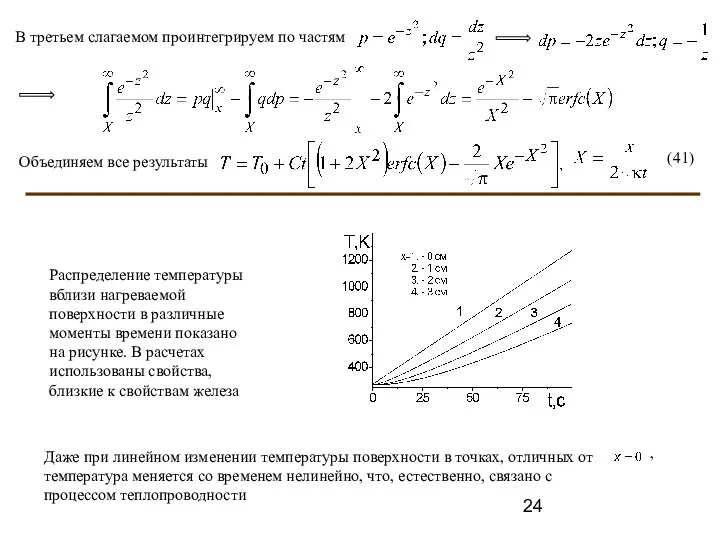
- 24. В третьем слагаемом проинтегрируем по частям Объединяем все результаты (41) Распределение температуры вблизи нагреваемой поверхности в
- 25. (42) Граничные условия такого вида встречаются в поршневых двигателях внутреннего сгорания, циклических регенераторах и наблюдаются в
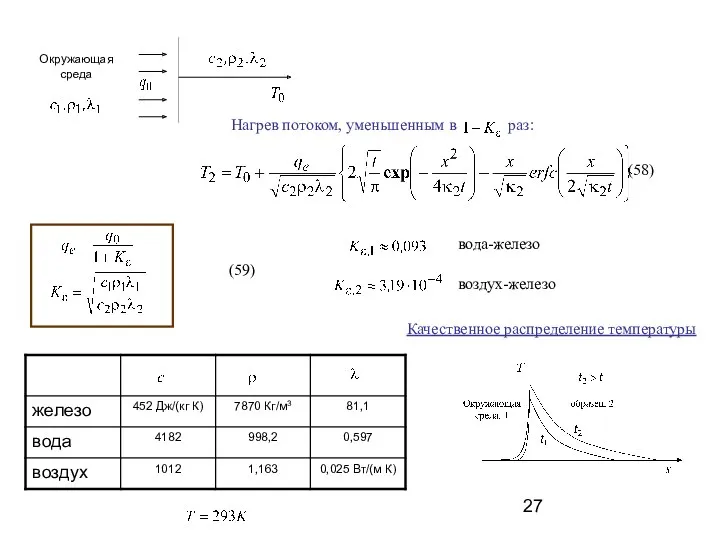
- 27. (58) вода-железо воздух-железо (59) Качественное распределение температуры
- 28. Термическая обработка материала с покрытием
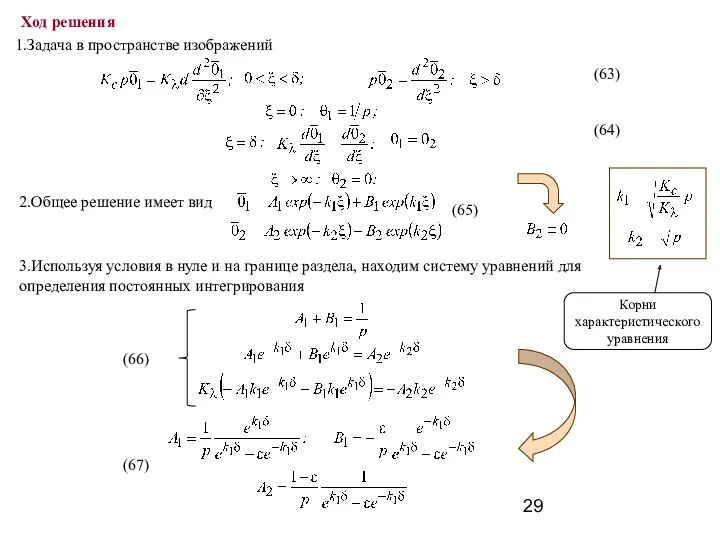
- 29. Ход решения 1.Задача в пространстве изображений 2.Общее решение имеет вид 3.Используя условия в нуле и на
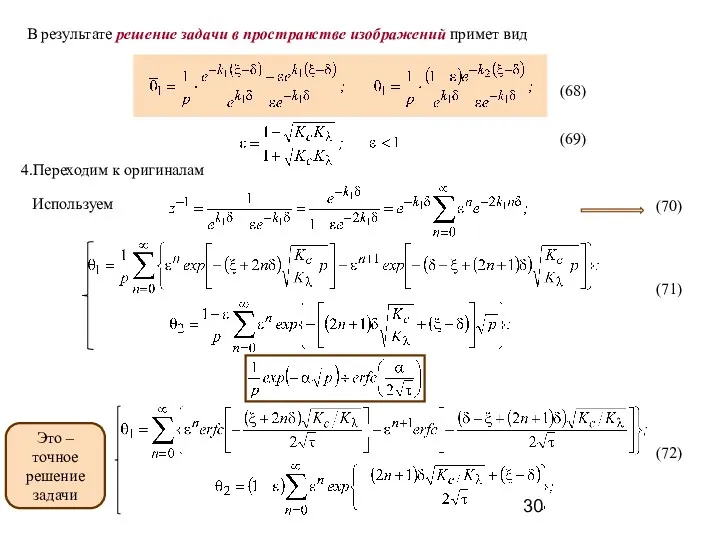
- 32. Параметр , входящий в решение, можно трактовать как термическую толщину покрытия. Это отношение реальной толщины покрытия
- 33. Задача с неидеальным тепловым контактом Неидеальный тепловой контакт может быть связан с шероховатостью поверхностей; процессами газификации…
- 35. Скачать презентацию






















 Истечение жидкости из отверстий и насадков. Насосы. Гидродинамика
Истечение жидкости из отверстий и насадков. Насосы. Гидродинамика Основы молекулярно-кинетической теории. Масса молекул. Количество вещества
Основы молекулярно-кинетической теории. Масса молекул. Количество вещества Солнечный парус
Солнечный парус Система параллельных сил и пар
Система параллельных сил и пар Потенциометрия. Электродты потенциал
Потенциометрия. Электродты потенциал Беріліс механизмдерді графикалық әдіспен кинематикалық талдау
Беріліс механизмдерді графикалық әдіспен кинематикалық талдау Ремонт компьютеров и бытовой техники в Киеве
Ремонт компьютеров и бытовой техники в Киеве Урок Атмосферное давление
Урок Атмосферное давление Інерціальні системи відліку. Перший закон Ньютона
Інерціальні системи відліку. Перший закон Ньютона Двигатель Cummins ISF 2.8
Двигатель Cummins ISF 2.8 Практическая работа. Изучение машин и оборудования для расчистки озеленяемых территорий
Практическая работа. Изучение машин и оборудования для расчистки озеленяемых территорий Механізація приготування кормових сумішей
Механізація приготування кормових сумішей Радиационный контроль
Радиационный контроль Давление. Единицы давления (7 класс)
Давление. Единицы давления (7 класс) Напряженность магнитного поля
Напряженность магнитного поля Давление твердых тел, жидкостей и газов. Своя игра
Давление твердых тел, жидкостей и газов. Своя игра Движение под действием силы тяжести. Решение задач
Движение под действием силы тяжести. Решение задач Неравномерное движение. Скорость
Неравномерное движение. Скорость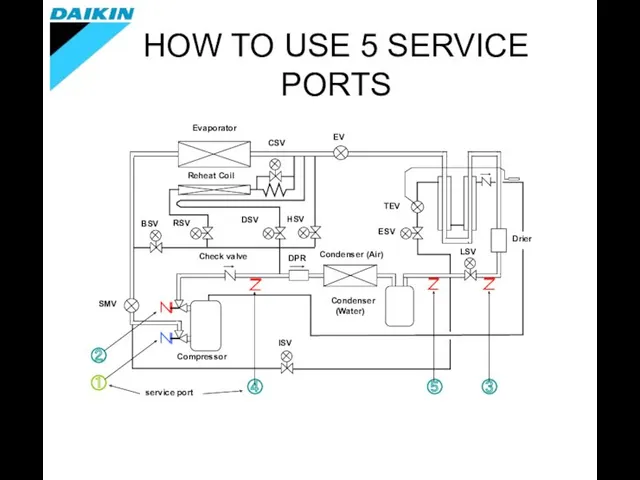 How to use 5 service ports
How to use 5 service ports Обертальний рух в нашому житті
Обертальний рух в нашому житті Приборы для измерения давления
Приборы для измерения давления Электрооборудование источников энергии, электрических сетей и промышленных предприятий
Электрооборудование источников энергии, электрических сетей и промышленных предприятий Строительная механика. Теория определения перемещений деформируемых систем. (Часть 1. Лекция 1)
Строительная механика. Теория определения перемещений деформируемых систем. (Часть 1. Лекция 1) Методи дослідження наносистем: спектроскопічні та дифракційні методи
Методи дослідження наносистем: спектроскопічні та дифракційні методи Строительная механика. Методы определения силовых факторов в деформируемых системах
Строительная механика. Методы определения силовых факторов в деформируемых системах Турбулентность. Введение
Турбулентность. Введение Теплообменные аппараты
Теплообменные аппараты Связь между напряженностью электростатического поля и разностью потенциалов. Эквипотенциальные поверхности
Связь между напряженностью электростатического поля и разностью потенциалов. Эквипотенциальные поверхности