Строительная механика. Теория определения перемещений деформируемых систем. (Часть 1. Лекция 1) презентация
Содержание
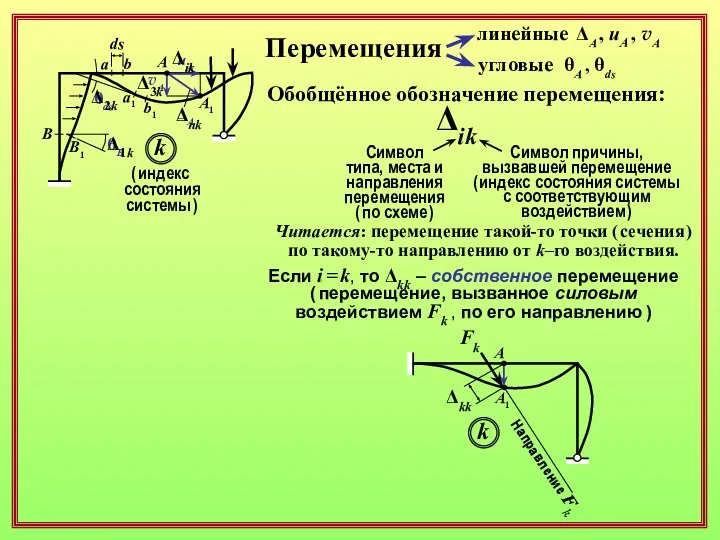
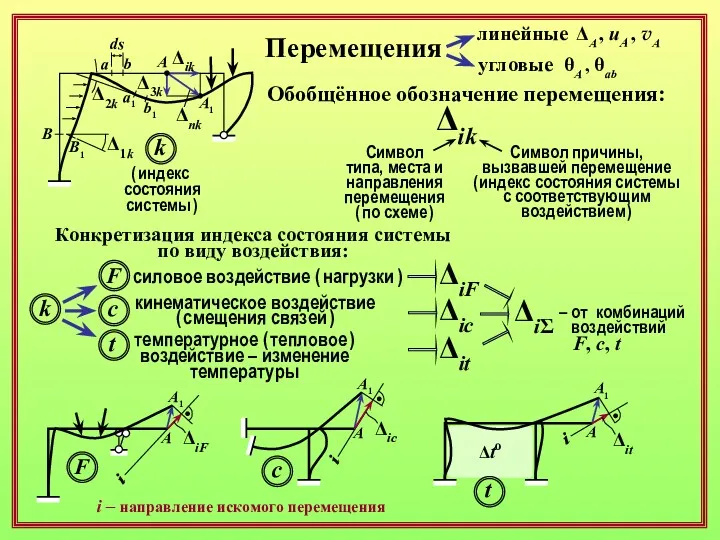
- 2. Перемещения a a1 b b1 A A1 ds B1 B θB θds ΔA uA vA линейные
- 3. Перемещения a a1 b b1 A A1 ds B1 B линейные угловые ΔA , uA ,
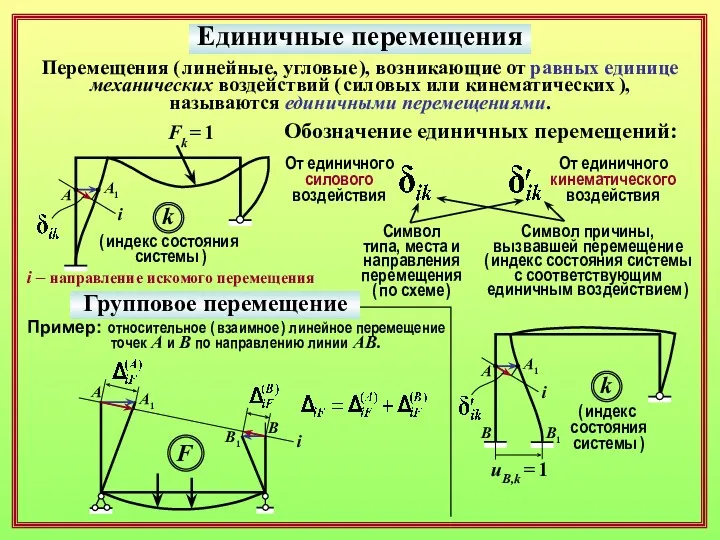
- 4. Единичные перемещения Обозначение единичных перемещений: Символ типа, места и направления перемещения ( по схеме ) Символ
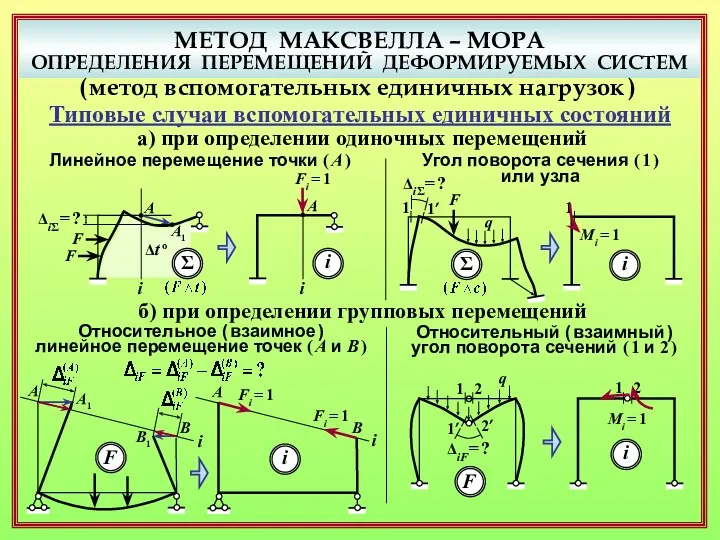
- 5. МЕТОД МАКСВЕЛЛА – МОРА ОПРЕДЕЛЕНИЯ ПЕРЕМЕЩЕНИЙ ДЕФОРМИРУЕМЫХ СИСТЕМ ( метод вспомогательных единичных нагрузок ) J.C. Maxwell
- 6. МЕТОД МАКСВЕЛЛА – МОРА ОПРЕДЕЛЕНИЯ ПЕРЕМЕЩЕНИЙ ДЕФОРМИРУЕМЫХ СИСТЕМ ( метод вспомогательных единичных нагрузок ) Правило задания
- 7. МЕТОД МАКСВЕЛЛА – МОРА ОПРЕДЕЛЕНИЯ ПЕРЕМЕЩЕНИЙ ДЕФОРМИРУЕМЫХ СИСТЕМ ( метод вспомогательных единичных нагрузок ) Типовые случаи
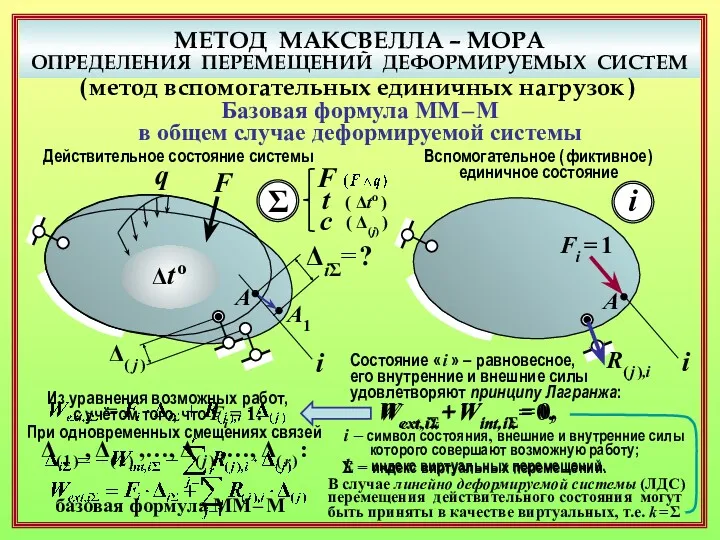
- 8. МЕТОД МАКСВЕЛЛА – МОРА ОПРЕДЕЛЕНИЯ ПЕРЕМЕЩЕНИЙ ДЕФОРМИРУЕМЫХ СИСТЕМ ( метод вспомогательных единичных нагрузок ) Базовая формула
- 9. ВОЗМОЖНАЯ И ДЕЙСТВИТЕЛЬНАЯ РАБОТА ВНЕШНИХ И ВНУТРЕННИХ СИЛ. ПОТЕНЦИАЛЬНАЯ ЭНЕРГИЯ ДЕФОРМАЦИИ Возможной работой внешних ( внутренних
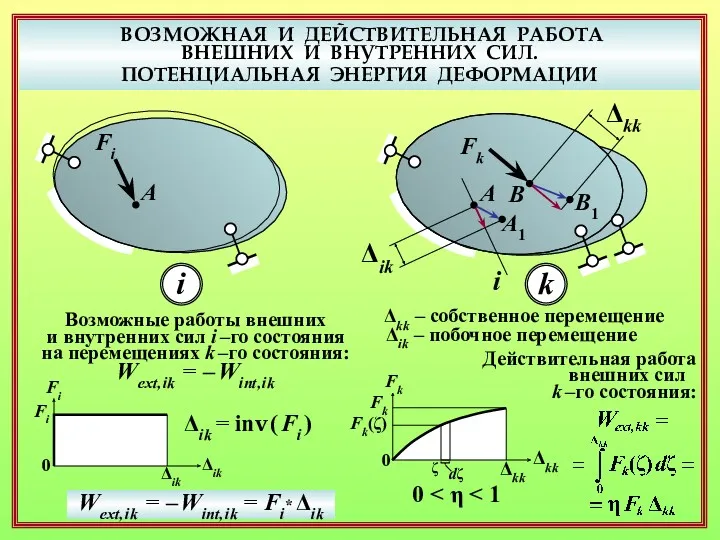
- 10. ВОЗМОЖНАЯ И ДЕЙСТВИТЕЛЬНАЯ РАБОТА ВНЕШНИХ И ВНУТРЕННИХ СИЛ. ПОТЕНЦИАЛЬНАЯ ЭНЕРГИЯ ДЕФОРМАЦИИ A Fi i i k
- 11. ВОЗМОЖНАЯ И ДЕЙСТВИТЕЛЬНАЯ РАБОТА ВНЕШНИХ И ВНУТРЕННИХ СИЛ. ПОТЕНЦИАЛЬНАЯ ЭНЕРГИЯ ДЕФОРМАЦИИ A Fi i i k
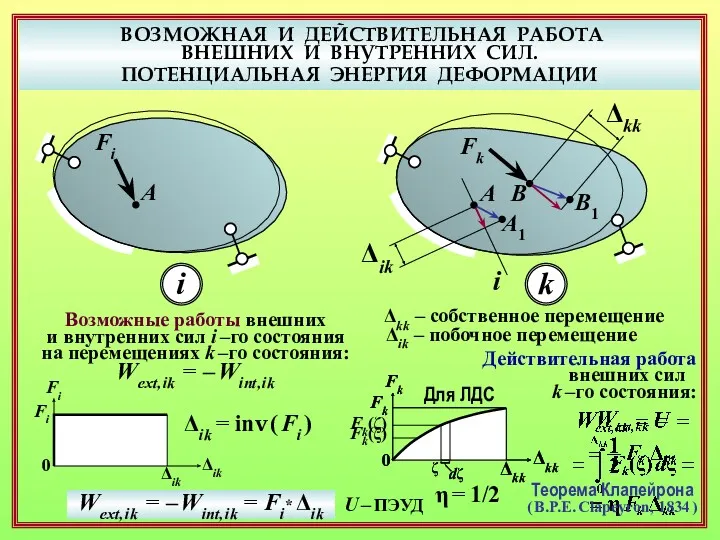
- 12. ВОЗМОЖНАЯ И ДЕЙСТВИТЕЛЬНАЯ РАБОТА ВНЕШНИХ И ВНУТРЕННИХ СИЛ. ПОТЕНЦИАЛЬНАЯ ЭНЕРГИЯ ДЕФОРМАЦИИ A Fi i i k
- 13. ВОЗМОЖНАЯ И ДЕЙСТВИТЕЛЬНАЯ РАБОТА ВНЕШНИХ И ВНУТРЕННИХ СИЛ. ПОТЕНЦИАЛЬНАЯ ЭНЕРГИЯ ДЕФОРМАЦИИ A Fi i i k
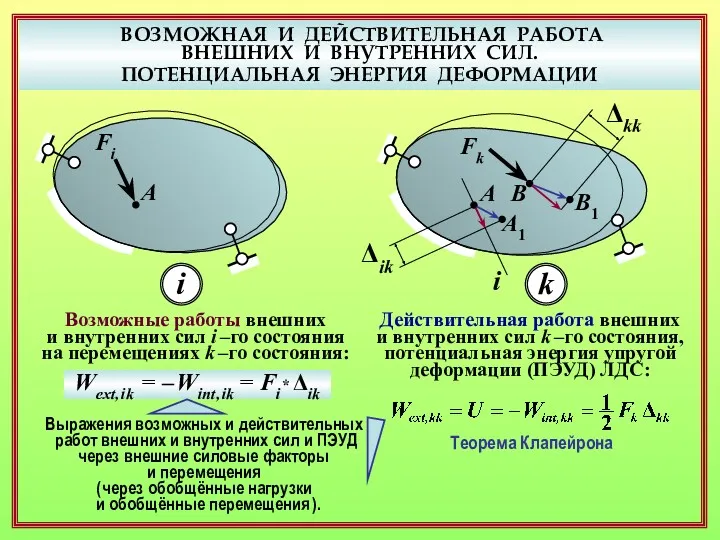
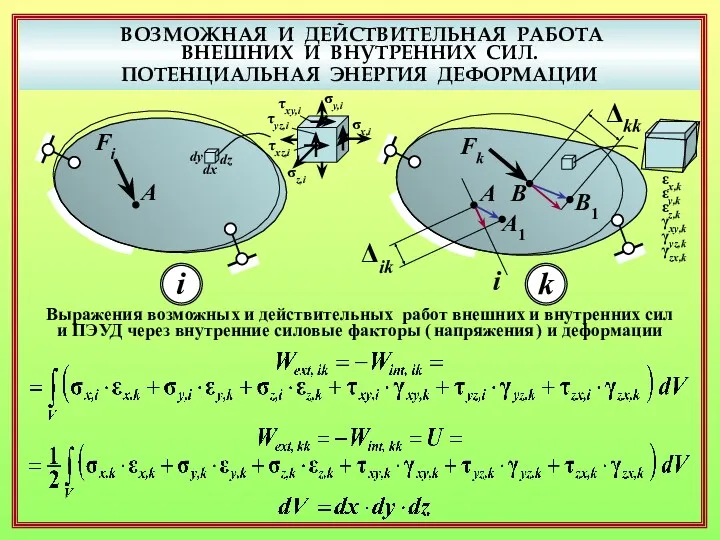
- 14. ВОЗМОЖНАЯ И ДЕЙСТВИТЕЛЬНАЯ РАБОТА ВНЕШНИХ И ВНУТРЕННИХ СИЛ. ПОТЕНЦИАЛЬНАЯ ЭНЕРГИЯ ДЕФОРМАЦИИ Выражения возможных и действительных работ
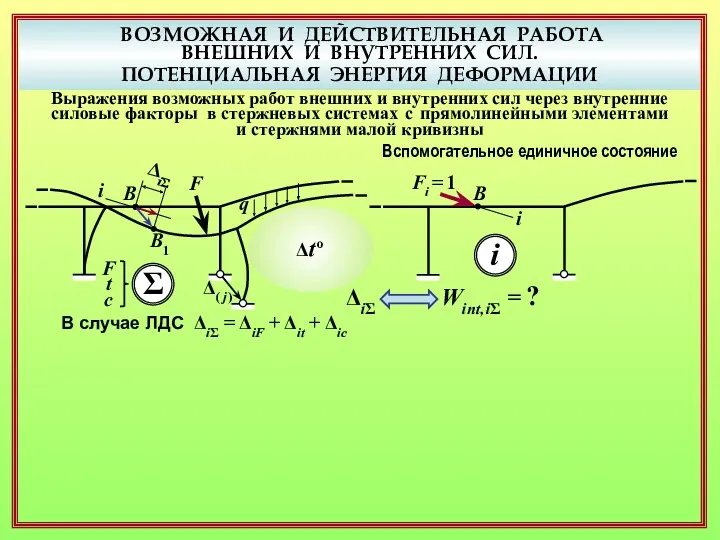
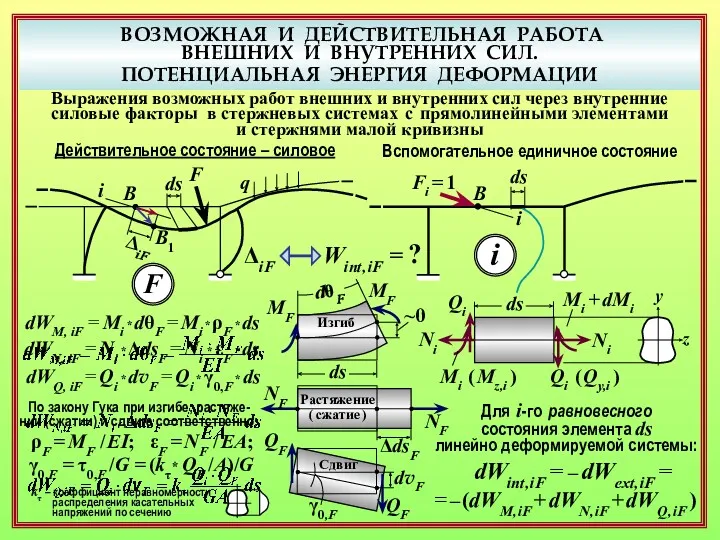
- 15. ВОЗМОЖНАЯ И ДЕЙСТВИТЕЛЬНАЯ РАБОТА ВНЕШНИХ И ВНУТРЕННИХ СИЛ. ПОТЕНЦИАЛЬНАЯ ЭНЕРГИЯ ДЕФОРМАЦИИ Выражения возможных работ внешних и
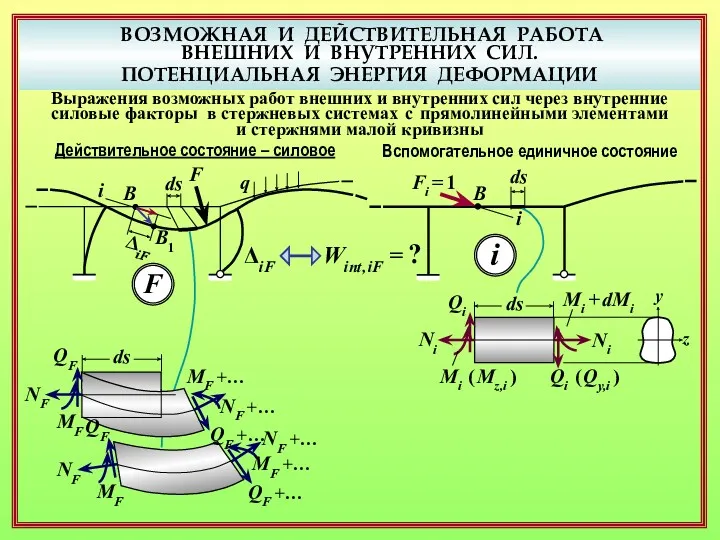
- 16. ВОЗМОЖНАЯ И ДЕЙСТВИТЕЛЬНАЯ РАБОТА ВНЕШНИХ И ВНУТРЕННИХ СИЛ. ПОТЕНЦИАЛЬНАЯ ЭНЕРГИЯ ДЕФОРМАЦИИ Выражения возможных работ внешних и
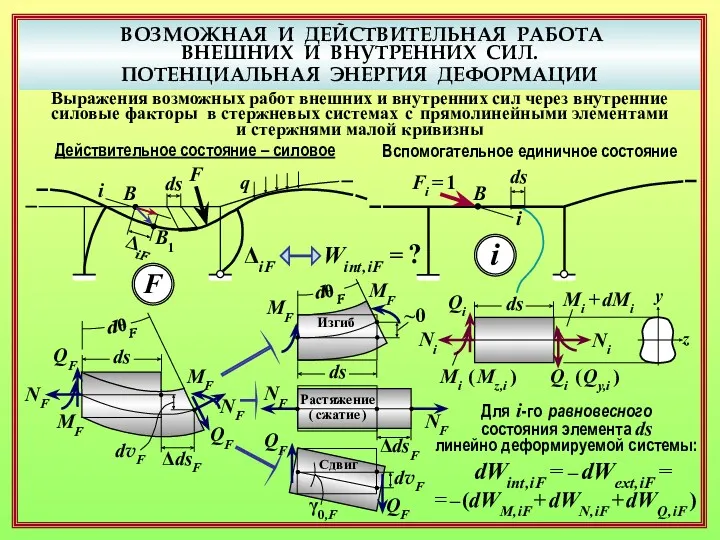
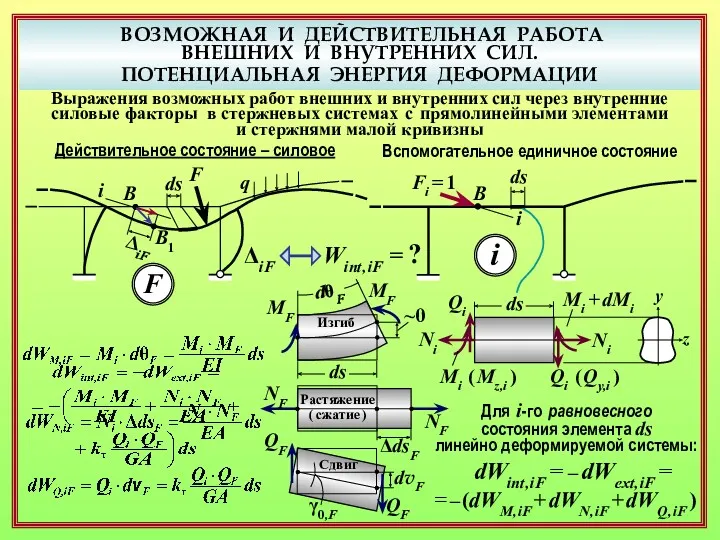
- 17. ВОЗМОЖНАЯ И ДЕЙСТВИТЕЛЬНАЯ РАБОТА ВНЕШНИХ И ВНУТРЕННИХ СИЛ. ПОТЕНЦИАЛЬНАЯ ЭНЕРГИЯ ДЕФОРМАЦИИ Выражения возможных работ внешних и
- 18. ВОЗМОЖНАЯ И ДЕЙСТВИТЕЛЬНАЯ РАБОТА ВНЕШНИХ И ВНУТРЕННИХ СИЛ. ПОТЕНЦИАЛЬНАЯ ЭНЕРГИЯ ДЕФОРМАЦИИ Выражения возможных работ внешних и
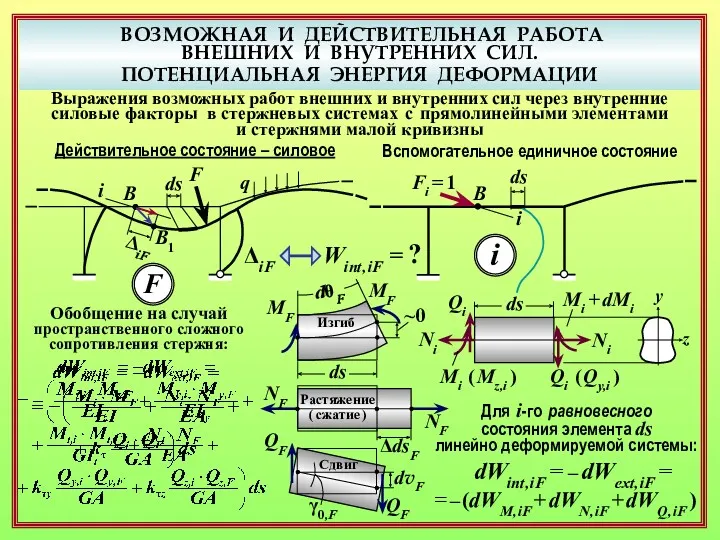
- 19. ВОЗМОЖНАЯ И ДЕЙСТВИТЕЛЬНАЯ РАБОТА ВНЕШНИХ И ВНУТРЕННИХ СИЛ. ПОТЕНЦИАЛЬНАЯ ЭНЕРГИЯ ДЕФОРМАЦИИ Выражения возможных работ внешних и
- 20. ВОЗМОЖНАЯ И ДЕЙСТВИТЕЛЬНАЯ РАБОТА ВНЕШНИХ И ВНУТРЕННИХ СИЛ. ПОТЕНЦИАЛЬНАЯ ЭНЕРГИЯ ДЕФОРМАЦИИ Выражения возможных работ внешних и
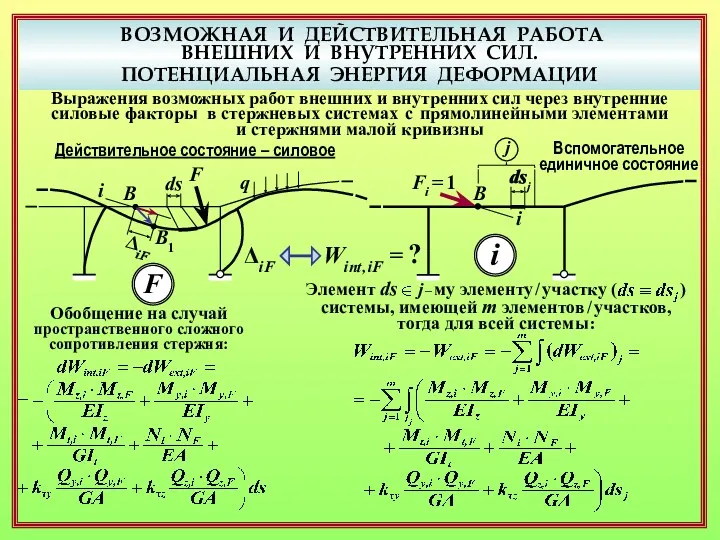
- 21. ВОЗМОЖНАЯ И ДЕЙСТВИТЕЛЬНАЯ РАБОТА ВНЕШНИХ И ВНУТРЕННИХ СИЛ. ПОТЕНЦИАЛЬНАЯ ЭНЕРГИЯ ДЕФОРМАЦИИ Выражения возможных работ внешних и
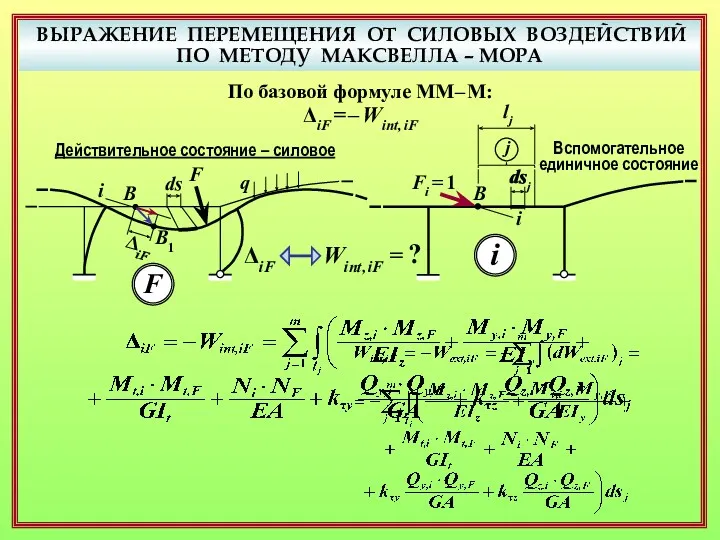
- 22. ВЫРАЖЕНИЕ ПЕРЕМЕЩЕНИЯ ОТ СИЛОВЫХ ВОЗДЕЙСТВИЙ ПО МЕТОДУ МАКСВЕЛЛА – МОРА F q В В1 i ds
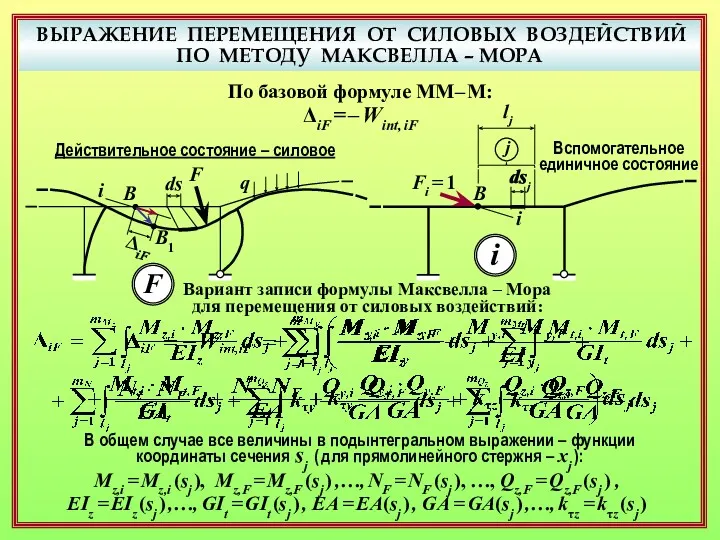
- 23. ВЫРАЖЕНИЕ ПЕРЕМЕЩЕНИЯ ОТ СИЛОВЫХ ВОЗДЕЙСТВИЙ ПО МЕТОДУ МАКСВЕЛЛА – МОРА F q В В1 i ds
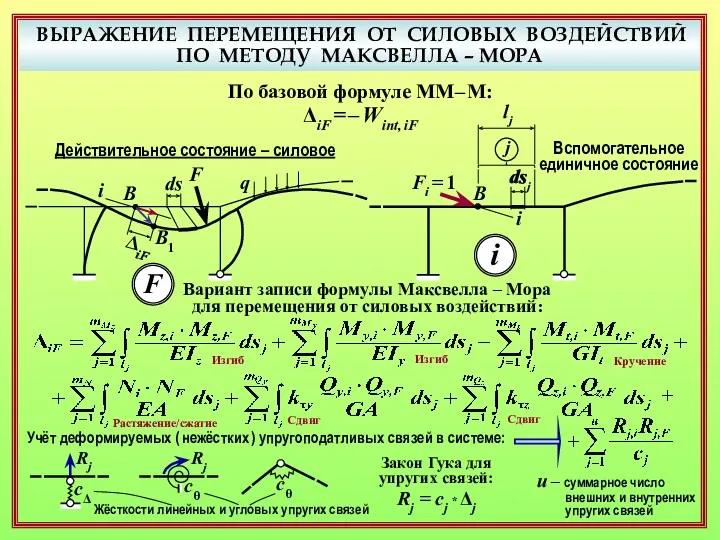
- 24. ВЫРАЖЕНИЕ ПЕРЕМЕЩЕНИЯ ОТ СИЛОВЫХ ВОЗДЕЙСТВИЙ ПО МЕТОДУ МАКСВЕЛЛА – МОРА F q В В1 i ds
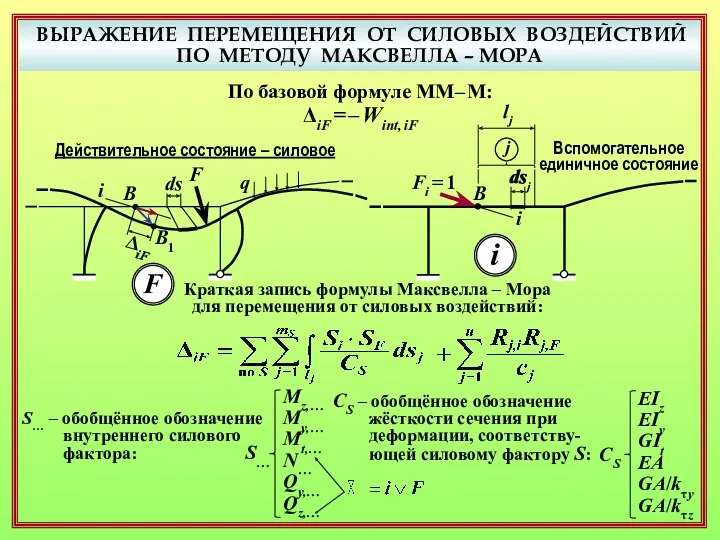
- 25. ВЫРАЖЕНИЕ ПЕРЕМЕЩЕНИЯ ОТ СИЛОВЫХ ВОЗДЕЙСТВИЙ ПО МЕТОДУ МАКСВЕЛЛА – МОРА F q В В1 i ds
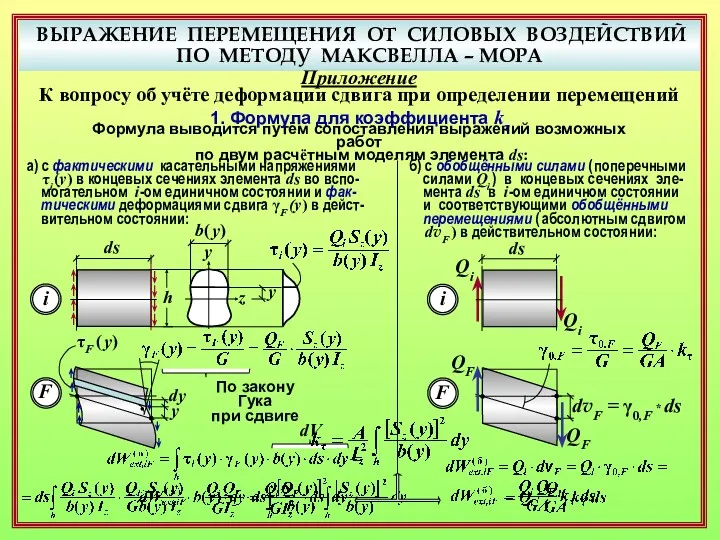
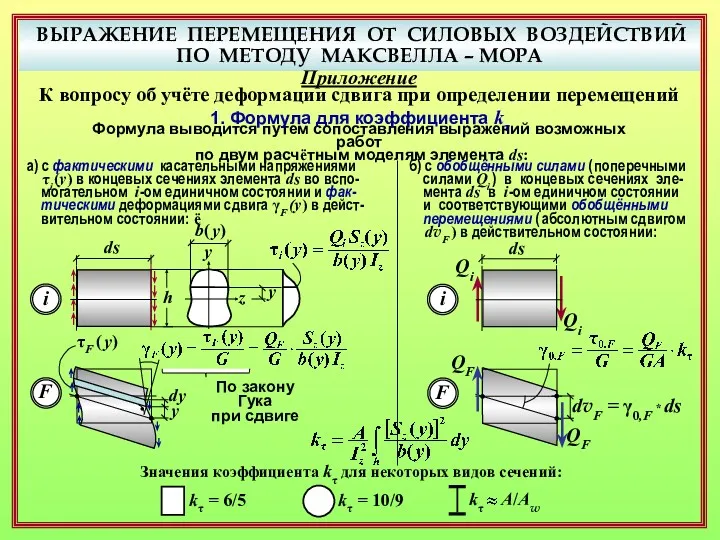
- 26. ВЫРАЖЕНИЕ ПЕРЕМЕЩЕНИЯ ОТ СИЛОВЫХ ВОЗДЕЙСТВИЙ ПО МЕТОДУ МАКСВЕЛЛА – МОРА Приложение К вопросу об учёте деформации
- 27. ВЫРАЖЕНИЕ ПЕРЕМЕЩЕНИЯ ОТ СИЛОВЫХ ВОЗДЕЙСТВИЙ ПО МЕТОДУ МАКСВЕЛЛА – МОРА Приложение К вопросу об учёте деформации
- 28. ВЫРАЖЕНИЕ ПЕРЕМЕЩЕНИЯ ОТ СИЛОВЫХ ВОЗДЕЙСТВИЙ ПО МЕТОДУ МАКСВЕЛЛА – МОРА Приложение К вопросу об учёте деформации
- 29. К о н т р о л ь н ы е в о п р о
- 31. Скачать презентацию






 Ядерные энергетические установки
Ядерные энергетические установки Естественные и искусственные освещения
Естественные и искусственные освещения Обобщающий урок-игра по физике, 9 класс
Обобщающий урок-игра по физике, 9 класс Ультразвук, источники ультразвука
Ультразвук, источники ультразвука Винтовые передачи. Достоинства и недостатки
Винтовые передачи. Достоинства и недостатки Презентация к уроку Использование физических понятий, величин и законов при решении задач на расчёт средней скорости
Презентация к уроку Использование физических понятий, величин и законов при решении задач на расчёт средней скорости Микроскоп – знакомство, создание, опыты
Микроскоп – знакомство, создание, опыты Электрические измерения и приборы
Электрические измерения и приборы Соединения деталей. Резьбы и их типы. Алгоритм построения чертежа
Соединения деталей. Резьбы и их типы. Алгоритм построения чертежа Работа, мощность, энергия
Работа, мощность, энергия квантовая физика
квантовая физика Оптоэлектронные и квантовые приборы и устройства. Светодиоды
Оптоэлектронные и квантовые приборы и устройства. Светодиоды Intelligent energy storage
Intelligent energy storage Действие магнитного поля на движущуюся заряженную частицу. Сила Лоренца
Действие магнитного поля на движущуюся заряженную частицу. Сила Лоренца Процесс сборки-сварки корпуса емкости дистиллятора Е-201
Процесс сборки-сварки корпуса емкости дистиллятора Е-201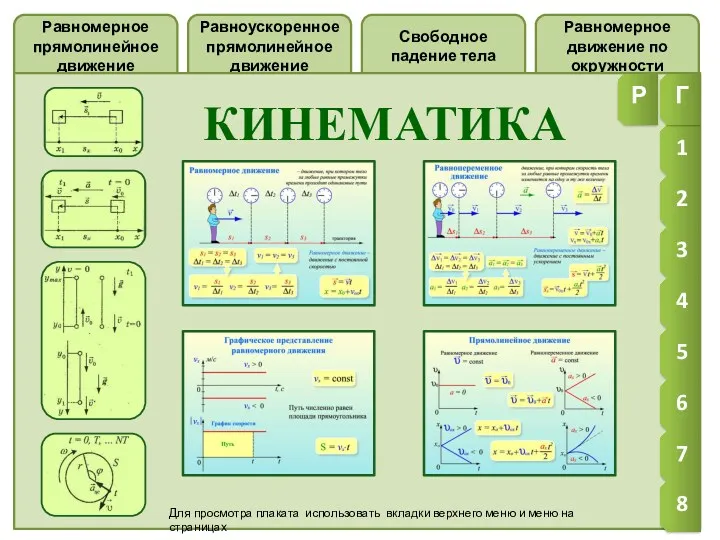 Кинематика. Равномерное прямолинейное движение
Кинематика. Равномерное прямолинейное движение Презентация к уроку по теме Сила тяжести
Презентация к уроку по теме Сила тяжести Уравнение состояния идеального газа. Газовые законы
Уравнение состояния идеального газа. Газовые законы Измерение температуры
Измерение температуры Однофазная цепь с последовательным соединением электроприемников
Однофазная цепь с последовательным соединением электроприемников Опыты по физике
Опыты по физике Механические свойства металлов
Механические свойства металлов Физические основы механики. Кинематика материальной точки
Физические основы механики. Кинематика материальной точки Естественные и искусственные стекла
Естественные и искусственные стекла Архимедова сила
Архимедова сила Машина ремонтно-эвакуационная колесная легкая РЭМ-КЛ
Машина ремонтно-эвакуационная колесная легкая РЭМ-КЛ Diamond DA42 Twin Star — лёгкий многоцелевой самолёт
Diamond DA42 Twin Star — лёгкий многоцелевой самолёт работа и мощность эл.тока
работа и мощность эл.тока